pg_met_pr2

ВСТУП

У цих методичних вказівках наведені приклади розв’язання найбільш типових задач із розділу “Молекулярна фізика та термодинаміка”, а також подані задачі для самостійного розв’язання. Автори мають на меті сформувати у студентів методологію розв’язання задач, допомогти засвоїти фізичні закони, навчити деяких математичних прийомів, що широко використовуються у фізиці. При роботі над кожною темою варто дотримуватися таких рекомендацій:

1Детально опрацювати теоретичний матеріал за підручником з курсу загальної фізики (наприклад, [1-2]).

2Уважно вивчити приклади розв’язання розібраних задач з даної теми. З’ясувати всі не зрозумілі для себе моменти у розв’язанні задачі, записати розв’язки в зошит. За необхідності ще раз звернутися до підручника для більш глибокого опрацювання теоретичного матеріалу або ж звернутися за консультацією до викладача. Пам’ятайте, необхідно домогтися повного розуміння розв’язання наведених задач. Перехід до самостійного розв’язання задач варто проводити тільки після повного розуміння прикладів поданих у даній темі.

3Перейти до самостійного розв’язання задач даної теми. При

б) з’ясувати сутність процесів, про які йдеться мова в задачі; в) установити закони, які слід використати для розв’язання задачі, записати відповідні рівняння; г) провести математичні перетворення, отримати розв’язок у загальному вигляді, шукана величина повинна бути виражена через величини, що наведені в умові задачі; д) виконати аналіз отриманого розв’язку щодо його відповідності фізичному змісту.

Пам’ятайте! Щоб зрозуміти, як розв’язується задача, від вас потрібні серйозні міркування. Бажаємо Вам успіху!

4

ТЕМА 1 РІВНЯННЯ ГАЗУ. ПРОЦЕСИ

Приклад 1.1

Балон об’ємом 20 л містить суміш водню й азоту при температурі 270С і тиску 25 атм. Маса суміші газів – 0,3 кг. Визначити масу водню, яка міститься в балоні.

абсолютну температуру газів.

5

праву й ліву частини цього співвідношення замість символів фізичних величин підставимо їх одиниці вимірювання.

Зрозуміло, що [m1] =кг.

Тобто кг = кг . Таким чином, розрахункова формула (5) дає правильні одиниці вимірювання.

2 Запишемо фізичні величини, що входять в розрахункову формулу (5), в одиницях СІ й виконаємо обчислення:

3 Проведемо дослідження розрахункової формули у граничних випадках.

Розглянемо уявний випадок, коли маса однієї молекули газу, який позначаємо індексом «1», буде дорівнювати нулю. Тоді і їх молярна маса також буде дорівнювати нулю m1 ® 0. З

фізичних міркувань випливає, що в цьому випадку будь-яка кількість молекул цього сорту газу буде мати масу таку, що

7

Приклад 1.2

Швидкість відкачування роторного масляного насоса Q =1,5×10−4 м3/с. Який час τ потрібен для того, щоб посудину

місткістю V = 5 л відкачати від нормального повітряного тиску до тиску p = 1,33 Па?

Примітка. Швидкістю відкачування називають об’єм газу, який відкачується за одиницю часу. Зазначимо, що цей об’єм вимірюється при тиску газу в даний момент часу.

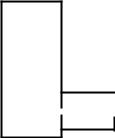
V ,

dV1 = Qdt

K1 K 2

Рисунок 1.1

Нехай у деякий момент часу t в посудині об’ємом V міститься повітря, що характеризується тиском p та масою m .

З часом завдяки роботі насоса маса газу m в посудині зменшується. Через це зменшується і тиск p газу в посудині.

Насос працює таким чином. За малий час dt через систему клапанів K1 та K2 (див. рис. 1.1) з посудини видаляється газ, що міститься в об’ємі dV1 = Qdt . Зрозуміло, що зменшення маси

8

газу в посудині dm дорівнює масі газу, який міститься в об’ємі dV1 . Це зменшення газу дорівнює

dm = −ρdV1 = −ρQdt . (1)

Знак «–» у цій формулі означає, що маса газу в посудині об’ємом V зменшується, ρ - густина газу в системі в даний момент часу.

Цю густину газу можна знайти за допомогою рівняння Менделєєва-Клапейрона

зменшенням маси газу також знаходимо за допомогою рівняння Менделєєва-Клапейрона

Інтегруємо праву і ліву частини співвідношення (4) і знаходимо шуканий час τ :

9

Аналіз отриманого результату

1 Перевіримо, чи дає розрахункова формула (5) правильну одиницю вимірювання шуканої фізичної величини. Для цього в праву й ліву частини цього співвідношення замість символів фізичних величин підставимо їх одиниці вимірювання.

Зрозуміло, що [τ] = кг.

Тобто с = с . Таким чином, розрахункова формула (5) дає правильні одиниці вимірювання.

2 Запишемо фізичні величини, що входять в розрахункову формулу (5), в одиницях СІ й виконаємо обчислення:

3 Проведемо дослідження розрахункової формули у граничних випадках.

Розглянемо випадок, коли швидкість відкачування насоса буде наближатись до нуля Q → 0 . У цій ситуації відкачування

практично не буде відбуватись. Тобто час відкачування буде

Отже, розрахункова формула (5) не суперечить фізичним міркуванням.

Відповідь: t = VQ ln pp0 =374 с.

10