Эффекты, связанные с относительным движением фаз.

Рассмотрим теперь эффекты, связанные с относительным движением фаз, а следовательно, и с их взаимодействием. Теоретическое описание таких эффектов будет, очевидно, существенно зависеть от того, используется ли при этом простая односкоростная модель или реальная двухскоростная модель (как выше).

Прежде всего сила межфазового взаимодействия в (8) отличается от вычисленной в том отношении, что вместо скорости суспензии (или с) в (8) фигурирует средняя скорость непрерывной фазы(или). Это совершенно не существенно при описании движения суспензии как целого, но весьма важно при анализе явлений типа оседания суспензий в каналах, отстойниках и т. д. Действительно, вычислим, например, скорость седиментации частицв поле тяжестипри условии, что суспензия в целом неподвижна, т. е.. Из (2) имеем в данном случае,и уравнение сохранения импульса дисперсной фазы из (1) дает:

(13)

Отсюда и из определения в (2) ив (12) получаем:

(14)

Где - стоксова скорость оседания частицы в чистой непрерывной фазе, плотность и вязкость в которой равныисоответственно.

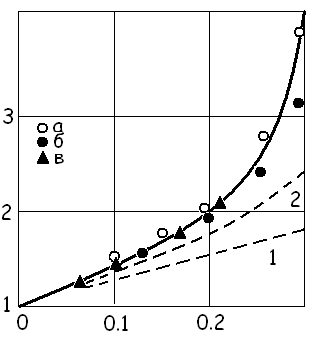
Рис.1.

Зависимость относительной вязкости суспензии от ее объёмной концентрации.

Сплошная кривая – формула (12), штриховые – формулы Эйнштейна (1) и

Бетчелора-Грина (13), а – данные (10), б – (11), в – (12).

Рис.2.

Зависимость относительной скорости седиментации от объёмной концентрации суспензии; штриховая – формула Бетчелора, 1 – экспериментальные данные (14), 2 – (15).

На рис.2 сравнивается формула (14) с экспериментами. Здесь же показана кривая, следующая из опыта. Видно, что согласие между теорией и опытом достаточно хорошее вплоть до значений , равных 0,20-0,25.

Укажем смысл отдельных членов в (8). Первый член описывает силу вязкого воздействия окружающей среды на частицы в единице объёма суспензии; при этом роль вязкости среды играет эффективная вязкость суспензии , а роль относительной скорости – истинная скорость межфазового скольжения. Второй член представляет собой эффективную вязкость Факсена, также определяемую при помощи вязкости. Наконец, третий член в (8) описывает эффективную силу плавучести (архимедову силу), обусловленную как внешним полем массовых сил, так и полем инерционных сил; при этом в качестве плотности внешней среды фигурирует средняя плотность суспензии.

Отметим, что дискуссия о том, каким образом правильно записать отдельные члены в выражении для силы межфазового взаимодействия, в частности, связанные с градиентом давления в невозмущенном потоке, продолжается до сих пор, причем проводится различие между компонентами этого градиента, вызванными гидростатическими и гидродинамическими причинами. Формула (8) позволяет завершить эту дискуссию применительно к установившимся потокам с мелкими частицами.

Укажем, что имеется ряд проблем, в котором правильный учет составляющих силы взаимодействия оказывается важным не только в количественном, но и в качественном отношении. Так, например, введение в указанную силу члена серьёзно изменяет картину инерционного осаждения частиц суспензии на обтекаемое ею тело по сравнению с картиной, предсказываемой в случае, если такой член не учитывается. В действительности вместо члена св (8) фигурирует член, пропорциональный, и хотя последняя величина может быть выражена через другие динамические переменные при помощи уравнений движения, его окончательное выражение все же отличается.

До их пор рассматривались уравнения сохранения массы и импульса. В ряде случаев важно исследовать также влияние составляющих тензора эффективных напряжений, зависящих от угловых скоростей вращения частиц, а также уравнения сохранения момента импульса фаз. В последних фигурируют две величины, также выражающиеся через интегралы по поверхности пробной частицы от воздействующих на ней напряжений, - средний момент межфазового взаимодействия и псевдотензор средних моментных напряжений. Из решения задачи (6) после вычислений получаем:

(15)

а также

(16)

Здесь – антисимметричный альтернирующий тензор Леви-Чивиты, апсевдотензор скоростей деформаций, построенный по полю псевдовектора. Очевидно, что с принятой точностью.