Курсовые / Вязкость и теплопров. дисперсной среды

ОБ. ЭФФЕКТИВНОЙ ВЯЗКОСТИ И ТЕПЛОПРОВОДНОСТИ ДИСПЕРСНОЙ СРЕДЫ

Вычеслены коэффициенты эффективной вязкости и теплопроводности концентрированных дисперсных сред со сферическими частицами при различных видах бинарной функции распределения.

Рассмотрим изотропную дисперсную среду, состоящую из непрерывной фазы и распределенных в ней случайным образом твердых сферических частиц радиуса а, объемная концентрация которых постоянна. В общем случае обе фазы могут быть подвижны и иметь различные скорости.

Ниже для этой системы, удовлетворяющей всем основным условиям применимости метода [1] и на его основе, вычисляются коэффициенты эффективной вязкости и теплопроводности, характеризующие соответст­венно перенос импульса и тепла. Эти коэффициенты входят в уравнения, описывающие процессы переноса для всей среды в целом.

Перенос импульса. Пусть дисперсная система представляет собой суспензию, непрерывная фаза которой есть ньютоновская жидкость с вязкостью μ0 и плотностью d0. Числа Рейнольдса, характеризующие как локальный перенос вблизи частицы, так и движение суспензии в целом, считаем малыми по сравнению с единицей. Тогда стационарное движение суспензии в целом в лабораторной системе координат r описывается уравнениями сохранения массы u импульса [1]

(1)

Коэффициент эффективной вязкости μ, входящий в (1), определяется из условия самосогласованности [1]

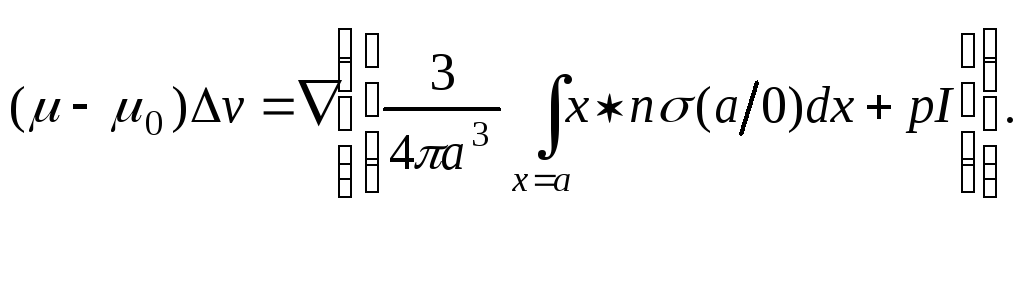(2)

Здесь σ(а/0) — тензор условных средних напряжений, действующих на поверхности х = а выделенной («пробной») частицы, который вычисляется из решения задачи об обтекании этой частицы какой-либо фиктивной гомогенной средой. Реологические свойства этой среды на удаление от поверхности частицы совпадают со свойствами суспензии в целом, а на расстояниях, сравнимых с радиусом частицы, зависят от расстояния.

Отметим, что в рассматриваемом случае пространственные производные скоростей в лабораторной и конвективной системе координат х, связанной с центром пробной частицы, совпадают.

При определении эффективной вязкости суспензии односкоростная модель, используемая здесь, и двухскоростная [2] дают одинаковые ре­зультаты. Однако при вычислении скорости оседания суспензии, что не входит в рамки данной работы, необходимо пользоваться двухскоростной моделью.

Пусть плотности фаз совпадают d1=d0, тогда поля возмущений ско-

рости v^{^} и давления p^{^}, вносимые «пробной» частицей в двухфазный поток, определяются из решения задачи [1, 2]

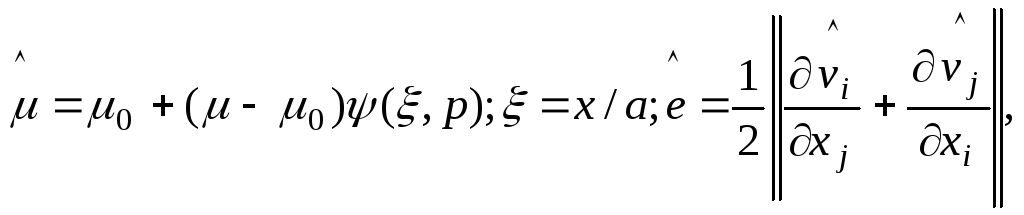(3)

где ê — тензор скоростей деформаций, a ψ (ξ, p) характеризует особен­ности распределения частиц в ближайшей окрестности выделенной части­цы. Можно показать, что функция ψ (ξ, p) однозначно определяется би­нарной функцией распределения (БФР)

(4)

где n(х/0) — условная счетная концентрация частиц.

Используя центральную симметрию, из (4) получаем

(5)

Для замыкания задачи (3) необходимо знать БФР, входящую в (5). Определение этой функции представляет собой сложную задачу стати­стической физики и возможно только в простых случаях.

Для непроницаемых частиц, расположенных случайным образом, та­кая задача была решена в [3] в суперпозиционном приближении, где было показано, что БФР представляет собой осциллирующую затухаю­щую функцию, амплитуда и степень затухания которой зависят от объем­ной концентрации дисперсной фазы. Результаты [3] были получены в предположении о хаотичности расположения частиц.

Решение задачи еще более осложняется для суспензии, так как бинар­ная функция распределения зависит от параметров течения суспензии, которые в свою очередь зависят от нее самой. Следовательно, для опре­деления искомой функции необходимо совместно решать уравнения типа (3) и уравнения, описывающие поведение БФР. Для весьма разреженной суспензии, когда можно учитывать только парные взаимодействия, та­кая задача была решена в [4]. При этом предполагалось, что суспензия участвует в линейном чисто сдвиговом движении. Полученная в [4]

БФР оказалась не зависящей от объемной концентрации дисперсной фазы. В данной работе эта функция считается заданной.

Решение задачи о пробной частице. Для решения задачи (3) исполь­зуем метод, разработанный в [5], а именно ищем решение (3) в форме рядов по базисным векторным функциям, построенным на сферических функциях

(6)

причем функции f_m, g_m, l_m зависят только от ξ и могут быть определены из системы уравнений

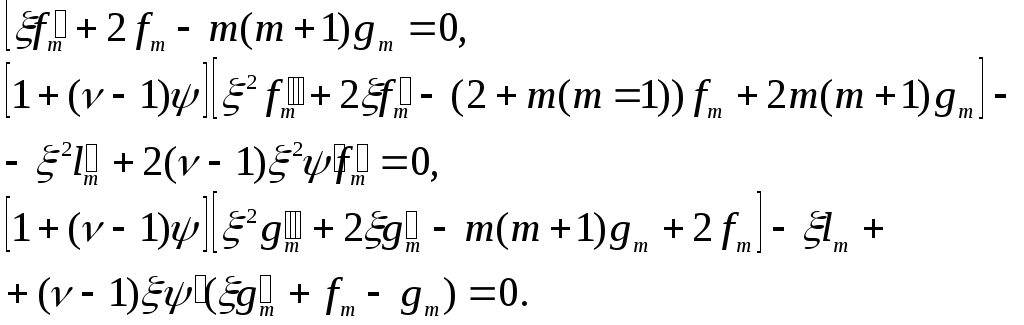(7)

Здесь штрих означает дифференцирование по ξ и введен безразмерный коэффициент эффективной вязкости v = μ / μ0

Невозмущенные поля v и р также могут быть представлены в виде рядов типа (6) с функциями F_m, G_m,L_m. Коэффициенты этих функций выражаются через значения скорости v и ее производных в точке, заня­той центром пробной частицы, и, следовательно, могут рассматриваться как заданные априори [5].

Граничные условия для (7) имеют вид

(8)

Решение задачи (7), (8) полностью определяет ряды (6) для полей возмущений и позволяет вычислить входящий в (2) интеграл, который можно представить в виде

(9)

Коэффициенты K⁽¹⁾ и K⁽²⁾ зависят от v, ρ и вида используемой функции ψ(ξ,p)

Отметим, что вследствие ортогональности сферических функций вклад в поверхностный интеграл (9) дают члены рядов (6), содержащие толь­ко s₂. Поэтому нижний индекс в дальнейшем опускаем, подразумевая, что он равен двум.

Из (2) и (9), учитывая, что, получаем уравнение,

определяющее неизвестный параметр

(10)

и полностью замыкающее задачу.

Дли численного решении (7), (8) преобразуем ее к виду

(11)

здесь z=ξ ^-1; штрих означает дифференцирование по z, а y(z) —новая функция, определяемая первым уравненным (11), При выводе граничных условий использовалось предположение, что уравнение неразрывности справедливо везде вплоть до границы.

Для получения искомой зависимости v от ρ трансцендентное относи­тельно v уравнение (10), в данном случае имеющее вид

решалось численно методом Ньютона. На каждом итерационном шаге по v для определения значений функции y и ее производной при z=1 задача (11) интегрировалась методом матричной прогонки.

Реологические свойства суспензии. Как указывалось выше, БФР од­нозначно определяет функцию. ψ (ξ, p), входящую в (3).

Если пренебречь неперекрываемостью частиц, БФР постоянна и рав­на единице на всем интервале изменения . Тогда ψ=1 при (кривая 1 рис. 1).

Такое предположение было использовано в [1] при вычислении коэф­фициента эффективной вязкости умеренно концентрированных суспен­зий и в [2] — при определении скорости седиментации таких суспензий. График полученной в [1] зависимости представлен на рис. 2 кривой 1. Учет непроницаемости частиц приводит к более сложному виду функ­ции ψ (ξ, p). Если использовать БФР в виде

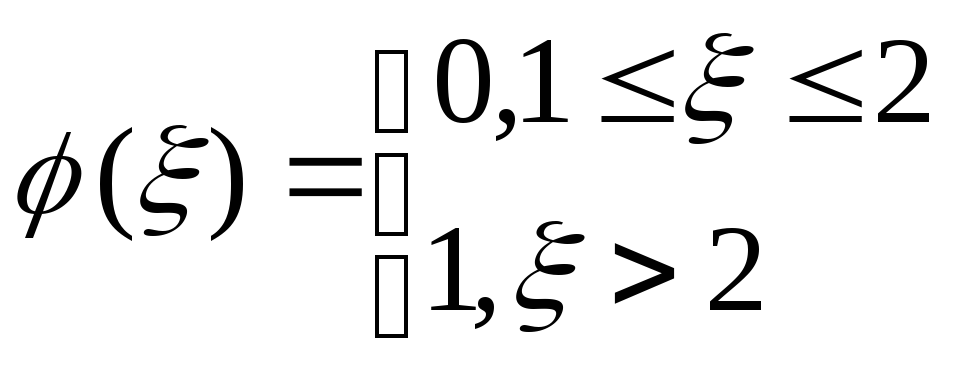
из (5) получаем

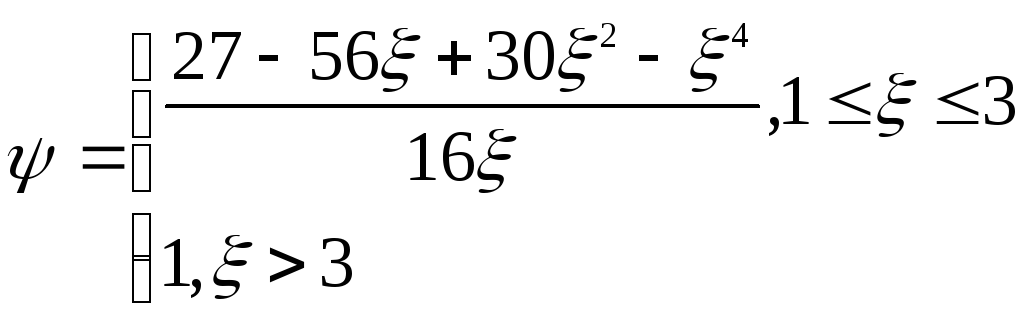(12)

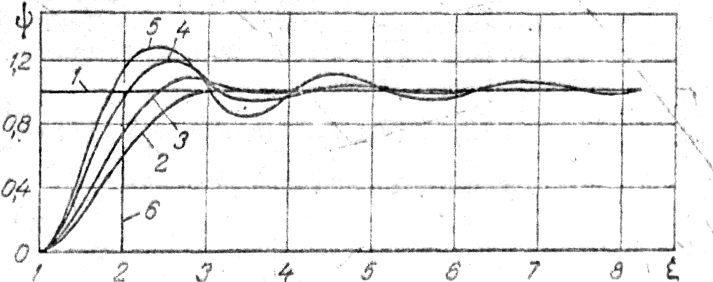
Рис, 1. Зависимость функции ψ от расстояния: 1 — модель взаимопроникающих частиц;

2 — использующая БФР в виде ступеньки; 3 —модель, использующая ВФР [3] при

р= 0,144; 4—0,353; 5 — 0,482; 6 — модель с кольцом

(рис. 1, кривая 2). Отметим, что функция ψ (ξ) из (12) не зависит от ве­ личины объемной концентрации дисперсной фазы. Полученная в резуль­тате численных расчетов с учетом (12) зависимость безразмерного коэф­ фициента эффективной вязкости v от объемной концентрации р показана на рис. 2 кривой 2.

В качестве простейшей аппроксимации (12) в данной работе также использовалась функция

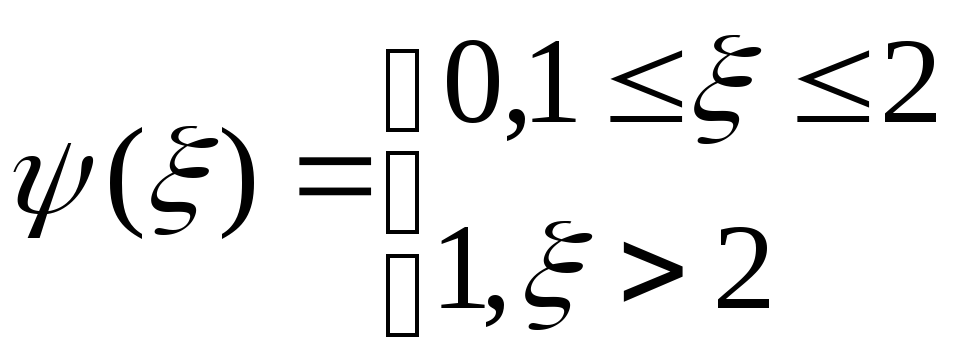
О О,1 0,2 O,3 0,4 р

Рис. 2. Зависимость безразмерной вязкости суспензии от объемной концентрации: 1 — мо­дель взаимопроникающих частиц; 2 — модель, использующая БФР в виде ступеньки; 3 — мо­дель с кольцом, формула (14); 4 — использую­щая БФР [3]; 5 —ячеечная модель J6}; заштри­хованная область — экспериментальные дан­ные [7]

(рис. 1, ломаная линия 5). В этом случае задача (7), (8) имеет аналити­ческое решение, подстановка которого в (10) дает следующее уравнение, определяющее зависимость v от р:

(14)

(рис. 2, кривая 3). Используя БФР [3], из (5) в данной работе численно была получена зависимость ψ (ξ, p) (рис. 1, кривые 3—5). Результат рас­четов зависимости v от р, выполненных при употреблении этой модели, представлен на рис. 2 кривой 4.

Дли сравнения на рис. 2 приведена зависимость v от р, полученная в [6] на основе ячеечной модели.

Сравнение теоретических и опытных данных показывает, что модель проницаемых частиц дает довольно хорошие результаты для умеренно концентрированных суспензий, но завышает значения коэффициента эф­фективной вязкости суспензий «средней» концентрации, а при p→40% значение эффективной вязкости суспензии обращается в бесконечность.

Заштрихованную область на рис. 2 образуют экспериментальные дан­ные шестнадцати работ, обзор которых дан в [7]. Значительный разброс опытных данных связан с влиянием большого количества факторов на ре­зультат проводимых измерений: типа используемого вискозиметра [8], отношения размеров частиц и области течения [8, 9], величины скорости сдвига [10] и т. п.

Учет непроницаемости частиц становится необходимым при опреде­лении реологических характеристик суспензии концентрации более 20—25%.

Перенос тепла. Рассмотрим перепое тепла в дисперсной среде, oбe фазы которой могут быть подвижны, в предположении, что число Пекле характеризующее локальный конвективный перенос вблизи отдельных частиц дисперсной фазы, обтекаемых непрерывной фазой, мало по срав­нению с единицей. Очевидно, что рассматриваемая модель справедлива и для композитных материалов, матрица и дисперсная фаза которых имеют разные коэффициенты теплопроводности.

Согласно [11], в которой можно найти также ссылки на другие рабо­ты, коэффициент эффективной теплопроводности представим в виде

(15)

где неизвестный параметр γ определяется из уравнения (ср. с формулой (2))

(16)

а для определения усредненной по ансамблю соседних частиц температу­ры τ0* (а/0) на поверхности пробной частицы (16) становится следующая краевая задача:

(17)

Функция ψ (ξ, p) определяется видом БФР согласно (5).

При помощи изложенного выше метода разложения решения в ряд по сферическим функциям в данной работе была решена задача (17) и определена зависимость β от ρ и х (рис. 3). При расчетах использовалась БФР, полученная в [3] (см. выше).

Как видно из рис. 3, зависимость теплопроводности дисперсной среды от отношения теплопроводностей дисперсной и непрерывной фаз наибо­лее существенна при . При х<0,1 и х>100 эффективная теплопро­водность практически совпадает с ее значениями в предельных случаях и , т. е. когда дисперсная фаза состоит из абсолютно непроводящих или идеально проводящих частиц соответственно.

Используя тот факт, что перенос тепла, массы или электрических за­рядов при используемых предположениях описывается математически эквивалентными уравнениями и, следовательно, безразмерные эффектив­ные коэффициенты переноса этих субстанций совпадают, результаты проведенных расчетов на рис. 3 сравниваются с опытными данными [12— 15] по электропроводности стабильных эмульсий. Видно, что согласие между экспериментом и теорией достаточно хорошее.

Сравнение с имеющимися в литературе данными об эффективной теп­лопроводности стационарного зернистого слоя в общем случае не пред­ставляется возможным, так как в данной работе не учитывается перенос тепла по дисперсной фазе за счет контактов частиц.

Для сравнения различных моделей на рис. 4 представлено семейство зависимостей β = β (x, р) при х=100 и x=0,1, полученное ранее при ана­логичных (сделанных выше) следующих предположениях [11]: при пре­небрежении неперекрываемостью частиц — кривые 1; при использовании простейшего представления ψ (ξ, p), учитывающего непроницаемость частиц, в виде (13) —2; ψ (ξ) задается в виде (12) —3. Там же на рис. 4 представлены результаты расчетов, выполненные в данной работе,— кривые 4.

Из сравнения рис. 2 и 4 видно, что результаты расчетов, выполненных с использованием различных видов БФР, учитывающей непроницаемость частиц (кривые 2, 3, 4 на рис. 2 и 4), при определении эффективной теп-лопроводностн дают практически одинаковые результаты. Наоборот, зна­- чения коэффициента эффективной вязкости, как следует из рис. 2, в большой степени зависят от вида БФР. В связи с изложенным выше ста­новится понятной причина большого разброса экспериментальных дан­ных по значению коэффициента эффективной вязкости суспензии и зна­чительно меньшего расхождения опытных данных по величине коэффи-

Рис. 3. Зависимость относительной теплопроводности дисперсной среды от объемной концентрации: 1 — при х = 0; 2 — 0,172; 3 — 3; 4—15,7; 5—100; 6— >> 1: эксперимен­тальные данные при х=0: а — [12]; б—[13]; в — [14]; г — [15]; д — при х=0,172; е —

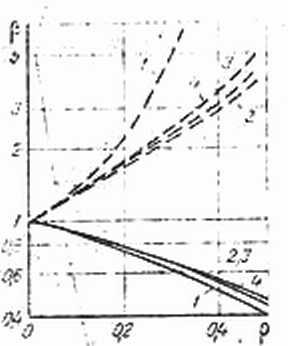
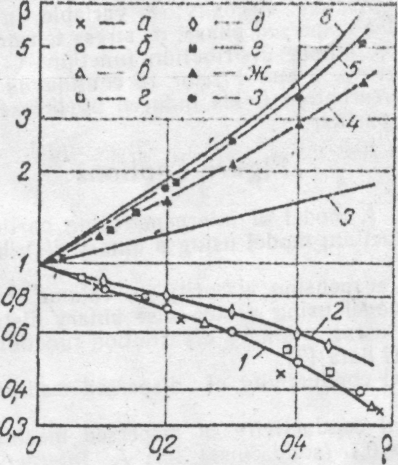
>>1: ж— 15,7; з— 101

Рис. 4. Зависимость относительной теплопроводности дисперсной среды от объемной концентрации при х=100 — штрих и х=0,1—сплошные линии согласно моделям: 1 — взаимопроникающих частиц; 2 — с кольцом; 3— использующей БФР в виде ступеньки

[3]; 4 — результаты данной работы

циента эффективной теплопроводности. Это связано со структурирова­нием дисперсной фазы, наблюдающимся в реальных условиях и приводя­щим к изменению вида БФР.

Обозначения

а — радиус частицы; Ai, Вi,— коэффициенты в (11); с — скорость в лабораторной системе координат r; d — плотность; е — тензор скоростей.деформации; f_m, F_m, g_m, G_m, l_m, L_m—функции в (6); I — единичный тензор; Е — вектор средней плотности тепло­вого потока; K⁽¹⁾ ,K⁽²⁾— коэффициенты в (9); m — порядок сферической гармонии: n — единичный вектор внешней нормали к поверхности пробной частицы; N — число частиц в объеме; р — давление; v—скорость в конвективной системе координат х, свя­занной с центром пробной частицы; х' — радиус-вектор центра частицы; y(z) —функция в (11); z — независимая переменная в (П); β— безразмерный коэффициент эффективной теплопроводности; γ — коэффициент в (15); ε — порозность; η— переменная в (5); х— отношение теплопроводностей дисперсной и непрерывной фаз; λ — коэффициент теплопроводности; μ — коэффициент вязкости; ν — безразмерный коэффициент эффек­тивной вязкости; ξ — переменная в (3) и далее; ρ — объемная концентрация дисперсной фазы; σ — тензор напряжений; τ—температура; Ф — потенциал внешних массовых сил; φ— бинарная функция распределения; ψ — функция, определяемая (4); ω — угловая скорость; нижние индексы нуль и единица относятся соответственно к непрерывной и дисперсной фазам; звездочка означает диадное перемножение; крышечка сверху - поля возмущений, индуцируемых пробной частицей; звездочкой сверху отмечена температура внутри пробной частицы.

Литература

_{1. Буевич Ю. А., Щелчкова И. Н. ИФЖ, 33, 872, 1977.}

_{2. Буевич Ю. А., Марков В. Г., ПММ, 36, 480, 1972.}

_{3. Бородуля В. А., Буевич Ю. А. ИФЖ, 35, 889, 1978.}

1