СХОДИМОСТЬ РЯДОВ ТЕОРИИ ВОЗМУЩЕНИЙ В ЗАДАЧЕ О РАСПРО- СТРАНЕНИИ КОРОТКИХ ВОЛН В СЛУЧАЙНО НЕОДНОРОДНОЙ СРЕДЕ.

Рассматривается решение параболического уравнения Леонтовича, описывающего распространение коротких волн в случайно неоднородной среде. Предполагается, что проницаемость среды флуктуирует по гауссову закону и начальное условие задается в виде волнового пакета с квадратично интегрируемой амплитудой. Показывается, что ряды теории возмущений для среднего по ансамблю поля и функции взаимной когерентности поля, удовлетворяющего параболическому уравнению, сходятся по нормам соответствующих гильбертовых пространств при весьма слабом ограничении на вид корреляционной функции флуктуаций проницаемости и произвольном значении пройденной волной дистанции. Получены строгие оценки погрешностей вычисления сумм этих рядов с помощью уравнений Дайсона в приближении Бурре, составленных исходя из параболического уравнения.

В последнее время в ряде работ распространение волн в случайно неоднородной среде с крупномасштабными неоднородностями описывается параболическим уравнением Леонтовича. Поэтому представляет интерес найти решение этого уравнения при наиболее общих предположениях о статистических свойствах среды.

В работе Татарского параболическое уравнение решается в марковском приближении, когда флуктуации проницаемости среды распределены по гауссову закону и дельта - коррелированы в направлении падения волны.

В данной работе исследуется решение параболического уравнения, описывающего распространение волн в случайно неоднородной среде с гауссовыми флуктуациями проницаемости, без использования предположения о том, что эти флуктуации дельта - коррелированы в направлении падения волны.

1.Стохастические уравнения.

Параболическое уравнение Леонтовича удобно записать в виде уравнения Шредингера

(1) где u(p, t) - комплексная амплитуда поля, V(p,t)=-k₀² (x, р) - эффективный потенциал среды, ε(x, p) - флуктуирующая часть ее проницаемости, k₀ - волновое число в свободном пространстве (в отсутствие флуктуаций проницаемости), t=x/2k₀, х - продольная и р - поперечные координаты по отношению к первоначальному направлению распространения волны, Δ - оператор Лапласа по поперечным координатам p. К уравнению (1) добавляется начальное условие.

(2)

Предполагаем, что проницаемость ε^~(х, р) есть гауссова случайная функция от х, р.

Обозначим через K(p, p’, t) функцию Грина свободного пространства, удовлетворяющую уравнению (1) при V(p, t)0 и начальному условию

.

Уравнение (1) с начальным условием (2) сводится к интегральному

с неоднородным членом

. В операторной форме

(3) где через u₀(0) обозначено u₀(р).

Наряду с полем u(р, t) рассматриваем его билинейную комбинацию

где звездочка указывает на переход к комплексно-сопряженной величине. Интегральное уравнение для γ(p1, p2, t) при начальном условии

γ(p1, p2, 0) = γ(p1, p2) (4) в операторной форме аналогично уравнению (3) и записывается как

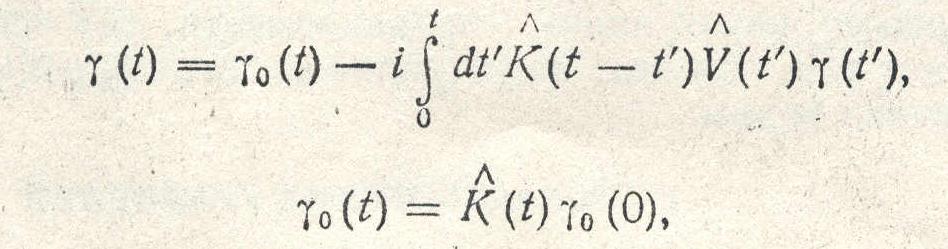(5)

где через К(t) обозначена тензорная функция Грина свободного пространства с ядром

переводящая при своем действии функции от p₁’ p₂’ в функции от p_1, р₂; через V(p₁, p₂, t), обозначен тензорный потенциал

и через γ₀(0) обозначено γ₀ (p₁, р₂).

2.Ограничения на начальные условия.

Будем считать, что начальные условия (2) и (4) для поля и его билинейной комбинации задаются в виде волновых пакетов с квадратично интегрируемыми функциями u₀(p) γ₀(p₁, p₂).На этих функциях определяются гильбертовы пространства H₁ и H₂ со скалярными произведениями:

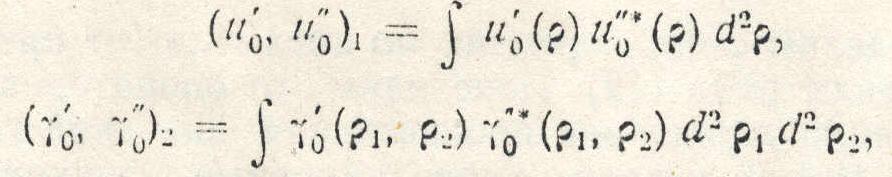(6) где штрихами отмечаются различные начальные условия. Скалярным произведениям(6) отвечают нормы || u₀ || ₁ и || γ₀ || ₂ в H₁ и H₂.

Функция Грина K(t), как хорошо известно из квантовой механики, представляет собой унитарный оператор в Н₁, т. е. при своем действии сохраняет скалярное произведение функций и имеет единичную норму.Из унитарности функции Грина К(t) в Н₁ следует унитарность тензорной функции Грина К^(t) в Н₂. Таким образом,

(7) Операторы умножения E (χ) и E^(χ₁,χ₂)на осциллирующие экспоненты, действующие в Н₁ и Н₂ согласно

₍₈₎ где χ, χ₁, χ₂ - вещественные векторы, также унитарны:

(9)

Нам встретятся операторные интегралы вида

(10) где А = А(ω) - операторная функция параметра ω, каждое значение которой А есть оператор, действующий в Н₁ или Н₂ ,f(ω) – комплексная функция. Норма оператора I, действующего в H₁ или Н₂, оценивается интегралом

(11)

3. Ряды теории возмущений для среднего поля и функции взаимной когерентности.

Представим решения интегральных уравнений (3) и (5) для u(t) и γ(t) в виде рядов теории возмущений и усредним их по ансамблю флуктуаций проницаемости. В результате получаем ряды для среднего поля u(t) =< и(t) > и функции взаимной когерентности γ(t)=<γ(t)>, где угловые скобки означают усреднение по ансамблю.

Так как операторные формы уравнений (3) и (5) для поля и его билинейной комбинации аналогичны, ограничимся описанием исследования ряда теории возмущений для среднего поля u(t). Этот ряд имеет вид

(12)

Определим смысл средних по ансамблю от произведений операторов в членах ряда (12).Переходим от операторов к ядрам и используем правило усреднения произведения значении гауссовой случайной функции. Раскладываем корреляционные функциипотенциала V(p, t) в интегралы Фурье по поперечным координатам р и р', обозначая их фурье - образы через В (χ, t;χ',t ). Вводим операторы умножения Е(χ), действующие согласно первому равенству (8). Возвращаемся от ядер к операторам. Эти преобразования приводят к равенствам

(13) где сумма справа берется по всем разбиениям α чисел 1,2, ... , 2n на n групп α ₁, α ₂, … , α _2n-1, α _2n по два числа в каждой группе.

Правые части равенств (13) имеют вид операторных интегралов (10). Оценивая их нормы с помощью первых равенств (7), (9) и неравенства (11), находим, что ряд (12) мажорируется по норме H₁следующим рядом:

(14) где через B(t, t') обозначена положительная функция, для которой интеграл

(15)

Чтобы свернуть мажорантный ряд (14) в конечное выражение, рассмотрим вспомогательный одномерный случайный процесс ξ(t), удовлетворяющий уравнению

(16) где v(t) —гауссова случайная функцией функция с корреляционной

Вычисляя среднее по ансамблю k(t) = <ξ(t) от решения уравнения (16) с помощью характеристического функционала для v(t) и с помощью ряда теории возмущений, приходим к выводу, что сумма мажорантного ряда (14) равна k(t) || u ₀(0) ||, где функция k(t) равна

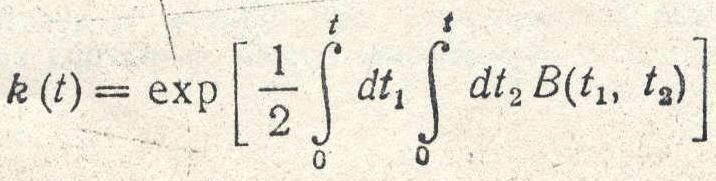
Окончательно оказывается, что сумма u(t) ряда (12) подчиняется оценке

(17)

При исследовании сходимости ряда теории возмущений для функции взаимной когерентности γ(t) появляются фурье - образы корреляционных функций тензорного потенциала V^(p₁, p₂, t) по поперечным координатам p₁,p₂. Каждый такой фурье - образ равен сумме четырех слагаемых, содержащих в качестве множителей дельта - функции* от χ -аргументов. Поэтому сначала раскладываем в членах ряда теории возмущений произведения фурье - образов корреляционных функций тензорного потенциала по формуле бинома Ньютона и интегрируем по χ - аргументам всех дельта - функций, а уже потом используем неравенство (11). В остальном исследование сходимости ряда для γ(t) аналогично исследованию ряда для u(t), и его сумма подчиняется оценке

(18) где функция

Оценки (17) и (18) показывают, что ряды теории возмущений для среднего поля и функции взаимной когерентности поля, удовлетворяющего параболическому уравнению (1), сходятся по нормам Н₁ и Н₂ при условии ограниченности интеграла в левой части неравенства (15) и любом значении пройденной волной дистанции.