Московский Институт Электронной Техники (Технический Университет)

Курсовая работа.

Квантовая механика и статистическая физика.

Тема: Многоатомные молекулы.

Выполнил: студент группы

ЭКТ-21 Вавер. Н. А.

Проверила: Туманова. Л.А.

Москва 2002 г.

Содержание:

1. Классификация молекулярных колебаний.

2. Колебательные уровни энергии.

3. Устойчивость симметричных конфигураций молекул.

4. Квантование вращения волчка

5. Взаимодействие колебаний и вращения молекулы.

6. Классификация молекулярных термов.

Многоатомные молекулы.

Классификация молекулярных колебаний.

В применении к многоатомным молекулам теория групп прежде всего решает вопрос о классификации их электронных термов, т.е. уровней энергии при заданном расположении ядер. Они классифицируются по неприводимым представлениям точечной группы симметрии, которой обладает рассматриваемая конфигурация ядер. Обычно речь идет о расположении, соответствующему положению равновесия ядер. В этом случае классификация продолжает иметь известный смысл и при малых колебаниях ядер, но, конечно, теряет смысл, если колебания нельзя рассматривать как малые.

В двухатомной молекуле мы не сталкивались с таким вопросом, так как ее аксиальная симметрия сохраняется, разумеется, при любом перемещении ядер. Аналогичное положение имеет место и для трехатомных молекул.

Для нормальных электронных термов многоатомных молекул имеет место эмпирическое правило, согласно которому у подавляющего большинства молекул волновая функция нормального электронного состояния обладает полной симметрией.

Применение методов теории групп особенно существенно при исследовании молекулярных колебаний.

Как известно из механики, система из Nчастиц обладает 3N-6 колебательными степенями свободы; из общего числа 3Nстепеней свободы три соответствуют поступательному и три – вращательному движению системы как целого. Энергия системы частиц, совершающих малые колебания,

E=0.5 ∑ m_ik Ú_i Ú_k + 0.5∑k_iku_iu_k (100.1)

^{i, k i, k}

где m_ik,k_ik – постоянные коэффициенты, аu_i – компоненты векторов смещения частиц от их положения равновесия. Соответствующим линейным преобразованием величинu_i , можно колебательные координаты выбрать таким образом, чтобы обе квадратичные формы в (1) превратились в суммы квадратов. Нормируя эти координаты так, чтобы обратить все коэффициенты в выражении кинетической энергии в единицу, получим колебательную энергию в виде

E=0.5∑ Q^{’ 2} _{α i} + 0.5∑ω²_α∑Q²_{α i} (100.2)

^{i, α α i}

Колебательные координаты Q_αiназываютсянормальными;ω_α - частоты соответствующих им независимых колебаний. Может оказаться, что несколько нормальным координат соответствует одна и та же частота; индексα у нормальной координаты соответствует номеру частоты, а индексi=1, 2, … , f_α нумерует координаты, относящиеся к одной и той же частоте. Сумма квадратов∑Q²_αi остается изменой. Кратность частоты определяет размерность представления. ⁱ

Совпадение частот, соответствующих двум различным неприводимым представлениям, было бы невероятной случайностью. Поскольку физически нормальные координаты являются по самому своему существу вещественными величинами, то два комплексно сопряженных представления соответствуют одной собственной частоте вдвое большей кратности.

Эти соображения дают возможность произвести классификация собственных колебаний молекулы без того, чтобы решать сложную задачу о конкретном определении ее нормальных координат.

Для нахождения полного колебательного представления исходим из того, что характеры представления инвариантны относительно линейного преобразования функции базиса. Поэтому для их вычисления можно воспользоваться в качестве функции базиса не нормальными координатами, а просто компонентами u_iвекторов смещения ядер от их положения равновесия.

Прежде всего очевидно, что при вычислении характера некоторого элемента Gточечной группы надо рассматривать только те ядра, которые остаются на месте при данном преобразовании симметрии. Действительно, если при рассматриваемом повороте или отраженииG ядро 1 перемещается в новое положение, где до этого находилось другое такое же ядро 2, то это значит, что при операцииG смещение ядра 1 преобразуются через смещение ядра 2. Другими словами, в соответствующих этому ядру строка матрицыG _{i k} во всяком случае не будет диагональных элементов. Компоненты же вектора смещения ядра, положение равновесия которого не затрагивается операциейG, преобразуются только друг через друга, так что их можно рассматривать независимо от векторов смещения остальных ядер.

Рассмотрим сначала поворот C(φ)на уголφвокруг некоторой оси симметрии. Пустьu _x , u _y , u _z– компоненты вектора смещения некоторого ядра, положение равновесия которого находиться на самой оси и потому не затрагивается поворотом. При повороте эти компоненты преобразуются, как и компоненты всякого обычного (полярного) вектора, по формуле

u^’_x = u_x cos φ + u_y sin φ,

u^’_y= -u_x sin φ + u_y cos φ,

u^’_z= u_z

Характер т.е. сумма диагональных членов матрицы преобразования, равен 1+ 2 cos φ. Если всего на данной оси расположеноN_cядер, то суммарный характер равен

N_c(1 + 2 cos φ). (100.3)

Однако этот характер отвечает преобразованию всех 3NсмещенииU_i. Поступательное перемещение определяется вектором смещенияUцентра инерции молекулы; соответствующая часть характера, следовательно, равна1 + 2 cos φ. Поворот же молекулы как целого определяется векторомδΩугла поворота. ВекторδΩесть аксиальных вектор; но по отношению к поворотам системы координат аксиальный вектор ведет себя так же, как и полярный вектор. Поэтому векторуδΩтоже соответствует характер, равный1+2cos φ. Всего, следовательно, мы должны вычислить из(100.3)величину2(1+2cos φ). Таким образом окончательно находим характерχ(C)поворотаС(φ)в полном колебательном представлении:

Χ(С) = (N_c -2) (1 + cos φ) (100.4)

Характер единичного элемента Eравен, очевидно, просто полному числу колебательных степеней свободы:χ(E) = 3N – 6.

Аналогичным образом вычисляем характер зеркально – поворотного преобразования S (φ)(поворот на уголφвокруг осиZи отражение в плоскостиXY). При этом преобразовании вектор преобразуется согласно формулам:

u^’_x = u_x cos φ + u_y sin φ,

u^’_y= - u_x sin φ + u_y cos φ,

u^’_z= -u_z

чему соответствует характер равный (-1+2cosφ). Поэтому характер представления, осуществляемого всеми3NсмещениямиU_i . равен

N_s (-1 + cosφ) (100.5)

Где N_s – число ядер, не затрагиваемых операциейS(φ)(это число может быть либо нулевым, либо единицей). ВекторуLсмещения центра инерции соответствует характер(-1+2 cosφ). Что же касается вектораδΩ, то, будучи аксиальным вектором, он не меняется при инверсии системы координат; с другой стороны, зеркально – поворотное преобразованиеS(φ)можно представить в виде

S(φ) = C(φ) σ_h = C(φ) C₂I = C(π + φ)I

т.е. как поворот на угол π+φвместе с последующей инверсией. Поэтому характер преобразованияS(φ), примененного к векторуδΩ, равен характеру преобразованияC(π + φ), примененному к обычному вектору, т.е. равен1+2cos(π+φ) = 1-2cosφ. Сумма(-1 + cosφ) +( 1-2cosφ) =0, так что мы приходим к результату, что выражение(100.5)непосредственно равно искомому характеруχ(S)зеркально-поворотного преобразованияS(φ)в полном колебательном представлении:

χ(S)= N_s (-1 + 2cosφ).(100.6)

В частности, характер отражения в плоскости (φ=0)равенχ(σ)=N_σ, а характер инверсии(φ= π)равенχ(I) =-3N_I .

Число степеней свободы при движении N частиц вдоль прямой равноN; из них одна соответствует поступательному перемещению молекулы как целого. Поэтому число нормальных координат колебаний, оставляющих атомы на прямой, равноN – 1; им соответствуют, вообще говоря,N – 1различных собственных частиц. Остальные(3N-5) – (N – 1) =2N – 4нормальных координат относятся к колебаниям, нарушающим прямолинейность молекулы; им соответствуютN – 2различные двукратные частоты.

Колебательные уровни энергии.

При квантовомеханическом рассмотрении колебательная энергия молекулы определяется собственными значениями гамильтониана

Ĥ^(v) = 0.5 , (101.1)

где ∂∕∂Q_αί – операторы импульсов, соответствующих нормальным координатамQ_αί . Поскольку этот гамильтонианиан распадается на сумму независимых слагаемых, то уровни энергии представляются суммами

E^(v)= , (101.2)

где , а - кратность частоты . Волновые же функции представляются произведениями соответствующих волновых функций линейных гармонических осцилляторов

, (101.3)

где

; (101.4)

обозначает полином Эрмита-й степени, а .

Если среди частот имеются кратные, то колебательные уровни энергии, вообще говоря, вырождены. Энергия(102,2)зависит только от суммы. Поэтому кратность вырождения равна числу свобод, которыми можно составить данный набор чиселиз числа.

Полная кратность вырождения равна

. (101.5)

Для двукратных частот множители этого произведения равны +1, а для трехкратных0.5(+1)(+2).

Функции, относящиеся к разным частотам, преобразуются независимо друг от друга. Экспоненциальный множитель в (101.4)инвариантен по отношению ко всем преобразованиям симметрии. В полиномах Эрмита члены каждой данной степени преобразуются только друг через друга. Поскольку, с другой стороны, каждый полином Эрмита вполне определяется своим высшим членом, то, написав+ члены низших степеней, достаточно рассматривать только высший член.

Рассмотрим подробнее двухмерные представления. Пусть χ(G)есть характер некоторого элемента группы в данном двухмерном представлении, причем χ(G). Сумма диагональных элементов матрицы преобразования компонентx, yдвухмерного вектора при повороте в плоскости на уголφравна2cos φ. Приравняв2cos φ= χ(G), мы найдем угол поворота, формально соответствующего элементуGв данном неприводимом представлении.

(101.7)

Случай χ(G)=0требует особого рассмотрения так как равный нулю характер отвечает как поворот на уголπ ∕2, так и отражению. Если , то мы имеем дело с поворотом на уголπ ∕2и дляполучим

.(101.8)

Если же χ(G)=2, тоχ(G)надо рассматривать как характер отражения ( т.е. преобразования ,); тогда

. (101.9)

Устойчивость симметричных конфигураций молекул.

Пусть - гамильтониан электронного состояния молекулы, в котором расстояния между ядрами рассматриваются как параметры. Посредствомобозначим этот гамильтониан при заданной симметричной конфигурации. В качестве величин, определяющих малые смещения ядер, можно воспользоваться нормальными колебаниями координатQ_αί. Разложение по степеням Q_αίимеет вид

(102.1)

Коэффициенты V, W,…разложения – функции только от координаты электронов. При преобразовании симметрии величины Q_αίпреобразуются друг в друга.

Рассмотрим некоторый вырожденный электронный терм E₀. Смещение ядер, нарушающее симметрию молекулы, приведет, вообще говоря, к расщеплению терма. Величина расщепления определится, с точностью до членов первого порядка относительно смещений ядер, секулярным уравнением, составленным из матричных элементов от линейного члена разложения(102.1)

V_ρσ =∑Q_αί ∫ψ_ρV_αί ψ_σdq (102.2)

^{α, ί}

где ψ_ρ, ψ_σ – волновые функции электронных состояний, относящихся к данному вырожденному терму. Устойчивость симметричной конфигурации требует, чтобы линейное поQрасщепление отсутствовало, т.е. все корни секулярного уравнения должны тождественно обратиться в нуль. При этом, разумеется, мы должны рассматривать только те из нормальных колебаний, которые нарушают симметрию молекулы, т.е. должны отбросить полно-симметричные колебания.

Поскольку Q_αί произвольны, то матричные элементы(102.2)исчезают только, если все интегралы

∫ ψ_ρV_αίψ_σ dq.(102.3)

Пусть D^(el)– неприводимое представление, по которому преобразуются электронные волновые функцииψ_ρ, аD_α– то же для величинV_αί. Согласно интегралы(102.3)будут отличны от нуля, если произведение[D^{(el) 2}]D_αсодержит в себе единичное представление, или, что тоже, если[D^{(el) 2}]содержит в себе в себеD_α . В противном случае все интегралы обратяться в нуль.

Рассмотрим, например, молекулы типа CH₄, в которой один атом(С)находится в центре, а четыре(Н)– в вершинах тетраэдра. Такая конфигурация имеет симметриюT_d. Вырожденные электронные термы соответствуют представлениямE, F₁, F₂этой группы. Молекула обладает одним нормальным колебаниемА₁(полно-симметричное колебание), одним двукратнымЕи двумя трехкратнымиF₂. Симметричные произведения представленийE, F₁, F₂самих на себя равны

[E²] = A₁ + E, [F₁²] = [F₂²] = A₁ + E + F₂.

Мы видим, что каждое из них содержит по крайней мере одно из представлений Е, F₂, и потому рассматриваемая тетраэдрическая конфигурация при вырожденных электронных состояниях оказывается неустойчивой.

Этот результат является общим правилом, составляющий содержание так называемой теоремой Яна – Теллера: при вырожденном электронном состоянии всякое симметричное расположение ядер( за исключением расположенных на одной прямой) неустойчиво. В результате этой неустойчивости ядра сместятся так, чтобы симметрия их конфигурации нарушилась настолько, что вырождение терма окажется полностью снятым. В частности, можно утверждать, что нормальным электронным термом симметричной (нелинейной) молекулы может быть только невырожденный терм.

Исключение, как уже упомянуто, представляют только линейные молекулы. Конструктивное общее доказательство теоремы основано на следующем замечании.

Вырождение электронных состояний связано с симметрией расположения ядер, может существовать только в таких точечных группах симметрии молекулы, которые содержат по крайней мере одну поворотную (С_n) или зеркально – поворотную(S_n)ось порядкаn>2. в таком случае среди волновых функций взаимно вырожденных состояний имеется по крайней мере одна, для которой электронная плотность не инвариантна по отношению к поворотам вокруг этой оси; вместе с электронной плотностью не будет симметрично по отношению к оси также и создаваемое электронами электрическое поле. В тоже время в молекуле существует расположенные не на оси эквивалентные ядра – ядра, переводящиеся друг в друга поворотамиC_n (илиS_n). Таким образом, эквивалентные ядра оказываются лежащими в неэквивалентных точках электрического поля. Но не требуемая симметрией поля эквивалентность положений равновесия заряженных частиц в нем невозможна в том смысле, что она могла бы быть связана лишь с невероятной случайностью.

Рассмотрим какое-либо ядро, лежащее вне «центра» молекулы и не на главной оси симметрии, если таковая имеется. Пусть Hесть совокупность тех преобразований симметрии молекулы, которые оставляются ядроа неподвижным;Нявляется одной из подгрупп полной группы симметрии молекулыGи может представлять собой одну из точечных группС_1, С_s, C_n ,C_nv. Преобразования изG, не входящие вН, переводят ядроав другие, эквивалентные ему ядра,… ; пустьs– число ядер в этой совокупности. Очевидно, что порядок подгруппыHравенg/s, гдеg– порядок всей группыG.

Число sзаведомо , так как для предполагаемого существования неодномерного неприводимого представлениянеобходимо наличие по крайней мере одной оси симметрии порядка более высокого, чем2, причем ядроaпо условию на ней не находится.

Представление D^(el)группыGпо отношению к группеHболее низкой симметрии, вообще говоря, приводимо. Предположим, что в его разложении по неприводимым представлениям группыHимеет одномерное; назовем егоd^(el). Оно осуществляет электронной волновой функциейψ – одной из функций базиса представленияD^(el). Поскольку представленийd^(el) одномерно, квадратρ=ψ² инвариантен по отношению ко всем преобразованиям изH, т.е. осуществляет единичное неприводимое представление этой группы.

Такое же представление группы Hможно осуществить, взяв в качестве базиса одно из смещенийQ_aатомаа- смещение в направлении вдоль радиуса – вектора, проведенного к ядруа из центра молекулы.

Применив теперь к этому смещению все операции группы G , мы получим базис некоторого представления этой группы; назовем егоD_Q. Поскольку всякое преобразование изG, не входящее вH, переводит смещениеQ_aсмещение одного из другихs- 1 эквивалентных ядер,… , а смещения различных яде, разумеется, линейно независимы, то размерностьD_Qравнаs. При этом смещения,,…, образующие базисD_Q, заведомо не могут отвечать ни чистому переносу, ни чистому повороту молекулы как целого: при наличии трех или более эквивалентных ядер из их радиальных смещений нельзя составить таких перемещений.

Таким же путем можно получить представление группы G, применив все ее преобразования к функции = ²; назовем это представлениеD_.РазмерностьD_ может быть равнойs, но может оказать и меньше, так как нет заведомых оснований полагать, что всеsфункции, G’, G”, ...линейно независимы. Можно, однако, утверждать, что представлениеD_, если и не будет совпадать сD_Q, то во всяком случае будет целиком содержаться в нем. Кроме того, оно не является единичным, так как квадрат²заведомо не инвариантен по отношению ко всей группеG(инвариантна лишь сумма квадратов всех функций базиса неодномерного не приводимого представленияD^(el)).

Установленные таким образом свойства представлений D_QиD_сразу дают требуемый результат. Действительно,D_Q– часть полного колебательного представления, аD_- часть представлений[D^(el)2]. Тот факт, чтоD_содержится вD_Q, означает, следовательно, что[D^(el)2]содержит в себе, по крайней мере, одно из неединичных колебательных представленийD_, что и требовалось доказать.

В изложенных рассуждениях, однако, еще предполагалось, что в разложении представлений D^(el)по неприводимым представлениям подгруппHимеется одномерное. Это предположение выполняется в подавляющем большинстве случаев. Так, оно заведомо справедливо, еслиH =C₁, C_s, C₂, C_2v(поскольку все неприводимые представления этих групп одномерны). Оно заведомо справедливо и приH=C_n, C_nvсn>2, если размерностьD^(el)нечетна (поскольку группыC_n, C_nv имеют лишь одно и двумерные неприводимые представления). Рассмотрение таблиц характеров неприводимых представлений точечных групп показывает, что исключением являются двумерные представления кубических группG=O, T_d, O_hпо отношению к подгруппамH=C₃,C_3v.

Будем говорить для определенности о группе G=O и подгруппеH=C₃(что отражается только на обозначениях представлений). Две электронные функции₁, ₂осуществляют представлениеD(el)=EгруппыO, и они же – представлениеd ^(el) = EподгруппыC₃. Представление же группыС₃, осуществляемое произведениями₁², ₂², ₁₂, есть[E²] = A + E. Такое же представление подгруппыC₃осуществляется тремя компонентами векторов произвольного смещенияQ_aядраaв качестве базиса. ПредставлениеD_группыО есть в данном случаеD_ = [D^(el)2] =A₁ + E; оно не содержит в себе представленийF₂, отвечающего вектору переноса или поворота молекулы как целого, и содержит (наряду с единичным) также и неединичное представление. Поэтому тот факт, чтоD_содержится в представленииD_Q(в данном случае3s-мерном), доказывает неустойчивость молекулы и в этом случае.

В соответствии с оговоркой в начале этого параграфа во всем предыдущем изложении вырождение электронных состояний подразумевалось имеющим чисто орбитальное происхождение. Укажем, однако, что теорема Яна-Теллера остается справедливой и при учете спин-орбитальных и спин-спиновых взаимодействий, с тем лишь отличием, что в молекулах (нелинейных) с полуцелым спином не приводит к неустойчивости двукратное крамеровское вырождение. Последнему случаю отвечают двумерные двузначные неприводимые представления двойных точечных групп. В отсутствии неустойчивости в этом случае можно убедиться уже следующим формальным образом. Для выяснения правил отбора матричных элементов в случае двузначных представлений D(el)надо рассматривать не симметричные, а антисимметричные произведения{D ^{(el) 2}}. Но для всех двузначных неприводимых представлений с размерностью2эти произведения совпадают с единичным представлением, т.е. заведомо не содержат в себе представлений, отвечающих каким-либо не полно-симметричным колебаниям молекулы.

Квантование вращения волчка

Исследование вращательных уровней многоатомной молекулы часто затрудняется необходимостью рассматривать вращение одновременно с колебаниями. В качестве предварительной задачи мы рассмотрим вращение молекулы как твердого тела, т.е. с “жестко закрепленными атомами” (волчок).

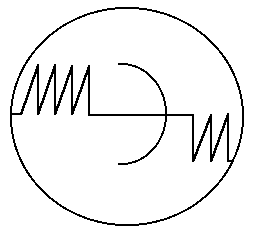
П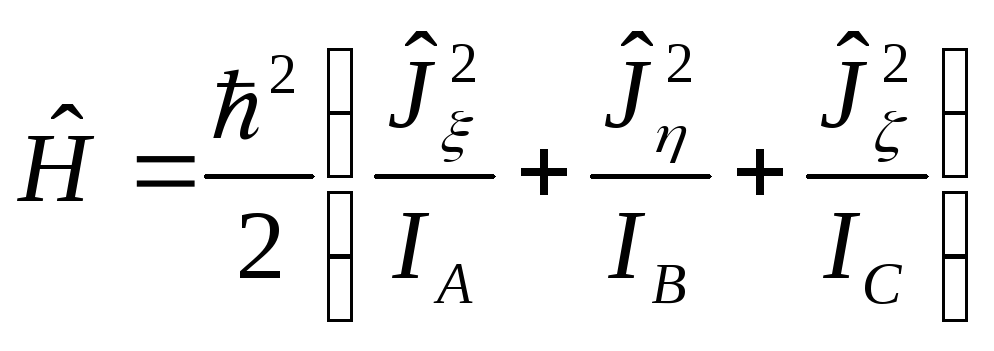усть - система координат с осями, направленными вдоль трех осей инерции волчка и вращающаяся вместе с ним. Соответствующий гамильтониан получается заменой компонентJ_, J_,J_ его момента вращения в классическом выражении для энергии соответствующими операторами:

где I_A, I_B, I_c - главные моменты инерции волчка.

Правила коммутации для операторов J_, J_, J_компонент момента во вращающейся системе координат не очевидны, так как обычный вывод правила коммутации относится к компонентамJ_x, J_y, J_z в неподвижной системе координат. Их, однако, легко получить, воспользовавшись формулой

где a, b– два произвольных вектора, характеризующих данное тело (и коммутативных друг с другом). Эту формулу легко проверить, производя вычисление левой стороны равенства в неподвижной системе координатxyzс помощью общих правил коммутации компонент момента, друг с другом и с компонентами произвольного вектора.

Пустьaиb– единичные векторы вдоль осейи. Тогда[ab]– единичный вектор вдоль оси, и

Аналогично получаются ещё два соотношения. Таким образом, правила коммутации операторов компонент момента во вращающейся системе координат отличаются от правил коммутации в неподвижной системе лишь знаком в правой стороне равенства. Отсюда следует, что и все, полученные ранее из правил коммутации результаты для собственных значений и матричных элементов имеют место и для J_, J_, J_ с той лишь разницей, что все выражения надо заменить комплексно им сопряженными. В частности все значенияJ_пробегают значения

k= - J, ... ,+J, гдеJ(целое число!) – величина момента волчка.

Шаровой волчок.

Нахождение собственных значений энергии вращающегося волчка наиболее просто для случая, когда все его три главных момента инерции одинаковы: 1_А = 1_В = 1_С = I. Для молекулы это имеет место в тех случаях, когда она обладает симметрией одной из кубических точечных групп. Гамильтониан принимает вид:

и его собственные значения равны

(103.4)

Каждый из этих уровней энергии вырожден по 2J + 1 направ­лениям момента относительно самого волчка (т. е. по значениям J_ = k).

Симметричный волчок

Не представляет труда также и вычисление уровней энергии в случае, когда лишь два из моментов инерции волчка совпадают: I_A = I_B  I_C. Это имеет место для молекул, обладающих одной осью симметрии более чем второго порядка. Гамильтониан приобретает вид

(103.5)

Отсюда видно, что в состоянии с определенными значениями J и k энергия равна

(103.6)

чем и определяются уровни энергии симметричного волчка.

Вырождение по значениям k имевшее место для шарового волчка, здесь оказывается частично снятым. Значения энергии совпадают лишь для значений k, отличающихся только знаком, что соответствует взаимно противоположным направлениям мо­мента относительно оси волчка. Поэтому уровни энергии сим­метричного волчка при k0 двукратно вырождены.

Стационарные состояния симметричного волчка характери­зуются, таким образом, тремя квантовыми числами: моментом J и его проекциями на ось волчка (/_s = k) и на фиксированную в пространстве ось г (J_z = М); от последнего числа энергия волчка не зависит. Отметим в этой связи, что сам факт одновременной измеримости величины момента и его проекций на фикси­рованную в пространстве и на жестко связанную с физической си­стемой оси следует из того, что операторы J² и J_z коммутативны

не только друг с другом, но и с оператором J_ =Jn (n — еди­ничный вектор вдоль оси ). Это обстоятельство легко проверить непосредственным вычислением, но оно очевидно и заранее. Оператор момента сводится к оператору бесконечно малого по­ворота, а скалярное произведение Jn двух связанных с волчком векторов инвариантно по отношению к любому повороту системы координат.

Задача об определении волновых функций стационарных со­стояний симметричного волчка сводится, следовательно, к на­хождению общих собственных функций операторов J², J_z, J_. В свою очередь этот вопрос математически тесно связан с зако­ном преобразования собственных функций момента при конечных вращениях. Изменив обозначение квантовых чисел, напишем этот закон в виде

(103.7)

Будем понимать под _JM волновую функцию состояния волчка, описываемого по отношению к неподвижным координатным осям хуг, а под _Jk — волновые функции состояний, описываемых по отношению к связанным с волчком осям . Но в координатах, жестко связанных с физической системой (волчком), величины _Jk имеют определенные значения, не зависящие от ориентации си­стемы в пространстве; обозначим их как ⁽⁰⁾_Jk. Формула же будет давать угловую зависимость функций _JM. Пусть теперь состояние | JM обладает также и определенным значением k проекции момента на ось . Это значит, что из всех величин ⁽⁰⁾_Jk будет отлична от нуля лишь одна — с заданным значением k. Тогда сумма _JM сведется к одному члену:

Тем самым найдена зависимость волновых функций состояний | JMk от углов Эйлера, определяющих поворот осей волчка по отношению к неподвижным осям. Нормируя волновую функцию условием будем иметь

(103.8)

фазовый множитель выбран так, чтобы при k=0 функция переходила в собственную функцию свободного (никак не связан­ного с осью ) целочисленного момента Jс

фазовый множитель выбран так, чтобы при k=0 функция переходила в собственную функцию свободного (никак не связан­ного с осью ) целочисленного момента J с проекцией М, т. е. в обычную (сферическую) функцию.

Асимметричный волчок.

При I_А  I_D  I_C вычисление уровней энергии в общем виде невозможно. Вырождение по направлениям момента относительно волчка здесь снимается полностью, так что данному J соответ­ствует 2J + 1 различных невырожденных уровней. Для вычисле­ния этих уровней (при заданном J) следует исходить из уравнения Шредингера, записанного в матричном виде. Это делается следующим образом.

Волновые функции _Jk состояний волчка с определенными значениями J и - проекции момента — это найденные выше функ­ции (103,8); в этих состояниях энергия асимметричного волчка не имеет определенных значений. Напротив, в стационарных состояниях не имеет определенных значений проекция J_, т. е. уровням энергии нельзя приписать определенных значений k. Волновые функции этих состояний ищем в виде линейных комбинаций

(103.9)

(подразумевается, что все функции — с каким-либо одинаковым для всех значением М). Подстановка в уравнение Шредингера H_J = E_J_J приводит к системе уравнений

(103.10)

а условие разрешимости этой системы дает секулярное уравнение

(103.11)

Корни этого уравнения определяют уровни энергии волчка, после чего система уравнений (103.10) позволит найти линейные комбинации (103.9), диагонализующие гамильтониан, т. е. вол­новые функции стационарных состояний волчка с заданным зна­чением J (и М). Вычисление же матричных элементов какой-либо физической величины по этим волновым функциям сводится, таким образом, к матричным элементам симметричного волчка.

Операторы J_, J_ имеют матричные элементы только для пере­ходов с изменением k на единицу, а J_— только диагональные элементы, в которых надо писать J, k вместо L М). Поэтому операторы J_², J_², J_², а с ними и Н имеют матрич­ные элементы лишь для переходов с k k, k ± 2. Отсутствие матричных элементов для переходов между состояниями с чет­ными и нечетными k приводит к тому, что секулярное уравнение степени 2J + 1 сразу распадается на два независимых уравнения степеней J и J + 1. Одно из них составляется из матричных эле­ментов для переходов между состояниями с четными, а другое — с нечетными значениями k.

Каждое из этих уравнений в свою очередь может быть при­ведено к двум уравнениям более низкой степени. Для этого надо пользоваться матричными элементами, определенными не с по­мощью функций _Jk, а с помощью функций

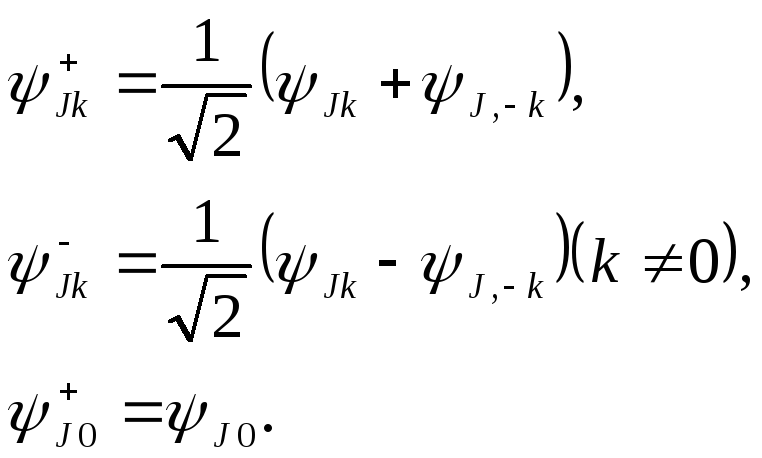
Функции, отличающиеся индексом + и —, обладают различной симметрией (по отношению к меняющему знак k отражению в плоскости, проходящей через ось ), а потому матричные эле­менты для переходов между ними исчезают. Следовательно, можно составлять секулярное уравнения в отдельности для состояний + и состояний —.

Гамильтониан (103.1) обладает специфической симметрией — он инвариантен по отно­шению к одновременному изменению знака любых двух из опе­раторов J_, J_, J_. Такая симметрия формально соответствует группе D₂. Поэтому уровни асимметричного волчка можно клас­сифицировать по неприводимым представлениям этой группы. Таким образом, имеется четыре типа невырожденных уровней, соответствующих представлениям А, В_1,В₂, В₃ .

Легко установить, какие именно состояния асимметричного волчка относятся к каждому из этих типов. Для этого надо выяс­нить свойства симметрии функций _Jk и составленных из нихфункций (103.12). Это можно было бы сделать непосредственно на основании выражений (103.8). Проще, однако, исходить из более обычных сферических функций, заметив, что по своим свойствам симметрии волновые функции состояний с определен­ными значениями проекции момента на ось  совпадают с собст­венными функциями момента

(103.13)

где ,  — сферические углы в осях , а знак  означает здесь слова «преобразуется как»; комплексное сопряжение в (103.13) связано с измененным знаком в правых сторонах соотношений коммутации (103.3).

Поворот на угол  вокруг оси  (т. е. операция симметрии С₂^()) умножает функцию (103.13) на (—1)^k:

Операцию С₂^() можно рассматривать как результат последова­тельно проведенных инверсии и отражения в плоскости ; пер­вая операция умножает _Jk на (—1)^J, а вторая (изменение знака ) эквивалентна изменению знака k. Учитывая определение функ­ции

_J,-k, получим поэтому

Наконец, при преобразовании С₂^() = С₂^()С₂^() имеем

Учитывая эти законы преобразования, найдем, что состояния, отвечающие функциям (103.12), относятся к следующим типам симметрии:

(103.14)

Путем простого подсчета легко найти число состояний каж­дого типа при заданном значении J. Именно, типу А и каждомуиз типов B₁, B₂, B₃ соответствуют следующие числа состояний

	А	B1, B2, B3,
Четные J	J2 + 1	J2
Нечетные J	(J – 1)2	(J + 1)2

(103.15)

Взаимодействие колебаний и вращения молекулы.

До сих пор мы рассматривали вращение и колебания как независимые движения молекулы. В действительности же одно­временное наличие того и другого приводит к своеобразному взаи­модействию между ними.

Начнем с рассмотрения линейных многоатомных молекул. Линейная молекула может совершать колебания двух типов— продольные с простыми частотами и попереч­ные с двукратными частотами. Нас будут интересовать сейчас последние.

Молекула, совершающая поперечные колебания, обладает, вообще говоря, некоторым моментом импульса. Это очевидно уже из простых механических соображений, но может быть показано и квантовомеханическим рассмотрением. Последнее позволяет также определить и возможные значения этого момента в данном колебательном состоянии.

Предположим, что в молекуле возбуждена какая-либо одна двукратная частота _. Уровень энергии с колебательным кван­товым числом v_a вырожден (v_a + 1)-кратно. Ему соответствует

(v_a + 1) волновых функций

(где _1 + _2 = ) или какие-либо любые их независимые линей­ные комбинации. Общая (по Q_1 и Q_2) старшая степень поли­нома, на который умножается экспоненциальный множитель, во всех этих функциях одинакова и равна _. Очевидно, что всегда

можно выбрать в качестве основных функций линейные комби­нации функций _{1} вида

(104.1)

В квадратных скобках стоит определенный полином, из которого мы выписали только старший член l_а есть целое число, могущее принимать _ + 1 различных значений: l_а =_, _ — 2,

_— 4, ... — _.

Нормальные координаты Q_l, Q_2 поперечного колебания пред­ставляют собой два взаимно перпендикулярных смещения от оси молекулы. При повороте вокруг этой оси на угол  старший член полинома (а с ним и вся функция_l) умножится на

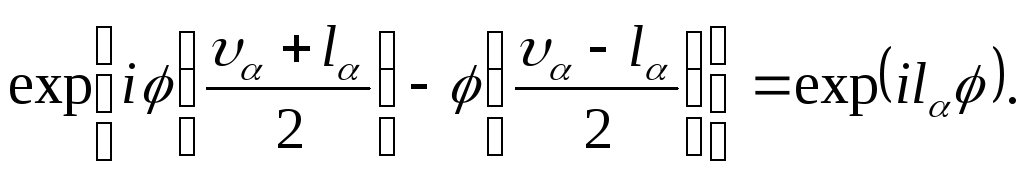
Отсюда видно, что функция (104.1) соответствует состоянию с моментом l_а, относительно оси.

Таким образом, мы приходим к результату, что в состоянии, в котором возбуждена (с квантовым числом _) двукратная ча­стота _, молекула обладает моментом (относительно своей оси), пробегающим значения

l_а = _, _ — 2, _— 4, ... — _.

О нем говорят, как о колебательном моменте молекулы. Если возбуждено одновременно несколько поперечных колебаний, то полный колебательный момент равен сумме l_а. Сложенный с электронным орбитальным моментом, он дает полный момент l молекулы относительно ее оси.

Полный момент импульса молекулы J (как и у двухатомной молекулы) не может быть меньше момента относительно оси, т. е. J пробегает значения

J = l, l+1, ...

Другими словами, состояний с J = 0, 1, ..., l— 1 не сущест­вует.

При гармонических колебаниях энергия зависит только от чисел _ и не зависит от 1_а. Вырождение колебательных уровней (по значениям l_а) снимается при наличии ангармоничности. Сня­тие, однако, неполное: уровни остаются двукратно вырожденными, причем одинаковой энергией обладают состояния, отличающиеся одновременным изменением знака всех 1_а и /; в следующем (после гармонического) приближении в энергии появляется квадратичный по моментам /_а член вида

(g_ — постоянные). Это остающееся двукратное вырождение снимается эффектом, аналогичным - удвоению у двухатомных мо­лекул.

Переходя к нелинейным молекулам, необходимо, прежде всего, сделать следующее замечание чисто механического характера. Для произвольной (нелинейной) системы частиц возникает во­прос о том, каким образом можно вообще отделить колебательное движение от вращения, другими словами, что следует понимать под «невращающейся системой». На первый взгляд, можно было бы подумать, что критерием отсутствия вращения может являться равенство нулю момента импульса:

m[rv] = 0 (104.3)

(суммирование по частицам системы). Однако стоящее слева вы­ражение не является полной производной по времени какой-либо функции координат. Поэтому написанное равенство не может быть проинтегрировано по времени так, чтобы быть сформулированным в виде равенства нулю некоторой функции координат. Между тем именно это необходимо для того, чтобы можно было разум­ным образом сформулировать понятие о «чистых колебаниях» и «чистом вращении».