- •Физика атома, атомного ядра и элементарных
- •Одномерная прямоугольная потенциальная яма ("ящик")
- •Одномерная прямоугольная потен- циальная яма (ящик) с бесконечно высокими стенками
- •В этом случае внутри ямы частица дви- жется свободно, но выйти за ее
- •Стационарное уравнение Шредингера
- •Таким образом, собственными функция-ми
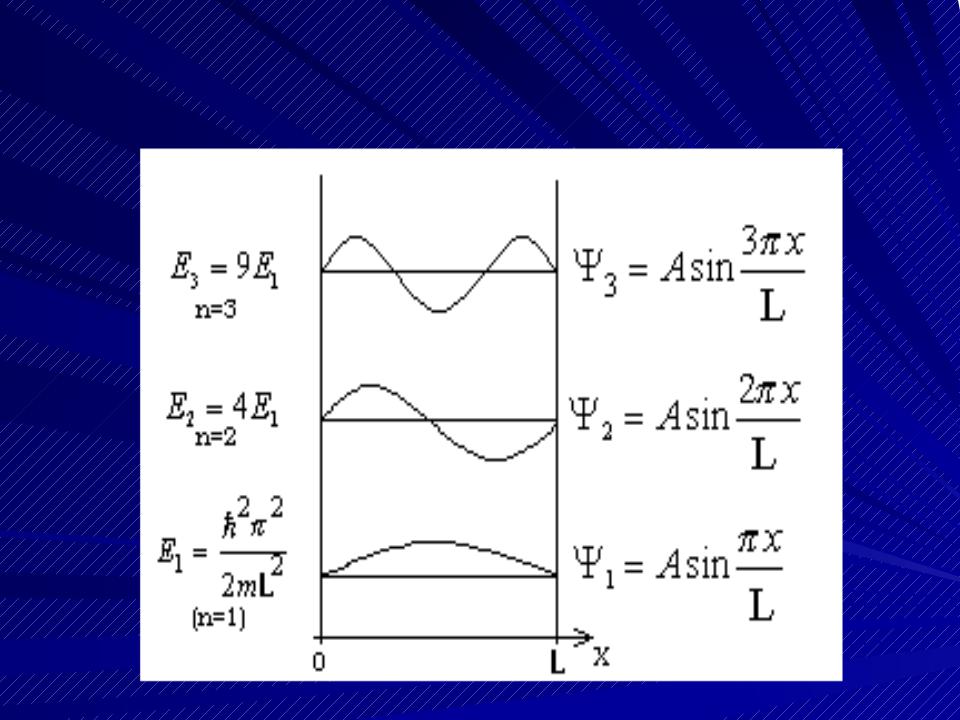
- •Таким образом, частица (например, электрон) в потенци- альной яме может иметь не произвольные,
- •Графики первых трех собственных функций
- •Плотность вероятности распределения частиц
- •Этот результат резко отличается от клас- сического: в классической механике на- хождение частицы
- •Интернет-экзамен
- •Интернет-экзамен

Физика атома, атомного ядра и элементарных
частиц
9 (2). Простейшие задачи квантовой  механики.
механики. 
Частица в "потенциальной яме" ("ящике")
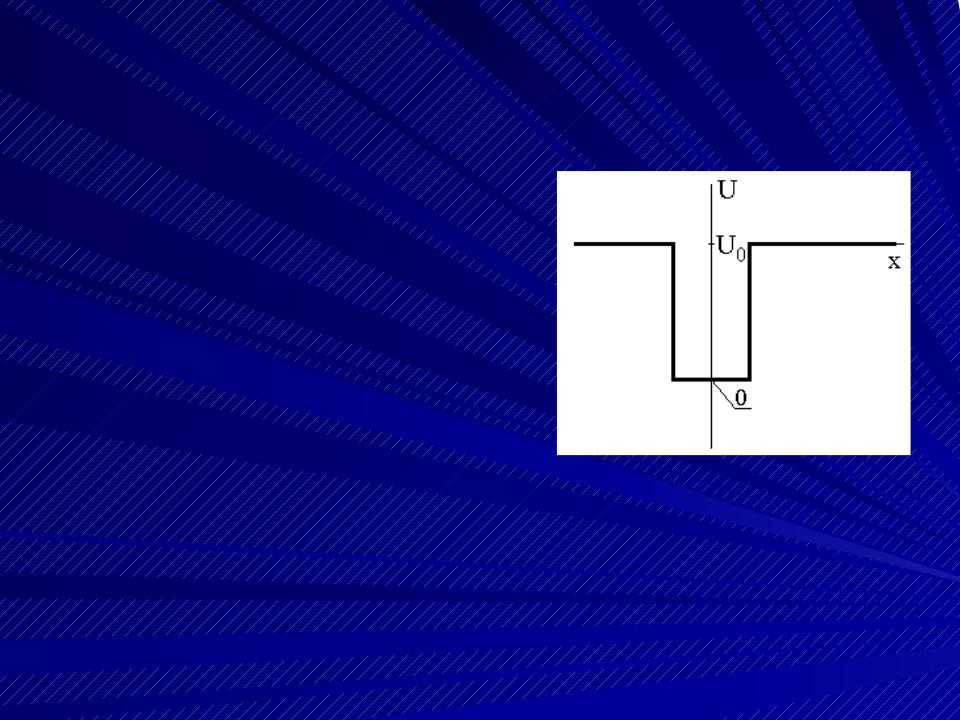
Одномерная прямоугольная потенциальная яма ("ящик")
Так называется одномер- ная область, в которой потенциальная энергия имеет вид, изображен- ный на рисунке. Для этой области легко получить точное решение уравне- ния Шредингера и рас- смотреть задачу о кван- товании энергии.
Потенциальная энер- гия равна нулю на дне ямы ("ящика"), и равна U0 вне сте- нок "ящика".

Одномерная прямоугольная потен- циальная яма (ящик) с бесконечно высокими стенками
 Наиболее простым в мате- матическом отношении яв- ляется решение для потен- циальной ямы с бесконечно высокими стенками. Иногда ее называют ямой с идеаль- но отражающими стенками.
Наиболее простым в мате- матическом отношении яв- ляется решение для потен- циальной ямы с бесконечно высокими стенками. Иногда ее называют ямой с идеаль- но отражающими стенками.
0, 0 x L U , x 0, x L
Ширина ямы (ящика) рав- на L, на дна ямы потен- циальная энергия равна нулю, высота стенок бес- конечно велика.

 В этом случае внутри ямы частица дви- жется свободно, но выйти за ее преде- лы не может, т.е. за пределами ямы волновая функция должна обратиться в нуль. Но волновая функция должна быть непрерывна, поэтому она должна быть равна нулю в точках x = 0 и x = L:
В этом случае внутри ямы частица дви- жется свободно, но выйти за ее преде- лы не может, т.е. за пределами ямы волновая функция должна обратиться в нуль. Но волновая функция должна быть непрерывна, поэтому она должна быть равна нулю в точках x = 0 и x = L:
(0) (L) 0 |
(9.1) |
- это граничные условия для волновой функции . 

 Стационарное уравнение Шредингера
Стационарное уравнение Шредингера
(8.6) |
2m |
|
|
h2 |
(E U ) 0 |
внутри ямы принимает вид (т.к. U = 0):
d 2 2m |
E 0 |
|
dx2 h2 |
(9.2) |
Общее решение этого уравнения хорошо известно:
(x) Asin |
2Em x B cos |
2Em x (9.3) |
|
h |
h |

Из условия (9.1) (0) =0 следует, что B = 0. Из второго граничного условия (L) =0
следует, что |
Asin |
2Em |
L |
0 |
||
откуда |
|
h |
|
|||
2Em |
|
|
|
|
||
|
L n |
|
||||
|
h |
|
|
|||
или |
2Em |
n |
|
(9.4) |
||
h |
|
L |
||||
|
|
|
||||
где n = 1, 2, 3, ... - целое число 

Таким образом, собственными функция-ми
уравнения Шредингера в рассматри- |
|
|||
ваемой задаче являются волновые |
|
|||
функции вида |
|
|
x |
|
|
n |
A sin n |
(9.5) |
|
|
n |
L |
||
|
|
|
|
|
Собственные значения энергии найдем из
формулы (9.4): |
2h2 |
|
|
En |
n2 |
(9.6) |
|
|
2mL2 |
|
|
- дискретный спектр собственных значений энергии. 

Таким образом, частица (например, электрон) в потенци- альной яме может иметь не произвольные, а лишь дис- кретные, квантованные значения энергии.
Рассмотрим некоторые свойства собственных функций. 1). Собственные функции, принадлежащие различным
собственным значениям, ортогональны, т.е.
m x n x dx 0
Доказательство
|
nx |
sin |
mx |
dx |
1 |
L |
x |
(m n) cos |
x |
|
An Am sin |
L |
L |
2 |
An Am cos |
L |
L |
(m n) dx 0 |
|||
|
|
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(9.7) |
если m ≠ n |
|
|
|
|
|
|
|
|
|
|

Если m = n, то интеграл (9.7) не равен 0, и из условия нормировки можно найти коэффициент An:
|
2 |
|
|
2 |
|
|
2 nx |
|
1 |
l |
|
|
2 nx |
|
|
n |
dx 1 |
n |
|
sin |
|
dx |
|
n |
|
|
|
||
|
|
A |
|
|
L |
2 |
A |
1 cos |
L |
dx |
||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
1 |
A2 L 1 A |
|
2 |
|
|
|||||
|
|
|
|
|
2 |
n |
|
|
|
n |
|
L |
|
|
т.е. нормирующий множитель у всех собст- венных функций одинаков. Поэтому
венных функций одинаков. Поэтому
n |
2 sin |
nx |
(9.8) |
|
L |
L |