Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 12

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 12

– стандартизованная нормальная величина.

Функция распределения стандартизованной нормальной величины.

Пример.

Дана СВ Х, . Найти вероятность попадания .

Решение.

Часто требуется вычислять вероятность того, что отклонение нормально распределенной СВ Х от МО по абсолютной величине меньше заданного положительного числа .

– ?

Методами математического анализа можно легко построить график плотности

Гауссова кривая:

S = 1

m – сдвиг по оси 0Х

 – параметр островершинности

Замечание.

Мода и медиана совпадают с МО.

§ 4. Оценка отклонения теоретического распределения от нормального; асимметрия и эксцесс

При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики (асимметрию и эксцесс).

Для нормального распределения эти характеристики равны 0, поэтому, если для изучаемого теоретического распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость этого распределения к нормальному. Наоборот большие значения и , указывают значительные отклонения от нормального.

Пологая часть правее моды, значит .

Пологая часть левее моды, значит .

Замечание.

При исследовании эксцесса надо считать, что нормальное исследуемое распределение, имеют одинаковое МО и дисперсию.

Глава VII. Системы случайных величин (случайные векторы)

Пусть на одном и том же вероятностном пространстве (,A, P) задано n СВ, , совокупность – называется многомерной (n-мерной) СВ или случайным вектором.

Примеры.

Широта X и долгота Y падения метеорита на Землю представляет собой двумерный случайный вектор . В эту модель можно ввести третью координату Z – это время от начала наблюдения до падения первого метеорита на Землю. Тогда .

Успеваемость студента, окончившего курс обучения в ВУЗе, характеризуется n – случайных величин, проставленных по 5-ти бальной системе.

§ 1. Совместная функция распределения

Рассмотрим в одном и том же вероятностном пространстве (,A,P) набор СВ . Так как множество A, таких пересечения A, поэтому существует вероятность этого события, которая называется многомерной функцией распределения.

.

Замечания:

1.В дальнейшем ограничимся случаем двух случайных величин .

2. Функция – вероятность того, что случайная точка попадает в бесконечный квадрант с вершиной в точке .

С помощью F, можно вычислить вероятность попадания случайной точки в полуполосу или в прямоугольник.

а)

б)

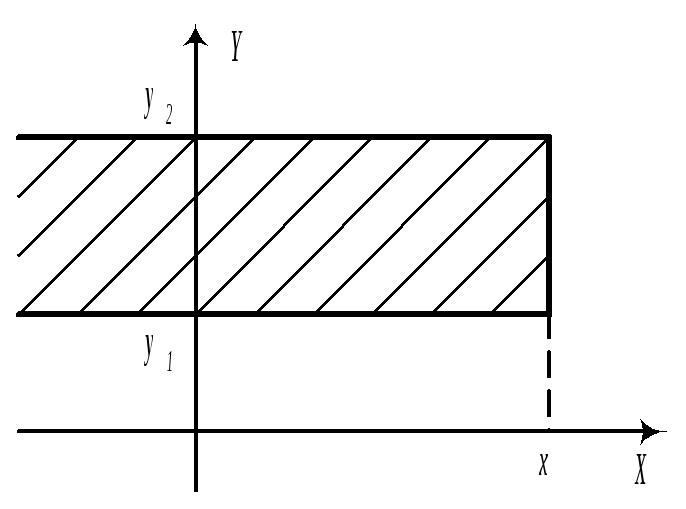
в)

Пример.

Решение

Из формулы вероятности попадания в прямоугольник и определения многомерной функции распределения , вытекают следующие свойства, которые доказываются аналогично одномерному случаю.

Свойства.

1. по каждому аргументу не убывает и непрерывна слева.

2. .

3. .

4. а) При становится функцией распределения компоненты x.

.

б) При становится функцией распределения компоненты y.

.

§ 2. Дискретные двумерные случайные величины

Определение. Двумерная СВ (X, Y) называется дискретной, если каждая из СВ и Х и Y является дискретной.

Пусть СВ Х может принимать значения , а СВ Y принимает дискретные значения .

Y X	y1	y2	…	ym	P{X=xi}
x1	P11	P12	…	P1m	P1
x2	P21	P22	…	P2m	P2
…	…	…	…	…	…
xn	Pn1	Pn2	…	Pnm	Pn
P{Y=yj}	P1	P2	…	Pm	

Двумерный случайные вектор может принимать только пары значений

По этой таблице нетрудно определить функцию распределения.

.