Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный морской технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

razdel_1_konspekta_lektsy.pdf

Скачиваний:

Добавлен:

18.04.2015

Размер:

993.48 Кб

Скачать

☆

<<< < Предыдущая 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 4344 / 4444

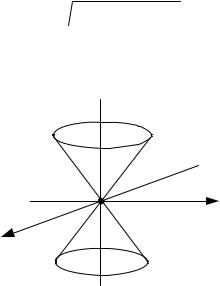
Из уравнения ясно, что поверхность симметрична относительно координатных осей. При сечении поверхности плоскостями z = ±h получаются эллипсы

x2	+	y2	=	h2	x2		+	y2		=1
				или
						2			2
a2		b2		c2	a2	h		b2	h
						c2			c2

с полуосями ahc и bhc .

Если же пересекать поверхность плоскостями x = ±h или y = ±h , то в сечении получим гиперболы

z 2

−

Если ее пересекать плоскостями y = ±hx , то в сечении получим пару пересекающихся прямых

z = ±cx(1/ a2 )+ (h2 / b2 ).

Уравнению удовлетворяет точка (0,0,0), следовательно, поверхность проходит через начало координат. Вид поверхности показан на рисунке 1.7.14.

Рис. 1.7.14.

Цилиндры второго порядка

Определение 1.7.3

Поверхность, описываемая прямой, параллельной некоторому заданному направлению и пересекающей данную линию L, называется цилиндрической. При этом движущаяся прямая называется образующей, а прямая L - направляющей цилиндра.

Если образующая цилиндра параллельна какой-то из координатных осей, то цилиндрическая поверхность задается уравнением второго порядка с двумя переменными:

F(x, y)= 0 , образующая параллельна оси Oz ;

F(x, z)= 0 , образующая параллельна оси Oy ;

F(y, z)= 0 , образующая параллельна оси Ox .

Эллиптический цилиндр

		x2		y2			(a,b > 0) .
			+			=1
		a2	+	b2		=1
		a2		b2
Уравнение	не содержит переменной			z , следовательно, цилиндр параллелен оси Oz .
Направляющей	цилиндра на плоскости				xOy		является эллипс с полуосями a и b .
					75

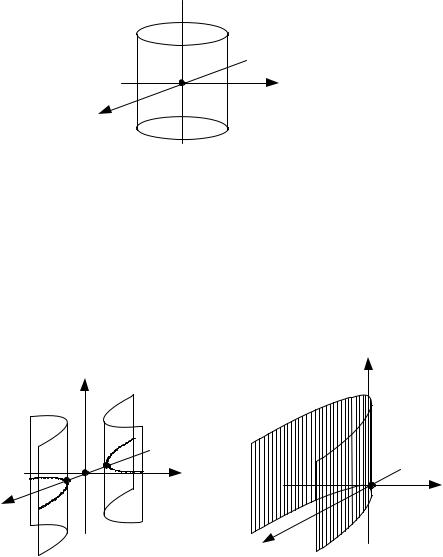
Цилиндрическая поверхность, описанная прямой, параллельной оси Oz , и пересекающей эллипс

x2	+	y2	=1	, построена на рисунке 1.7.15.
a2		b2

O	y
	y
x

				Рис. 1.7.15.
Гиперболический и параболический цилиндры
	x2	−	y2	=1 (a,b > 0) и y2	= 2 px ( p > 0) .
	a2	−		=1 (a,b > 0) и y2	= 2 px ( p > 0) .
	a2		b2
В данном случае направляющими линиями поверхностей являются гипербола						x2	−	y2	=1 и
						a2	−	b2	=1 и
						a2		b2

парабола y2 = 2 px , а образующими — прямые, параллельные оси	Oz и проходящие через
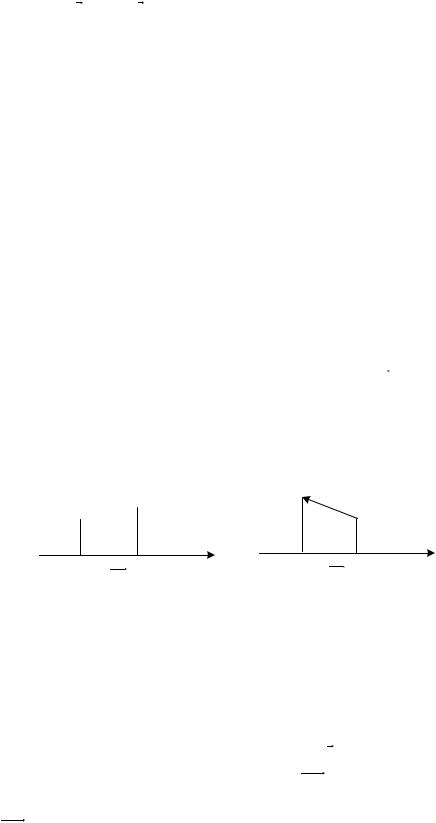
гиперболу или параболу в плоскости xOy . Поверхности изображены на	рисунках 1.7.16 и 1.7.17.

z		z
z
O	y	O	y
	y
x
x
		x
Рис. 1.7.16.		Рис. 1.7.17.

концом в точке

Если коллинеарны два ненулевых вектора,

то

их координаты пропорциональны, т.е. для

коллинеарных векторов a =

b = y2

условие коллинеарности принимает вид:

Задача 1.3.1

		r		p		r
Выясните, при каких значениях	p и q	r		1		r
Выясните, при каких значениях	p и q	векторы a	=	1	и b
				− 2
				− 2

=q коллинеарны.

−1

Решение

Из условия коллинеарности векторов следует

− 2

= 2 или

= 2,

= 2 а тогда

−1

p = 4, q =

1.3.4. Проекция вектора на числовую ось. Декартова система координат. Линейные операции над векторами в R3 .

Рассмотрим числовую ось Ox и вектор (направленный отрезок) AB (рис. 1.3.1). Проекцией вектора на числовую ось называют длину отрезка этой оси между проекциями конечной и начальной точек вектора на ось, если вектор и ось направлены в одну сторону. Если вектор и ось направлены в разные стороны, то проекцией вектора на ось называется длина отрезка оси между проекциями конечной и начальной точек вектора, взятая со знаком минус (рис. 1.3.1).

B B

A A

_____

O 123

_____

x O 123

ПрOx AB >0

ПрOx AB <0

Рис. 1.3.1.

В трехмерном пространствеR3 , являющемся частным случаем конечномерного векторного пространства Rn , введем прямоугольную декартову систему координат.

r		1		r		0	r		0
r		0		r		1	r		0
Для этого векторы i	=	0	,	j	=	1	и k	=	0	, образующие в пространстве R3 базис,
		0				0			1
		0				0			1

изобразим взаимно перпендикулярными отрезками единичной длины, направленными вдоль координатных осей Ox, Oy, Oz соответственно. Тогда вектор a = xir+ yrj + zk пространства R3 ,

разложенный по этому базису, можно изображать отрезком OM с началом в начале координат и с M (x, y, z) (рис.1.3.2). Координаты вектора a в такой системе координат являются

проекциями OM или точки M на координатные оси.

	zi	M
		M
		r
		a
	k
i	O	j	yj
				y


xiv
x
		Рис.1.3.2.
ЗАМЕЧАНИЕ
Для векторов из пространства R3 часто используют			обозначение: a = {x; y; z}, где x, y, z -

координаты вектора.

Начало направленного отрезка, являющегося изображением вектора a может параллельным переносом помещаться в любую точку пространства. Проекции вектора на координатные оси при этом не изменятся. Если начало направленного отрезка в точке A(x1; y1; z1), а конец в точке B(x2; y2; z2 ), то соответствующий вектор ar = AB = {x2 − x1; y2 − y1; z2 − z1}(рис. 1.3.3)

z z2

z1 A B

O	y1	y2
x1		y

Рис. 1.3.3.

В следующей таблице собраны формулы для нахождения координат линейных операций над

векторами трехмерного пространства R3 .

Сложение

	r	x	x				x	+ x
ar	r	1			2		1		2
ar	+b	= y1		+ y2			= y1 + y2				.
		z	z		2		z	+ z	2
		1			2		1		2
Вычитание
	r	x		x			x	− x		2
ar	r	1				2	1			2
ar	−b	= y1		− y2			= y1 − y2
		z		z		2	z	− z		2
		1				2	1			2

r
a	r	+b				b	r
	a	+b		a		b
				r
		r			r	r
		b			r	r
					a	+b
				r
				a	r
					r
			r		b
			r	r	−
		b		a
		b

Умножение на число

λ ar

λ x

λa

= λ y1

λ y1

λ < 0

r λ > 0

λ z1

Базис в пространстве

R 3

образуют

любые три линейно независимых

(некомпланарных)

вектора.

Тройка некомпланарных векторов называется правой (базисом с правой ориентацией), если из конца третьего вектора вращение от первого к второму происходит против часовой стрелки.

Если из конца третьего вектора вращение от первого к второму происходит по часовой стрелке, то тройка некомпланарных векторов называется левой (базисом в правой ориентацией)

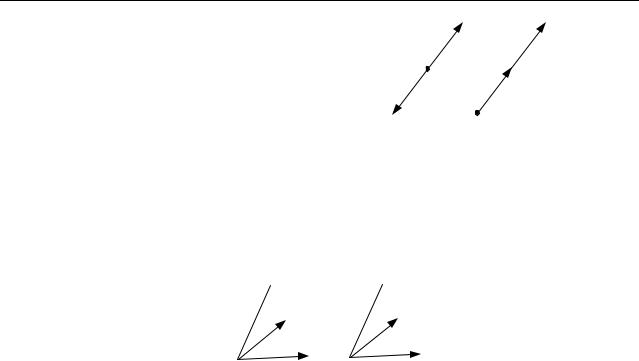
На рисунке 1.3.4 a тройка векторов ar, b, cr – правая, а на рисунке 1.3.4 b – левая.

c c

b	a
b
a	b
a
Рис. 1.3.4 a.	Рис. 1.3.4 b.
ЗАМЕЧАНИЕ 1
Из рисунка 1.3.3 ясно, что тройка векторов i , j, k	правая, а показанная на этом рисунке система
координат (поворот от одной оси к последующей,	от Ox к Oy , от Oy к Oz и от Oz к Ox .

происходит против часовой стрелки) задает правую ориентацию пространства.