7.15. Математическое ожидание дискретной случайной величины
В статистике, как только что было получено, среднее арифметическое по известным результатам n опытов вычисляется так
Начнём неограниченно увеличивать число опытов
n
При этом частота каждого возможного значения случайной величины сходится к некоторому числу, называемому и являющемуся вероятностью этого значения
.
А выражение для среднего арифметического переходит в выражение математического ожидания дискретной случайной величины
В этом выражении вместо частот стоят вероятности значений, а в обозначении результата опущена буква n.
N (большое) – это, по-прежнему, количество возможных значений.
–значения
дискретной случайной величины.
–значения закона
распределения дискретной случайной
величины.
Математическое ожидание дискретной случайной величины вычисляется как сумма произведений всех значений случайной величины на их вероятности.
Смысл математического ожидания: математическое ожидание – это среднее значение случайной величины.
В теории вероятности математическое ожидание дискретной случайной величины вычисляется без проведения каких-либо опытов по известным значениям закона распределения. Поэтому его другое название – теоретическое среднее.
Вычислим математическое ожидание для какого-нибудь простого случая: например, для опыта с монетой.
«Орлу» мы ставили в соответствие 0, а «решке» – 1.
Закон распределения для монеты, мы помним, выглядит так:
Вычисляем математическое ожидание. У нас всего два возможных значения, следовательно меняется от 1 до 2.
i=1 соответствует «орёл», т.е. 0, а i=2 – «решка», т.е. 1. Вероятности этих обоих значений одинаковы и равны 0.5.
M(X) = P(x1) x1 + P(x2) x2 = 0.5 0 + 0.5 1 = 0.5
Получилось 0.5. Что это такое за значение?
Это значение лежит посередине между значениями нашей случайной величины.
Теперь более сложный двусторонний предмет.
Представим, что у нас небьющееся блюдце. При падении такого предмета выпадение разных сторон уже не будет равновероятным. Упав на выпуклое дно, блюдце может ещё перевернуться через край; а упав вверх дном, оно, скорее всего, останется в этом положении.
Будем считать, что нам известно точно, что в положении «вверх дном» блюдце успокаивается ровно в 2/3 случаев, а в положении «на дне» – 1/3 случаев.
Положению «вверх дном» припишем значение 0; а положению «на дне» – 1.
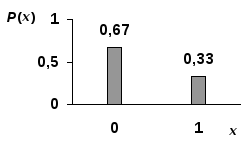
Вычислим математическое ожидание такого закона распределения.
M(X) = P(x1) x1 + P(x2) x2 = 2/3 0 + 1/3 1 = 1/3.
Видим, что, если получившееся значение отметить на горизонтальной оси, то оно окажется ближе к более высокому столбику. А если мы представим, что, чем выше столбик, тем он тяжелее, то математическое ожидание будет расположено ближе к более тяжёлому столбику.
И сейчас мы узнаем одно из свойств математического ожидания.
Представим такой опыт: на невесомой линейке в точках, равных значениям случайной величины, размещены гирьки с весами, пропорциональными вероятностям соответствующих значений.
0 1
Если теперь подвести под линейку опору в точке математического ожидания, то получившиеся качели или весы окажутся в равновесии.
Точка математического ожидания находится под центром тяжести таких весов.
Любопытно то, что даже если закон распределения будет сложнее, т.е. будет состоять из многих столбиков, картина будет той же.
Таким образом, математическое ожидание дискретной случайной величины соответствует абсциссе центра тяжести закона распределения. Абсцисса – это координата на горизонтальной оси.
И ещё об одном понятии, которое будет использоваться в дальнейшем.
Суммирование каких-либо значений с множителями, равными их вероятностям, как при вычислении математического ожидания, называется операцией усреднения.