7.13. Равномерно и нормально распределённые случайные величины

В качестве примера дискретных случайных величин нами была рассмотрены: бросание кубика, бросание монеты.

Рассмотрим теперь примеры непрерывных случайных величин.

Равномерно распределённая случайная величина.

Плотность распределения такой случайной величины есть функция, отличная от нуля только в пределах отрезка от a до b.

Е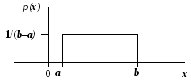ё уровень в пределах отрезка отa до b постоянен и обратно пропорционален длине отрезка:

Равномерно распределённая случайная величина наиболее проста для понимания и описания.

Также как на рисунке выглядит слой, который образуют случайно вылетающие из распылителя капельки краски при нанесении изображения через трафарет.

Равномерное распределение имеют ошибки округления при измерениях или вычислениях.

Например, взвешиваем образец товара из проверочной закупки. Его масса может принимать любое значение, но мы, глядя, на шкалу весов, определяем ближайшее деление. Ошибка снятия показаний по шкале имеет равномерное распределение.

Эта случайная величина будет использоваться нами в практических работах.

Нормально распределённая случайная величина.

Примером нормально распределённой случайной величины является координата попадания шарика на ось в опыте с доской Гальтона, который рассматривался нами в вопросе «Первые статистические опыты».

Ещё говорят, что такая случайная величина имеет нормальное распределение.

Случайные величины с нормальным распределением имеют исключительно широкое распространение в природе.

Отсюда и название: нормальное, что значит типовое, характерное.

Математическая запись нормальной плотности распределения следующая (формула страшная):

, для .

Здесь  = 3,14…, е = 2,72… – основание натурального логарифма.

Параметрами нормального распределения являются величины m и , имеющие специальные названия:

m – математическое ожидание или среднее;

–дисперсия или рассеяние (обозначается маленькой греческой буквой «сигма»).

Более подробно смысл этих понятий будет объяснён позже.

На графике плотность распределения вероятности нормально распределённой случайной величины выглядит как колоколообразная кривая.

Это знакомая нам огибающая уровней шариков в ячейках в опыте Гальтона.

Вершина распределения имеет абсциссу, равную математическому ожиданию x = m.

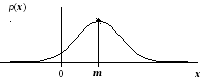
Площадь, заключённая между кривой и горизонтальной осью равна 1.

7.14. Среднее арифметическое

Закон распределения или плотность распределения вероятности несёт полную информацию о случайной величине.

На практике довольно часто требуется сравнить две случайные величины. Сравнение распределений подразумевает сравнение каких-либо их существенных черт. Удобно, чтобы они выражались числами, тогда сравнение становится совсем простым.

Поэтому хотелось бы иметь числовые характеристики, которые описывали бы как закон распределения, так и плотность вероятности, причём любого вида.

Наиболее простыми и практически важными числовыми характеристиками случайной величины являются математическое ожидание (среднее) и дисперсия (рассеяние).

Математическое ожидание случайной величины Х является вероятностным обобщением понятия среднего арифметического, которое применяется в статистике. С него и начнём.

Вначале рассмотрим дискретную случайную величину Х с N возможными значениями. (У кубика – 6 возможных значений.)

Пусть с этой случайной величиной проделано n одинаковых опытов («эн» маленькое).

При этом случайная величина Х (икс большое)

значение принялараз, т.е.–

значение принялараз, т.е.–

и так далее …,

значение принялараз, т.е.–.

Общее количество появления всех значений равно n, т.е.

Найдём среднее арифметическое случайной величины Х по n опытам.

Среднее арифметическое – это, как известно, сумма всех значений, делённая на их количество:

.

Преобразуем это выражение, учтя повторяемость значений:

Теперь для сокращения длины формулы воспользуемся специальным знаком суммы, который мы уже рассматривали,

Дробь в каждом слагаемом – это вычисленная по n опытам частота события, состоящего в том, что случайная величиной Х примет значение . Мы её обозначали так:.

В итоге получаем:

Так, введя некоторые обозначения, мы преобразовали выражение для среднего арифметического.

Из полученного выражения видно, что среднее арифметическое вычисляется как сумма значений случайной величины, взятых с множителями, в качестве которых выступают частоты.