Условие принадлежности двух прямых к одной плоскости.

Прямые лежат в одной плоскости. если они 1) пересекаются;2) параллельны.

Для принадлежности прямых L₁: 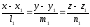и L₂: одной плоскости  чтобы векторы М₁М₂={x₂-x₁;y₂-y₁;z₂-z₁}, q₁={l₁;m₁;n₁} и q₂={l₂;m₂;n₂} были компланарны. Т.е., по условию компланарности трех векторов, смешанное произведение М₁М₂·s₁·s₂=Δ==0(8)

Т.к. условие параллельности двух прямых имеет вид: 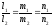, то для пересечения прямыхL₁ и L₂ , чтобы они удовлетворяли условию (8) и чтобы нарушалась хотя бы одна из пропорций .

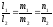Пример. Исследовать взаимное расположение прямых:

L₁: , L₂:

Направляющий вектор прямой L₁–q₁=(1;3;-2). Прямая L₂ задана как пересечение 2-х плоскостей α₁: х-у-z+1=0; α₂: x+y+2z-2=0. Т.к. прямая L₂ лежит в обеих плоскостях, то она, а значит и ее направляющий вектор, перпендикулярна нормалям n₁ и n₂. Следовательно, направляющий вектор s₂ является векторным произведением векторов n₁ и n₂, т.е. q₂ =n₁ х n₂==-i-3j+2k.

Т.о. s₁=- s₂, значит прямые или параллельны, или совпадают.

Чтобы проверить совпадают ли прямые, подставим координаты точки М₀(1;2;-1)L₁ в общие уравнения L₂: 1-2+2+1=0 – неверные равенства, т.е. точка М₀ L_2,

1+2+4-2=0

следовательно прямые параллельны.

Расстояние от точки до прямой.

Расстояние от точки М₁(х₁;у₁;z₁) до прямой L, заданной каноническим уравнением L: можно вычислить при помощи векторного произведения.

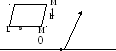Из канонического уравнения прямой следует, что точка М₀(х₀;у₀;z₀)L, а направляющий вектор прямойq=(l;m;n)

Построим параллелограмм на векторах q и М₀М₁. Тогда расстояние от точки М₁ до прямой L равно высоте h этого параллелограмма. Т.к. S=|qxМ₀М₁|=h|q|, то

h=(9)

Расстояние между двумя прямыми в пространстве.

L₁: 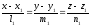и L₂:

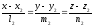
1) L₁L₂.

d=

2) L₁ и L₂ – скрещивающиеся

d=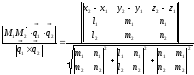

Взаимное расположение прямой и плоскости в пространстве.

Для расположения прямой и плоскости в пространстве возможны 3 случая:

• прямая и плоскость пересекаются в одной точке;

• прямая и плоскость параллельны;

• прямая лежит в плоскости.

Пусть прямая задана своим каноническим уравнением, а плоскость – общим

L: ,

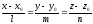α: Ах+Ву+Сz+D=0

Уравнения прямой дают точку М₀(х₀;у₀;z₀)L и направляющий векторq=(l;m;n), а уравнение плоскости – нормальный вектор n=(A;B;C).

1. Пересечение прямой и плоскости.

Если прямая и плоскость пересекаются, то направляющий вектор прямой q не параллелен плоскости α, а значит не ортогонален нормальному вектору плоскости n. Т.е. их скалярное произведение n·q≠0 или, через их координаты,

Am+Bn+Cp≠0 (10)

Определим координаты точки М - точки пересечения прямой L и плоскости α.

Перейдем от канонического уравнения прямой к параметрическому: , tR

Подставим эти соотношения в уравнение плоскости

А(x₀+lt)+B(y₀+mt)+C(z₀+nt)+D=0

A,B,C,D,l,m,n,x₀,y₀,z₀ – известны, найдем параметр t:

t(Al+Bm+Cn)= -D-Ax₀-By₀-Cz₀

если Am+Bn+Cp≠0, то уравнение имеет единственное решение, определяющее координаты точки М:

t_М= -→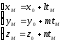(11)

Угол между прямой и плоскостью. Условия параллельности и перпендикулярности.

Угол φ между прямой L:

с направляющим вектором q={l;m;n} и плоскостью

: Ах+Ву+Сz+D=0 с нормальным вектором n=(A;B;C) находится в пределах от 0˚ ( в случае параллельности прямой и плоскости) до 90˚ (в случае перпендикулярности прямой и плоскости). (Угол между вектором q и его проекцией на плоскость α).

– угол между векторами q и n.

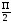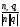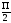Т.к. угол  между прямой L и плоскостью  является дополнительным к углу , то sin φ=sin(-)=cos =- (рассматривается абсолютная величина т.к. угол φ острый sin φ=sin(-) или sin φ=sin(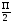+) в зависимости от направления прямой L)

sin φ=(12)