
- •Уравнение поверхности в пространстве.
- •Классификация поверхностей.
- •Плоскость в пространстве.
- •Неполные уравнения плоскости.
- •Уравнение плоскости, проходящей через три заданные точки.
- •(4) Уравнение плоскости, проходящей через 3 заданные точки.
- •Уравнение плоскости в отрезках на осях.
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.
- •Нормированное (нормальное) уравнение плоскости.
- •Пучки и связки плоскостей.
- •Прямая в пространстве.
- •Общие уравнения прямой в пространстве.
- •Канонические уравнения прямой.
- •Параметрические уравнения прямой.
- •Условие принадлежности двух прямых к одной плоскости.
- •Расстояние от точки до прямой.
- •Расстояние между двумя прямыми в пространстве.
- •Взаимное расположение прямой и плоскости в пространстве.
- •1. Пересечение прямой и плоскости.
- •Угол между прямой и плоскостью. Условия параллельности и перпендикулярности.
- •Условие параллельности прямой и плоскости.
Уравнение поверхности в пространстве.
Пусть заданы декартова прямоугольная система координат Охуz в пространстве и некоторая поверхность S.
Определение. Уравнение F(x;y;z)=0 (7) называется уравнением поверхности S (относительно заданной системы координат), если этому уравнению удовлетворяют координаты х,у, z любой точки, лежащей на поверхности S, и не удовлетворяют координаты х, y и z ни одной точки, не лежащей на поверхности S.
Т.о. поверхностью называется геометрическое место точек {M(x;y;z)}, координаты которых удовлетворяют уравнению (7).
Уравнение (7) определяет поверхность S.
z=f(x;y) (8) – явное уравнение линии в ДСК
(Уравнение (8) может быть получено из уравнения (7) путем выражения из этого уравнения одной переменной через другие.
 Если
уравнение (7) не содержит какой-либо
координаты х,у или z, то получаем уравнение
цилиндрической поверхности, которая
параллельна оси, соответствующей
отсутствующей переменной. F(x;y)=0
Если
уравнение (7) не содержит какой-либо
координаты х,у или z, то получаем уравнение
цилиндрической поверхности, которая
параллельна оси, соответствующей
отсутствующей переменной. F(x;y)=0
x2+y2=R2
Пример. Уравнение сферы.
Сферой в пространстве называется множество точек равноудаленных от заданной точки М0(х0;у0;z0) – центра сферы.
Пусть М(х;у;z) – некоторая переменная точка сфера. Расстояние от точки М до центра М0 постоянно и равно радиусу сферы, т.е. d(M0M)=const=R
R=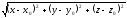
R2=(x-x0)2+(y-y0)2+(z-z0)2 – уравнение сферы.
Уравнения линия в пространстве R3.
Линия в пространстве определяется как пересечение двух поверхностей, т.е. как геометрическое место точек, находящихся одновременно на двух поверхностях.
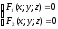 (9)
– общее уравнение линии в пространстве.
(9)
– общее уравнение линии в пространстве.
Линию как пересечение двух поверхностей в пространстве можно представить бесчисленным числом способов. Т.е. вместо системы (9) можно взять любую эквивалентную систему.
Параметрические уравнения линии и поверхности в пространстве.
Линию в пространстве можно так же задать параметрически:
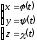 (10)
где функции
(t),
(t)
и (t)
определены и непрерывны в некотором
промежутке изменения параметра t.
(10)
где функции
(t),
(t)
и (t)
определены и непрерывны в некотором
промежутке изменения параметра t.
Покажем, что этот способ определения линии в пространстве эквивалентен определению линии как пересечения двух поверхностей.
Допустим, что хотя бы одна из трех функций, например (t), имеет обратную. Тогда t=-1(z) подставляя это значение вместо t в первые два равенства (10), получим уравнения двух поверхностей x=(-1(z)), y=(-1(z)),
пересечением которых является данная линия. Пример (с.115).
Классификация поверхностей.
Определение 1. Поверхность называется алгебраической, если в некоторой декартовой прямоугольной системе координат, если она определяется алгебраическим уравнением F(x;y;z)=0 с тремя переменными.
Определение 2. Всякая не алгебраическая поверхность называется трансцендентной.
Определение 3. Алгебраическая поверхность называется поверхностью порядка n, если в некоторой декартовой прямоугольной системе координат она определяется алгебраическим уравнением степени n с тремя переменными.
Установлению корректности определений 1,2,3 способствует следующая теорема.
Теорема (док-во на с.117). Если поверхность в некоторой декартовой прямоугольной системе координат определяется алгебраическим уравнением степени n, то эта поверхность и в любой другой декартовой прямоугольной системе координат определяется алгебраическим уравнением той же степени n.
