
- •Уравнение поверхности в пространстве.
- •Классификация поверхностей.
- •Плоскость в пространстве.
- •Неполные уравнения плоскости.
- •Уравнение плоскости, проходящей через три заданные точки.
- •(4) Уравнение плоскости, проходящей через 3 заданные точки.
- •Уравнение плоскости в отрезках на осях.
- •Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.
- •Нормированное (нормальное) уравнение плоскости.
- •Пучки и связки плоскостей.
- •Прямая в пространстве.
- •Общие уравнения прямой в пространстве.
- •Канонические уравнения прямой.
- •Параметрические уравнения прямой.
- •Условие принадлежности двух прямых к одной плоскости.
- •Расстояние от точки до прямой.
- •Расстояние между двумя прямыми в пространстве.
- •Взаимное расположение прямой и плоскости в пространстве.
- •1. Пересечение прямой и плоскости.
- •Угол между прямой и плоскостью. Условия параллельности и перпендикулярности.
- •Условие параллельности прямой и плоскости.
Пучки и связки плоскостей.
Определение. Совокупность всех плоскостей, проходящих через одну и ту же прямую L, называется пучком плоскостей (с центром в L).
Теорема. (б.д.?)Если A1x+В1у+С1z+D1=0 и A2x+В2у+С2z+D2=0 уравнения двух различных непараллельных плоскостей, пересечением которых служит некоторая прямая L, а и - произвольные числа такие, что 2+20, то
(A1x+В1у+С1z+D1)+(A2x+В2у+С2z+D2)=0 (15)
уравнение плоскости, проходящей через прямую L.
Какова бы ни была проходящая через прямую L плоскость, она определяется уравнением (15) при некоторых и .
Определение. Совокупность всех плоскостей, проходящих через одну и ту же точку М0(х0;у0;z0), называется связкой плоскостей (с центром в М0).
Уравнение связки с центром в точке М0(х0;у0;z0) имеет вид
А(х-х0)+В(у-у0)+С(z-z0)=0 (16), где А2+В2+С20
Прямая в пространстве.
Общие уравнения прямой в пространстве.
Т.к. линия в пространстве задается как линия пересечения 2-х поверхностей, то прямая в пространстве может быть задана как пересечение 2-х плоскостей:
A1x+B1y+C1z+D1=0 (1) – общее уравнение прямой
A2x+B2y+C2z+D2=0
Прямая задается либо 2-мя точками, либо точкой и направлением.
Канонические уравнения прямой.
Найдем уравнение прямой L, проходящей через точку М0(х0;у0;z0) параллельно вектору q=(l;m;n) - направляющий вектор прямой.
 Пусть
М(х;у;z) – переменная точка прямой. Тогда
вектор М0М=(x-x0)i+(y-y0)j+(z-z0)k
|| q=(l;m;n).
Пусть
М(х;у;z) – переменная точка прямой. Тогда
вектор М0М=(x-x0)i+(y-y0)j+(z-z0)k
|| q=(l;m;n).
Учитывая условие параллельности векторов получаем:
 (2) – каноническое уравнение прямой.
(2) – каноническое уравнение прямой.
В канонических
уравнениях (2) одно или два из чисел l,m
и n
могут быть равны нулю (все три не могут
равняться нулю, т.к. вектор q={l,m,n}
– ненулевой). Всякую пропорцию
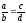 понимаем как равенствоad=cb.
Тогда обращение в нуль одного из
знаменателей в (2) означает обращение в
нуль и соответствующего числителя. Так,
например, если l=0,
то m0
и из равенства l(y-y0)=m(x-x0)
х-х0=0,
т.е. х=х1
– уравнение прямой, параллельной оси
Ох.)
понимаем как равенствоad=cb.
Тогда обращение в нуль одного из
знаменателей в (2) означает обращение в
нуль и соответствующего числителя. Так,
например, если l=0,
то m0
и из равенства l(y-y0)=m(x-x0)
х-х0=0,
т.е. х=х1
– уравнение прямой, параллельной оси
Ох.)
Если прямая задана своими общими уравнениями
A1x+B1y+C1z+D1=0 (1)
A2x+B2y+C2z+D2=0,
то направляющий вектор прямой q ортогонален каждому из нормальных векторов n1={A1;B1;C1}, n2={A2;B2;C2}. Так что можно положить вектор q={l,m,n} равный векторному произведению векторов n1 и n2:
q=n1×n2={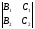 ;
-
;
-
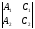 ;
;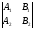 }={B1C2-B2C1;A2C1-A1C2;A1B2-A2B1}
}={B1C2-B2C1;A2C1-A1C2;A1B2-A2B1}
Чтобы из общих уравнений (1) получить канонические уравнения (2), необходимо кроме направляющего вектора q найти хотя бы одну точку М0(х0;у0;z0), через которую проходит прямая.
Пример.
Параметрические уравнения прямой.
Обозначим переменные для разного положения точки М, но равные друг другу отношения в уравнении (2) через t:
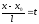
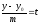

Преобразовав получаем параметрическое уравнение прямой:
 t
t R(3)
R(3)
Если
принять параметр t
за время, отсчитываемое от некоторого
начального момента, то параметрические
уравнения (3) определяют закон движения
материальной точки по прямой линии с
постоянной скоростью v= (такое движение происходит по инерции).
(такое движение происходит по инерции).
Уравнения прямой, проходящей через две заданные точки.
Даны
две точки на прямой М1(х1;у1;z1)
и М2(х2;у2;z2).
Т.к. точка М1 L,
то ее координаты удовлетворяют
каноническому уравнению этой прямой,
т.е.
L,
то ее координаты удовлетворяют
каноническому уравнению этой прямой,
т.е.
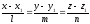
В качестве направляющего можно выбрать вектор
М1М2=(x2-x1)i+(y2-y1)j+(z2-z1)k
Тогда получаем уравнение прямой, проходящей через две заданные точки:
 (4)
(4)
Пример. Перевод из одного вида уравнения в другой.
Прямая проходит через точки А(2;-1;0) и В(0;2;1)
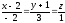 -
каноническое уравнение.
-
каноническое уравнение.
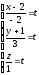
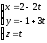 - параметрическое уравнение.
- параметрическое уравнение.
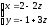
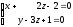 - общие уравнения.
- общие уравнения.
Взаимное расположение прямых в пространстве.
Для двух прямых в пространстве возможны 4 случая:
прямые совпадают;
прямые параллельны (но не совпадают);
прямые пересекаются;
прямые скрещиваются (т.е. не имеют общих точек и непараллельны).
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых.
 Пусть
прямые L1
и L2
заданы своими каноническими уравнениями
Пусть
прямые L1
и L2
заданы своими каноническими уравнениями
L1:
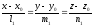 и L2:
и L2:

с направляющими векторами: q1=(l1;m1;n1) и q2=(l2;m2;n2).
Угол между прямыми L1 и L2 может быть определен как угол между векторами s1 и s2, т.е. (L1^L2)=(q1^q2). Тогда
сosφ= ,
т.е. сosφ=
,
т.е. сosφ=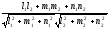 (4)
(4)
Условие параллельности прямых в пространстве.
L1||L2
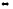 q1||q2
q1||q2
 (5)
(5)
Условие перпендикулярности прямых в пространстве.
L1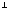 L2
L2
 q1
q1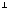 q2
q2
 q1·q2=0
q1·q2=0
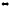 l1l2+m1m2+n1n2=0 (6)
l1l2+m1m2+n1n2=0 (6)
Выберем на прямых L1 и L2 точки М1(х1;у1;z1) и М2(х2;у2;z2) соответственно. Тогда канонические уравнения будут иметь вид:
L1:
 и L2:
и L2:
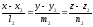
Если
прямые L1
и L2
совпадают,
то их направляющим векторам коллинеарен
и вектор М1М2,
т.е.
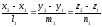 (7)
(7)
Это
двойное равенство означает, что точка
М2 L1.
Следовательно, условием совпадения
прямых является выполнения одновременно
равенств (5)
и (7).
L1.
Следовательно, условием совпадения
прямых является выполнения одновременно
равенств (5)
и (7).
Если прямые L1 и L2 пересекаются или скрещиваются, то их направляющие векторы неколлениарны, т.е. условие (5) нарушается.
