TUD_Nogin / TUD / intro

УДК 517.925

Ногин В.Д. Теория устойчивости движения. СПбГУ: ф-т ПМ-ПУ, 2008.

Систематически излагаются базовые понятия и методы теории устойчивости: изучены вопросы устойчивости и асимптотической устойчивости линейных дифференциальных систем, представлены результаты, лежащие в основе первого и второго методов Ляпунова.

Пособие предназначено для студентов второго курса факультета прикладной математики-процессов управления СПбГУ.

© В.Д. Ногин

Посвящается памяти Александра Михайловича Ляпунова Владимира Ивановича Зубова

Предисловие

Факультет прикладной математики-процессов управления (ПМ-ПУ) был создан на базе кафедры теории управления математико-механического факультета Ленинградского государственного университета в 1969 году. Заведовал этой кафедрой Владимир Иванович Зубов. Он же правительственным постановлением был назначен первым деканом факультета ПМ-ПУ. В настоящее время имя В.И. Зубова носит институт вычислительной математики и процессов управления СПбГУ.

Одно из основных направлений научной деятельности Владимира Ивановича было связано с теорией устойчивости. В рамках этого направления он активно развивал и применял на практике идеи и методы, разработанные на рубеже XIX и XX веков выдающимся русским математиком Александром Михайловичем Ляпуновым.

Со временем на факультете сформировалась крепкая научная школа в области теории устойчивости, а сама эта теория традиционно стала занимать важное место в списке изучаемых студентами фундаментальных дисциплин.

Предлагаемое учебное пособие предназначено для студентов второго курса. Освоение изложенного материала предполагает наличие у читателя определенных сведений и навыков из области теории дифференциальных уравнений, математического анализа и линейной алгебры.

Первая глава пособия посвящена изучению устойчивости наиболее простых – линейных дифференциальных систем. Во второй главе излагаются результаты, относящиеся ко второму методу Ляпунова, тогда как третья глава содержит основы первого метода Ляпунова.

Рисунки имеют двойную нумерацию в пределах главы, а теоремы, леммы, следствия, замечания и формулы нумеруются в пределах каждого параграфа.

Знак □ используется для указания начала, а ■ – конца доказательства. Большинство параграфов заканчиваются списком упражнений, выполнение которых будет способствовать закреплению изученного материала и развитию практических навыков у студентов.

Автор выражает искреннюю благодарность проф. А.Ю. Александрову за любезное согласие ознакомиться с рукописью данного пособия и за многочисленные ценные замечания по существу представленного в ней материала.

Следует добавить, что ответственность за все имеющиеся в тексте опечатки, погрешности и неточности несёт исключительно автор данного пособия. Смягчающим для него обстоятельством может служить лишь тот факт, что он не является специалистом в области теории устойчивости, но в силу сложившихся обстоятельств был вынужден разрабатывать и читать этот курс на факультете ПМ-ПУ.

Введение в теорию устойчивости

1о. Общее представление об устойчивости. Для того чтобы можно было поставить задачу об устойчивости, необходимо располагать

1)объектом, об устойчивости которого будет идти речь,

2)определением устойчивости.

Многие реальные динамические объекты могут быть описаны в терминах систем дифференциальных уравнений; в первую очередь – это различного рода механические системы. Именно поэтому в математической теории устойчивости исследуемым объектом является система обыкновенных дифференциальных уравнений. Что касается понятия устойчивости, то основным здесь является устойчивость по Ляпунову, в котором реализуется идея «малых» отклонений решения дифференциального уравнения на промежутке времени [0,+∞) при

«небольших» вариациях начальных данных этого решения.

Основная задача теории устойчивости состоит в разработке методов, которые позволяют судить об устойчивости заданного решения, не зная общего решения данной системы дифференциальных уравнений.

Эта теория была создана в конце XIX века великим русским ученым А.М. Ляпуновым. Совокупность всех методов теории устойчивости им была разделена на два класса. К первому классу он отнес те методы, которые при своем применении требуют определенную информацию о решениях исследуемой системы. Такой подход принято называть первым методом Ляпунова. Под вторым

методом Ляпунова понимают совокупность приемов и средств исследования устойчивости решений систем дифференциальных уравнений при помощи специальных функций Ляпунова.

Исследуемое на устойчивость частное решение принято называть невоз-

мущенным, тогда как любое другое – возмущенным решением.

Выделяют два типа устойчивости.

1) Устойчивость относительно возмущения начальных данных.

Смысл этого типа устойчивости состоит в том, что решения x = x(t; t0, x0) и x = x(t; t0, x1) с начальными данными (t0, x0) и (t0, x1) должны быть близкими для любого t ≥ t0, если x0 и x1 достаточно близки (рис.1).

Введение в теорию устойчивости_________________________________________________7

Рис.1. Близкие частные решения дифференциального уравнения.

Существенным здесь является требование близости решений при всех значениях t ≥ t0, так как если рассмотрение ограничить конечным интервалом изменения времени t, то указанное свойство сохранения близости будет прямым следствием классической теоремы о непрерывной зависимости решений системы дифференциальных уравнений от начальных данных.

2) Устойчивость относительно постоянно действующих внешних возмущений.

Если временной интервал конечен, то решения исходной x& = f(t, x) и возмущенной x& = f(t, x) + g(t, x) систем, выходящие из одной и той же начальной точки, будут близкими на данном конечном интервале, при условии, что внешние возмущения g(t, x) во второй системе достаточно малы. Это – прямое следствие классической теоремы о непрерывной зависимости решений системы дифференциальных уравнений от правых частей уравнений. Поэтому, когда говорят об устойчивости при постоянно действующих возмущениях, подразумевают, что t ≥ t0.

20. Примеры.

Пример 1 (Мальтус, 1802 г.). Рассмотрим модель эволюции популяции,

которая описывается линейным дифференциальным уравнением

где

x(t) – число особей в популяции в момент времени t, A – число особей, рождающихся в момент времени t, B – число особей, умирающих в момент времени t.

Общее решение уравнения (1) имеет вид

Введение в теорию устойчивости_________________________________________________8

Рис. 2. Кривые развития популяции при различных значениях k.

Здесь положение равновесия x ≡ 0 ведет себя следующим образом:

Рис. 3. Решения уравнения (1) в зависимости от значения параметра k.

Пример 2 (Ферхюльст, 1845 г.). Рассмотрим уточненную (логистическую) модель эволюции популяции Мальтуса при A = a·x, B = b·x2:

Введение в теорию устойчивости_________________________________________________9

x

x0 > a/b

x0 = a/b

x0 < a/b

t

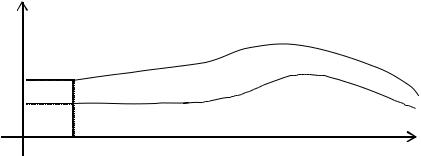
Рис. 3. Интегральные кривые в логистической модели (t0 = 0).

Здесь имеются два стационарных решения (положения равновесия): x ≡ 0 и x ≡ a/b,

так как a x – b x2 = b x ( x –a / b ) .

При наличии особей с течением времени в этой модели устанавливается стационарный режим x ≡ a/b, который устойчив: если популяция больше этого значения, то она со временем уменьшается, меньше – увеличивается.

Такая модель удовлетворительно описывает многочисленные явления насыщения, например, эволюцию популяции некоторых видов бактерий.

Если ее применять к оценке численности человечества, то следует иметь в виду, что сейчас население Земли составляет около 6 млрд., тогда как по оценкам экспертов стационарное значение этой величины есть a/b ≈ 16–20 млрд.

Логистическая модель и ее модификации успешно используются в экологии. Пусть, например, х – число рыб в озере или мировом океане. Выясним, как будет обстоять дело, если в модель добавить вылов рыбы с интенсивностью с:

Оказывается, результаты здесь сильно зависят от значения квоты вылова с. Для того чтобы установить это, сначала выполним преобразование правой части

Введение в теорию устойчивости_________________________________________________10

Предположим, что с < a2/4b. В этом случае квадратный трехчлен имеет два вещественных корня, которые обозначим через с1 и с2 , причем с1 ≤ с2.

x

c2

c1

t

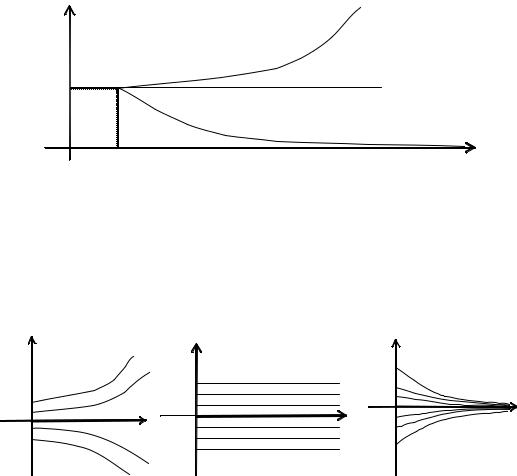
Рис. 4. Семейство интегральных кривых в модели Ферхюльста с квотой вылова.

Как видим из рис. 4, если начальное количество особей в популяции x0 = = x(t0) < с1, то всю рыбу обязательно выловят за некоторое конечное время.

Если же x0= с1 = с2 , то имеем неустойчивое состояние равновесия (рис.

6).

Оптимизация вылова обычно ведет к принятию «оптимального» значения с = a2/4b, поскольку человек заинтересован в увеличении квоты вылова с. Однако, как видно из рис. 6, такая политика может приводить (и в действительно-