
- •Пример 1. Рассмотрим стандартный полином
- •З а м е ч а н и е 1 (о распределении знаков полиномов h и g). Полиномы h и g имеют следующие знаки:
- •Упражнения
- •С помощью критерия Михайлова исследовать на устойчивость следующие уравнения:
- •§ 8. Теорема Харитонова
- •О п р е д е л е н и е 1. Интервальным полиномом называется множество полиномов вида
- •О п р е д е л е н и е 2. Интервальный полином называется полиномом Гурвица, если все полиномы, образующие его, являются полиномами Гурвица.
- •являлись полиномами Гурвица.
- •□ Необходимость очевидна.
- •Достаточность. Рассмотрим годограф Михайлова
- •для полинома
- •Введем полиномы
- •Тем самым,
- •Анализ доказательства теоремы 1 дает возможность сформулировать следующее утверждение.
- •Упражнения
- •§ 9. Лемма Гронуолла-Беллмана и ее обобщения
- •Результаты данного параграфа носят вспомогательный характер; они будет использованы далее.
- •Отсюда следует неравенство
- •которое можно переписать в виде
- •Тогда
- •□ Из (3) следует
- •Применяя лемму Гронуолла-Беллмана, получаем
- •Аналогично из (3) вытекает
- •Далее
- •где m > 1 и c – некоторая положительная константа.
- •Тогда имеет место неравенство
- •□ Из неравенства (5) следует
- •Отсюда с учётом (5) получаем
- •Интегрируя полученное неравенство, находим
- •а значит
- •где благодаря (6) выражение, записанное в квадратных скобках, строго положительно. Тогда
- •§ 10. Устойчивость линейных систем с переменной матрицей
- •Теорема 1. Пусть линейная система
- •□ Воспользуемся формулой Коши
- •Отсюда
- •Применяя лемму Гронуолла-Беллмана и используя условие (3), получаем
- •Пример 1. Рассмотрим уравнение
- •Оно эквивалентно системе
- •Характеристическое уравнение для матрицы соответствующей линейной системы имеет вид
- •устойчива. Далее,
- •а значит
- •Поэтому почти линейная система (*) также является устойчивой.
- •В теореме 1 речь шла об устойчивости линейной системы с почти постоянной матрицей. Вопрос об асимптотической устойчивости указанной системы решается в следующем утверждении.
- •Теорема 2. Если линейная однородная система
- •с постоянной матрицей А асимптотически устойчива, то таковой же будет и возмущенная линейная система
- •Запишем формулу Коши для системы (5):
- •Отсюда,
- •Но, как известно [2],
- •где с = с(ε) – некоторая положительная константа. Поэтому
- •Существует T > 0, для которого
- •С учетом полученного, из (**) следует
- •с постоянными матричными коэффициентами Аm,…,А0 асимптотически устойчива, если все корни характеристического уравнения det(λE – Am) = 0 имеют отрицательные вещественные части.
- •□ Полагая
- •исходную систему приводим к виду
- •З а м е ч а н и е 2. Для линейной системы с переменной матрицей А теорема 2, вообще говоря, неверна. Это подтверждает следующий пример.
- •Пример 2. Пусть
- •20. Неравенство Важевского. Это неравенство является полезным инструментом при исследовании устойчивости решений некоторых линейных однородных дифференциальных систем с переменной матрицей.
- •Теорема 3. Для всякого решения линейной системы
- •имеет место неравенство Важевского
- •Поэтому с учётом (*) получаем
- •то система (6) асимптотически устойчива.
- •Пример 3. Исследуем на асимптотическую устойчивость систему
- •Здесь
- •Отсюда
- •а значит
- •30. Необходимые условия устойчивости и асимптотической устойчивости. Обозначим через X(t) фундаментальную матрицу линейной системы (4) и выпишем известную из курса дифференциальных уравнений формулу Лиувилля
- •Непосредственно из этой формулы при помощи рассуждений от противного вытекают следующие два утверждения.
- •Теорема 5. Для асимптотической устойчивости линейной системы (6) необходимо, чтобы
- •З а м е ч а н и е 3. Примеры показывают, что необходимые условия теорем 4 и 5 не являются достаточными.
- •Пример 4. Рассмотрим линейную нестационарную систему
- •Согласно теореме 4 отсюда следует, что исходная система неустойчива.
- •Упражнения
- •1) Исследовать на асимптотическую устойчивость систему
- •2) Установить асимптотическую устойчивость системы
- •3) Установить асимптотическую устойчивость системы
- •4) Установить неустойчивость системы
ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ_______________________________________________58
степень |
ω |
со знаком |
+, |
из полученного следует, что |
ϕi (ω) |
монотонно |
||||||||||
возрастает от |
π |
до π. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
(ω) |
|
ϕk (ω) монотонно возрастают при изменении |
|||||||||
Итак, слагаемые ϕi |
и |
|||||||||||||||
ω от 0 |
до |
+ ∞, т. е. вектор |
f (iω) монотонно поворачивается против хода |
|||||||||||||
часовой стрелки на угол Φ = |
π n , выходя из точки |
f (0)= a0 > 0 и последова- |
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
тельно пересекая полуоси |
Imz >0, Rez < 0, |
Imz <0, Rez > 0,…, проходя по- |
||||||||||||||
очередно n квадрантов. |
|
|
|
|
|
|
|
|
|
|
f (iω) |
|||||
Теперь проверим обратное утверждение. Угол поворота вектора |
||||||||||||||||
при перемещении, указанном в формулировке теоремы, будет равен |
π |
n . Зна- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
чит, в соответствии с критерием Михайлова, f (z) – полином Гурвица ■ |
|
|
|
|||||||||||||
Пример 1. Рассмотрим стандартный полином |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
f(z) = z3 + 4z2 +9z +1. |
|
|
|
|
|
|
|
|||
Для него имеем |
f(iω) = (−4ω2 +1)+i ω(−ω2 +9). Находим точки пересе- |
|||||||||||||||
чения |
годографа |
с |
полуосями |
Rez > 0 , |
Imz > 0 |
и |
|
Rez < 0 : |
||||||||
ω1 = 0; |
ω2 = |
1 ; |
ω3 = 3. |
Далее, |
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
35 , |
|
|
|
|
|
|
|
|
|
|
f(i ω1 ) =1; |
f(i ω2 ) = i |
f(i ω3 ) = −35. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
Imz |
|
|
|
|
|
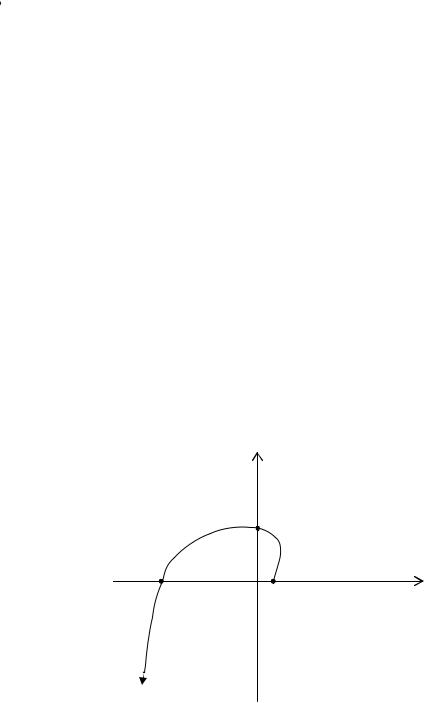
Следовательно, при воз- |
||||||
|
|
|
|
|
|
|
|
|
растании |
параметра |
ω |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
f(i ω2) |
|
|
|
|
|
|
от 0 |
до |
+ ∞ |
годограф, |
||||
|
|
|
|
|
|
|
|
|
|
выходя из точки |
|
(1, |
0) |
|||
|
|
|
|
|
|
|
|
|
|
положительной полуоси |
||||||
f(i ω3) |
|
|
|
f(i ω1) |
|
|
|
|
Rez > 0 , |
поворачивается |
||||||
–35 |
|
1 |
|
|
|
|
|
|
против часовой |
стрелки |
||||||
|
|
|
|
Rez |
|
|
и пересекает сначала по- |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
луось |
Imz > 0 , а затем |
– |
||||
|
|
|
|
|
|
|
|
|
|
Rez < 0 . |
Кроме |
того, |
||||
|
|
|
|
|
|
|
|
|
|
имеют место следующие |
||||||
|
|
|
|
|
|
|
|
|
|
предельные |
соотноше- |
|||||
|
|
|
|
|
|
|
|
|
|
ния |
−4ω2 +1 → −∞ |
и |
||||
|
Рис. 1.9. Расположение точек f(i ωk ) . |
|
ω −ω2(+9) → −∞ |
|
при |
|||||||||||
ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ_______________________________________________59
ω→ +∞, причём степень ω во втором выражении (мнимой части f(i ω) ) больше степени этого параметра в первом выражении (вещественной части f(i ω) ). В соответствии с теоремой 2 f(z) = z3 +4z2 +9z +1 является полино-
мом Гурвица.
Продолжим получение необходимых и достаточных условий того, что стандартный полином f(z) = a0 +a1z +... +a n zn является полиномом Гурвица. С этой целью введём вещественную g и мнимую h части f(iω) :
f(iω) = g(ω) +i h(ω) ,
g(ω) = a0 − a2ω2 + a 4ω4 − a6ω6 +K,
h(ω) = a ω− a |
3 |
ω3 + a |
5 |
ω5 − a |
7 |
ω7 +K, |
||
1 |
|
|
|
|
|
|||
где вид и знак последнего слагаемого в |
g( ω) |
и |
h( ω) зависит от четности и |
|||||
степени полинома f(z) . Заметим, что g – чётная, а h – нечётная функции. |
||||||||
Теорема 3. Для того чтобы стандартный полином f(z) степени n был |
||||||||
полиномом Гурвица, необходимо и достаточно, |
чтобы полиномы g( ω) и |
|||||||
h( ω) в сумме имели n неотрицательных корней, которые не совпадают друг с другом и перемежаются, т. е.
0 = ω1 < ω2 <K< ωn ,
g(ω2k ) = 0, h(ω2k-1) = 0, |
k =1,2,3,K |
и, кроме того, a1 > 0 .
□ Необходимость. Так как f(z) – полином Гурвица, то у него все коэффи-
циенты положительны и он не имеет чисто мнимых корней. По теореме 2 существуют такие неотрицательные числа ω1 , ω2 ,..., ωn , что
Im f(i ω1 ) = h(ω1 ) = 0; |
Re f(i ω2 ) = g(ω2 ) = 0; |
|
Im f(i ω3 ) = h(ω3 ) = 0; |
Re f(i ω4 ) = g(ω4 ) = 0; |
(*) |
Im f(i ω5 ) = h(ω5 ) = 0;K |
|
|
причем 0 = ω1 < ω2 <K< ωn .
Последнее равенство в цепочке (*) зависит от чётности степени полинома f(z) . Так, если n = 2k +1, то h( ωn ) = 0 , а если n = 2k , то g( ωn ) = 0 .
Поскольку вещественная часть g(ω) годографа Михайлова является
чётной функцией, а мнимая часть – нечётной, то полиномы g и h имеют в сумме не более n неотрицательных корней.

ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ_______________________________________________60
Из (*) следует, что полиномы g и h имеют в сумме ровно |
n |
|
неотрица- |
|||||||||||
тельных корней, которые не совпадают друг с другом и перемежаются. |
|
|
|
|||||||||||
Действительно, если |
n – нечётное, то n – 1 – чётное. В этом случае по- |
|||||||||||||
лином g имеет не более |
n – 1 |
различных корней и среди них не более |
n −1 |
|||||||||||
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
n +1 |
|
||||
различных неотрицательных корней, тогда как h имеет не более |
|
|
раз- |
|||||||||||
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
личных неотрицательных корней. В сумме получаем не более |
|
n −1 |
+ |
n +1 |
= n |
|||||||||
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
неотрицательных корней. Если же |
n – чётное, то n – 1 – нечётное, а значит g, |
|||||||||||||
равно как и h, имеет не более |
n |
неотрицательных корней. Поэтому в итоге |
||||||||||||
вновь получаем не более n |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
различных неотрицательных корней. |
|
|
|
|
|
|
|
|
|
|||||
С другой стороны, согласно (*), рассматриваемые полиномы в сумме об- |
||||||||||||||
ладают не менее n различными неотрицательными корнями |
ω1,ω2 ,K,ωn . |
|||||||||||||
Следовательно, полиномы g и h |
имеют в сумме ровно n неотрицательных |
|||||||||||||
корней. |
|
|
годограф Михайлова f( iω) |
|
|
|
|
|
|
|
|
|
f(z) , |
|
Достаточность. По условию, |
полинома |
|
||||||||||||
не обращаясь в нуль, монотонно поворачивается против хода часовой стрелки (так как h( ω1 ) = 0, g( ω1 ) = a0 > 0, g( ω2 ) = 0,K и a1 > 0 ), последовательно
пересекая полуоси Re z > 0 , Im z > 0 , Re z < 0 , Im z < 0 , …, проходя n квадран-
тов. Значит Φ = π2 n . Согласно теореме 2 отсюда следует, что f(z) – полином
Гурвица ■
З а м е ч а н и е 1 (о распределении знаков полиномов h и g). Полиномы h и g имеют следующие знаки:
h( ω) > 0 |
ω (ω1,ω3 ); |
g( ω) > 0 |
ω (ω1,ω2 ); |
h( ω) < 0 |
ω (ω3,ω5 ); |
g( ω) < 0 |
ω (ω2 ,ω4 ); |
h( ω) > 0 |
ω (ω5,ω7 ); |
g( ω) > 0 |
ω (ω4 ,ω6 );K |
Упражнения
С помощью критерия Михайлова исследовать на устойчивость следующие уравнения:
1)x(4) + x(3) +5x& +16x = 0 ,
2)2x(4) +11x(3) + 21&x&+ 25x& + 7x = 0 ,

ГЛАВА 1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ_______________________________________________61
3)x(5) + x(4) + 2x(3) +3&x&+ 4x& +5x = 0 ,
4)x(3) + 3&x&+ 4x& +17x = 0 .
§ 8. Теорема Харитонова
При формировании системы дифференциальных уравнений, моделирующей те или иные реальные процессы, неизбежно возникают погрешности и ошибки, которые приводят к тому, что участвующие в математической модели параметры и коэффициенты не могут быть определены точно. Чаще всего удается указать лишь интервал, которому должен принадлежать тот или иной коэффициент. В случае, если в роли указанной математической модели выступает линейная однородная система дифференциальных уравнений с постоянными коэффициентами, то отмеченная неточность будет проявляться и в коэффициентах характеристического полинома, расположение корней которого на комплексной плоскости, как мы знаем, существенным образом влияет на устойчивость и асимптотическую устойчивость системы. В этой связи важным с практической точки зрения является вопрос получения необходимых и достаточных условий того, чтобы полиномами Гурвица были все полиномы, коэффициенты которых расположены в некоторых интервалах. Такого рода условия излагаются ниже.
О п р е д е л е н и е 1. Интервальным полиномом называется множество полиномов вида
{a |
0 |
+a z +a |
2 |
z2 |
+K+a |
zn−1 +a |
n |
zn}, |
(1) |
|
|
1 |
|
|
n-1 |
|
|
|
|||
где ai ≤ ai ≤ ai и ai ,ai – фиксированные числа, |
i = 0,K,n . |
|
||||||||
О п р е д е л е н и е 2. Интервальный полином называется полиномом Гурвица, если все полиномы, образующие его, являются полиномами Гурвица.
Теорема 1 (В.Л. Харитонов1). Для того чтобы интервальный полином (1) был полиномом Гурвица, необходимо и достаточно, чтобы следующие четыре “угловых” полинома
f1( z) = a0 +a1z +a2z2 + a3z3 + a4z4 +K,
f2 ( z) = a0 + a1z + a2z2 +a3z3 +a4z4 +K,
f3( z) = a0 + a1z +a2z2 +a3z3 + a4z4 +K,
f4 ( z) = a0 +a1z + a2z2 + a3z3 +a4z4 +K,
1 Ученик В.И. Зубова, В.Л. Харитонов является профессором кафедры теории управления факультета ПМ-ПУ.
