

ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА
Под первым методом Ляпунова понимают совокупность приемов и средств исследования устойчивости решений систем дифференциальных уравнений, основанных непосредственно на анализе общих или частных решений этих систем, а также использующих определенные характеристики указанных решений.
§ 1. Характеристический показатель функции
10. Определение характеристического показателя функции. Рассмот-
рим комплекснозначную функцию
f(t) = f1(t) + i f2(t) |
t ≥ 0, |
где f1 и f2 – некоторые вещественные функции. Имеет место представление
f(t) = eα(t) t ,
где
α(t) = 1t ln f (t).
Из данного представления видно, что, исследуя величину α(t), можно изучать скорость роста функции |f (t)| по сравнению со скоростью роста экспоненты.
О п р е д е л е н и е 1. Число (или один из символов – ∞, + ∞), определяемое равенством
χ[f ]= |
___ |
1 |
ln | f(t) |, |
lim |
|||
|
t→+∞ t |
|
|
называют показателем Ляпунова (характеристическим показателем).
З а м е ч а н и е 1. Для обеспечения корректности в приведенном определении предполагается, что существует последовательность tk → +∞ при k → +∞, такая, что |f(tk)| ≠ 0 для всех натуральных k, начиная с некоторого номера.
З а м е ч а н и е 2. Отметим следующий факт, вытекающий из определе-
ния верхнего предела: |
для любой |
последовательности {tk}, такой что |
||||
tk → +∞, выполнено неравенство |
|
|
|
|||
___ |
1 |
|
|
___ |
|
|
lim |
ln | f(tk ) | ≤ |
χ[f ]= |
lim 1 |
ln | f(t) |. |
||
|
||||||
k→+∞ tk |
|
t→+∞ t |
|
|||
ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________116
|
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1) |
Пусть |
f(t) = eαt , |
α R . Тогда |
χ[eαt ] = α |
и в случае α > 0 выполнено |
|||||||||||||||||||||
f(t) → +∞, а при α < 0 верно |
f(t) → 0 |
( t → +∞). |
|
|
|
|
||||||||||||||||||||
2) χ[t |
m |
] = |
___ |
|
|
1 |
ln t |
m |
= 0 , |
m R . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
t→+∞ t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
χ[e |
t sint |
|
___ |
|
1 |
| t sint |=1. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
] = lim |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
t→+∞ t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4) χ[et2 ] = |
___ |
|
|
1 |
ln et2 |
= +∞. |
|
|
|
|
|
|
|
|
|
|
||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
t→+∞ t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
20. Свойства характеристических показателей. |
|
|
|
|
|||||||||||||||||||||
1) |
χ[f(t)] = χ[| f(t) |]. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2) |
χ[c f(t)] = χ[f(t)] |
c ≠ 0 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3) | f(t) |≤| F(t) | |
|
t > T |
|
χ[f(t)] ≤ χ[F(t)]. |
|
|
|
|
||||||||||||||||||
|
□ Это свойство вытекает из определения характеристического показателя |
|||||||||||||||||||||||||
|
и свойства монотонности верхнего предела: |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ϕ(t) ≤ ψ(t) |
t > T |
|
___ |
___ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
lim ϕ(t) ≤ |
lim ψ(t) ■ |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t→+∞ |
t→+∞ |
|
|
|
|
4) |
Пусть χ[f(t)] = α ≠ ±∞. Тогда для любого |
ε > 0 выполнено |
|
|
|
|||||||||||||||||||||
|
|
|
i) |
lim |
|
|
| f(t) | |
|
= 0; |
|
|
|
|
|
|
|
|
|
|
(1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
t |
→+∞ e(α+ε) t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
___ |
|
|
| f(t) | |
|
= +∞; |
это означает существование такой последова- |
||||||||||||||
|
|
|
ii) |
|
lim |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
t→+∞ e(α−ε) t |
|
|
|
|
|
что |
|
|
|
|
|
|
|
||||||||
|
|
|
тельности {tk}, tk → +∞, |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
| f(tk ) | |
|
= +∞. |
|
|
|
(2) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k→+∞ e |
(α−ε) t k |
|
|
|
|
|
|
|
||
|
|
|
|
|
Обратно, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
если |
найдется |
|
такое |
α R , |
что |
|
для |
всякого |
ε > 0 |
верно |
(1), |
то |
|||||||||||||
|
χ[f ] ≤ α; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
если |
найдется |
|
такое |
α R , что |
|
для |
всякого |
ε > 0 |
верно |
(2), |
то |
||||||||||||||
|
χ[f ] ≥ α; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
если найдется такое |
α R , что для всякого ε > 0 выполнено (1) – (2), |
||||||||||||||||||||||||
|
то χ[f ] = α. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
□ Необходимость. Выберем произвольное ε > 0 и пусть

ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________117
|
χ[f ]= |
___ |
1 ln | f(t) |= α R . |
||||
|
lim |
||||||
|
|
t→+∞ t |
|
||||
По определению верхнего предела найдется такое T, что |
|||||||
1 |
ln | f(t) |< |
α + |
ε |
|
t > T |
||
t |
|
||||||
|
|
|
2 |
|
|
||
и |
|
1 |
|
|
|
|
|
|
lim |
ln | f(tk ) |= α |
|
||||
|
|
|
|||||
|
t→+∞ |
tk |
|
|
|
|
|
для некоторой последовательности tk → +∞ при k → +∞. Следовательно, при некотором натуральном N справедливо
|
|
|
|
|
|
|
|
ε |
|
t > T , |
|
|
|
|
|
|
| f(t) |< e(α+ε2 ) t = e(α+ε) t e−2 t |
|
|
||||||
|
|
|
|
| f(tk ) |> e(α−ε2 ) tk |
= e(α−ε) tk |
e2ε tk |
|
k > N , |
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
ε |
t |
|
|
|
|
|
ε |
tk |
|
|
e |
|
→ 0 ( t → +∞) |
и |
e2 |
→ +∞ ( k |
→ +∞). |
||||||
2 |
|
|
||||||||||
Отсюда вытекают равенства (1) – (2). |
|
|
|
|
|
|||||||
Достаточность. Из (1) следует |
|
|
|
|
|
|||||||
|
|
|
|
χ[f ] ≤ χ[e(α+ε) t ] = α+ε |
|
ε > 0 , |
|
|||||
а значит χ[f ] ≤ α. С другой стороны, из (2) имеем |
|
|||||||||||
|
|
|
|
___ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
χ[f ] ≥ lim |
|
|
ln | f(tk ) |≥ α −ε ε > 0 , |
|
||||
|
|
|
|
|
|
|||||||
|
|
|
|
k→+∞ tk |
|
|
|
|
|
|
||
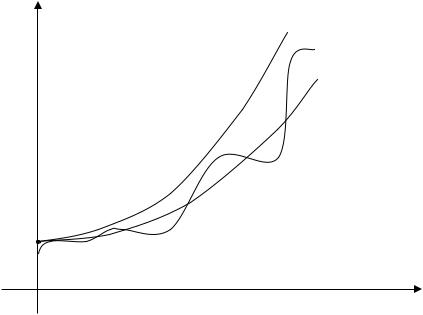
и поэтому χ[f ] ≥ α. Полученные неравенства влекут равенство χ[f ] = α ■ Пусть для определенности χ[f ] = α > 0 (случай α < 0 разбирается аналогично). Величина характеристического показателя дает возможность сравнить скорости роста данной функции (точнее говоря, ее модуля) и экспоненты. А именно, в соответствии с доказанным свойством
функция модуля y =| f(t) | |
для любого ε > 0 растет медленнее, чем экс- |
||
понента y = e(α+ε) t , но по некоторой последовательности t |
k |
→ +∞ бы- |
|
1 |
|
|
|
стрее, чем экспонента y2 |
= e(α−ε) t (см. рис. 3.1). |
|
|
ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________118
y
y1=e(α+ε) t y=|f(t)|
y2=e(α–ε) t
1
t
0
Рис. 3.1. Характеризация скорости роста функции y = |f(t)|.
5) Пусть χ[fk ] R, k =1,2,...,m . Характеристический показатель суммы конечного числа функций f1(t),...,fm (t) не превышает наибольшего из ха-
рактеристических показателей этих функций и совпадает с ним, если наибольшим характеристическим показателем обладает лишь одно этих из слагаемых:
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
χ[∑fk ] ≤ max χ[fk ]. |
|
(3) |
||||||||
|
|
|
|
|
k=1 |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
□ Пусть α:= max χ[fk ] ≠ ±∞. Согласно предыдущему свойству |
(часть |
||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
«необходимость») для любого ε > 0 |
|
имеем |
|
|
|||||||||
|
|
lim |
| fk (t) | |
= 0, |
|
k =1,2,...,m . |
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
t→+∞ e(α+ε) t |
|
|
|
|
|
|
|
|
|||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
0 ≤ |
|
| ∑fk (t) | |
m |
|
| f |
k |
(t) | |
= o(1) |
( t → +∞). |
|
|||
|
k=1 |
|
|
≤ |
|
|
|||||||
|
e( +ε) t α |
|
|
|
|
|
|
||||||
|
|
k∑=1 e( |
|
+ε) t α |
|
|
|||||||
Согласно предыдущему свойству (часть «достаточность»), верно
ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________119
m |
|
|
χ[∑fk ] ≤ α = max χ[fk ]. |
(*) |
|
k=1 |
k |
|
|
|
|
Тем самым, неравенство (3) установлено. |
|
|
Теперь пусть max χ[fk ] = χ[fp ] = α, причем χ[fk ] = αk < α для всех |
k ≠ p . |
|
k |
|
|
В соответствии с частью «необходимость» предыдущего свойства для любо-
го ε > 0 существует последовательность |
|
{tq}: tq → +∞ при q → +∞, при- |
||||||||||||||||||||||
чем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
| fp (tq ) | |
= +∞. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
q→+∞ e |
(α−ε) tq |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если 0 < ε < min α −αk , то при |
αk ≠ −∞ |
|
справедливо неравенство |
|||||||||||||||||||||
k≠p |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ∑fk (tq ) | |
|
| fp (tq ) | |
− ∑ |
| fk (tq ) | |
|
|
1 |
|
|
||||||||||||||
|
k=1 |
|
|
≥ |
|
|
|
|
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
e |
( |
−ε) t |
α |
|
e |
( −ε) t |
α |
|
(α |
+ε) t |
|
|
e |
(α−α |
−2ε)t |
|
|||||||
|
|
q |
|
|
|
|
|
q |
|
k≠p e |
|
k |
|
q |
|
k |
|
q |
||||||
|
|
|
|
|
|
14243 |
|
14444244443 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
→+∞ |
|
|
|
|
|
|
→0 |
|
|
|
|
|||||
где q → +∞. Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ∑fk (tq ) | |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
lim |
k=1 |
|
|
|
= +∞, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
q→+∞ |
|
e |
(α−ε) tq |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а значит, в соответствии с частью «достаточность» предыдущего свойства, получаем неравенство
m
χ[∑fk ] ≥ α.
k=1
Это вместе с неравенством (*) ведёт к требуемому равенству
m |
|
χ[∑fk ] = α = max χ[fk ] ■ |
|
k=1 |
k |
|
|
6)Пусть χ[fk ] R, k =1,2,...,m . Характеристический показатель произведения конечного числа функций f1(t),...,fm (t) не превышает суммы характеристических показателей этих функций, т.е.

ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________120
m m
χ[∏fk ] ≤ ∑χ[fk ].
k=1 k=1
□ Используя свойство верхнего предела, легко получаем требуемое
m |
___ |
1 |
m |
___ |
1 |
m |
|
|
χ[∏fk (t)] = |
lim |
ln | ∏fk (t) |= |
lim |
∑ln | fk (t) | ≤ |
|
|||
k=1 |
t→+∞ t |
k=1 |
t→+∞ t |
k=1 |
■ |
|||
|
|
|
|
m |
___ |
1 |
m |
|
|
|
|
|
|
||||
|
|
|
≤ ∑ lim |
ln | fk (t) | = ∑χ[fk (t)] |
|
|||
|
|
|
|
k=1 t→+∞ t |
k=1 |
|
||
Следствие 1. Характеристический показатель конечной линейной комбинации функций f1(t),...,fm (t) с ограниченными коэффициентами
c1(t),...,cm (t) не превышает наибольшего из характеристических показателей данных функций:
m |
|
χ[∑ck (t) fk (t)] ≤ max χ[fk (t)] . |
|
k=1 |
k |
|
|
□ В самом деле, с учётом χ[ck (t)] ≤ 0 имеем |
|
m |
|
|
χ[∑ck (t) fk (t)]≤ max χ[ck (t) fk (t)]≤ max{χ[ck (t)] + χ[fk (t)]}≤ |
||
k=1 |
k |
k |
Если ck(t) ≡ ck, то получаем следующий результат.
m
Следствие 2. Пусть в линейной комбинации ∑ck fk (t)
k=1
max χ[fk (t)] ■
k
с отличными от
нуля постоянными коэффициентами есть единственная функция с наибольшим характеристическим показателем. Тогда
m |
|
χ[∑ck fk (t)] = max χ[fk (t)] . |
|
k=1 |
k |
|
|
|
Упражнения |
1)Вычислить характеристические показатели следующих функций:
(i)y = t e2t
(ii)y = t100 e0.1 t
(iii)y = (1+ee−t ) sin t

ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________121
(iv) y = ln(1 + 2t ) .  t
t
2)Существуют ли ограниченные на промежутке [0,+∞) функции, имеющие бесконечные характеристические показатели + ∞ или − ∞?
§2. Характеристический показатель функциональной матрицы
Введенное в предыдущем параграфе понятие характеристического показателя функции здесь распространяется на векторные функции, а также функциональные матрицы. При этом основные из установленных ранее свойств сохраняются.
10. Определение.
О п р е д е л е н и е 1. Пусть F(t) = (f jk (t)) – матрица, определенная на [0,+∞) . Число (или один из символов + ∞, −∞) определяемое равенством
χ[F(t)] = max χ[f jk (t)] ,
j,k
называется характеристическим показателем матрицы F(t) .
Очевидно, χ[FT (t)] = χ[F(t)] .
20. Свойства характеристических показателей матриц.
1) Характеристический показатель матрицы |
F(t) = (f jk (t)) совпадает с |
|||||
характеристическим показателем ее нормы1, т.е. |
|
|||||
|
|
χ[F(t)] = χ[|| F(t) ||]. |
|
(1) |
||
□ Для любого |
t ≥ 0 и всех |
j,k |
верно неравенство |
| f jk (t) |≤|| F(t) ||, от- |
||
куда следует |
χ[f jk (t)] ≤ χ[|| F(t) ||], а значит |
|
|
|||
|
|
χ[F(t)] ≤ χ[|| F(t) ||]. |
|
(*) |
||
С |
другой стороны, |
для |
всех |
t ≥ 0 |
можно записать |
|
|| F(t) ||≤ |
∑| f jk (t) |. Следовательно, согласно свойству 5) характеристиче- |
|||||
|
j,k |
|
|
|
|
|
ских показателей, получаем |
|
|
|
|
||
|
|
χ[|| F(t) ||] ≤ max χ[f jk ] = χ[F(t)] . |
(**) |
|||
|
|
|
j,k |
|
|
|
1 Определение нормы матрицы (три варианта) см. в § 3 гл. 1.
ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________122
Из неравенств (*) – (**) вытекает равенство (1) ■
2)Пусть χ[Fs ] R, s =1,2,..., N . Характеристический показатель суммы конечного числа матриц Fs не превышает наибольшего из характери-
стических показателей этих матриц. |
|
|
□ Пусть Fs (t) ( s =1,2,..., N) – матрицы размера |
m ×n и |
|
|
N |
|
|
F(t) := ∑Fs (t) . |
|
|
s=1 |
|
|
N |
|
Для всех t ≥ 0 верно || F(t) ||≤ ∑|| Fs (t) ||. |
Поэтому |
|
|
s=1 |
|
N |
|
|
χ[F(t)] = χ[|| F(t) ||] ≤ χ[∑||Fs (t) ||] ≤ max χ[|| Fs (t) ||] = max χ[Fs (t)] ■ |
||
s=1 |
s |
s |
|
|
|
Следствие 1. Если среди матриц Fs (t) ( s =1,2,..., N) имеется лишь |
||
одна, обладающая наибольшим характеристическим показателем, то характеристический показатель суммы данных матриц равен этому наибольшему характеристическому показателю.
|
□ В самом деле, пусть |
χ[F1(t)] > χ[|| Fs (t) ||] для всех s >1, |
||||
F |
(t) = |
(f (s) (t)) , s = 1,2,...,N, |
и |
|
|
|
s |
|
jk |
|
|
|
|
|
|
|
|
N |
|
|
|
|
F(t) := ∑Fs (t) = (f jk (t)) . |
||||
|
|
|
|
s=1 |
|
|
Кроме того, пусть χ[F (t)] = max χ[f (1) (t)] = χ[f (1) |
(t)]. Поскольку |
|||||
|
|
1 |
j,k |
jk |
pq |
|
|
|
|
|
|
|
|
|
|
χ[f (s) (t)] ≤ χ[F (t)] < χ[f (1) |
(t)] |
s >1, |
||
|
|
pq |
s |
pq |
|
|
с использованием свойства 5) характеристических показателей получаем
χ[fpq (t)] = χ[fpq(1) (t)] = χ[F1(t)].
Следовательно,
χ[F(t)] ≥ χ[F1(t)] = max χ[Fs (t)].
s
Отсюда, в силу доказанного выше свойства 2), следует
χ[F(t)] = max χ[Fs (t)] ■
s

ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________123
3)Пусть χ[Fs ] R, s =1,2,..., N . Характеристический показатель произведения конечного числа матриц Fs не превышает суммы характеристи-
ческих показателей этих матриц.
N
□ Пусть F(t) := ∏Fs (t) . Норма произведения матриц не превышает про-
s=1
N
изведения норм этих матриц: || F(t) ||≤ ∏|| Fs (t) ||. Поэтому с использова-
s=1
нием свойства 6) характеристических показателей, получаем
N |
N |
χ[F(t)] = χ[|| F(t) ||]≤ ∑χ[|| Fs (t) ||] = ∑χ[Fs (t)] ■ |
|
s=1 |
s=1 |
Следствие 2. Характеристический показатель линейной комбинации
N
∑cs Fs (t) (cs ≠ 0, s =1,2,..., N) нескольких матриц с постоянными ко-
s=1
эффициентами не превышает наибольшего из характеристических этих матриц и равен ему, если наибольшим характеристическим показателем обладает лишь одна из данных матриц.
Упражнение
1. Вычислить характеристический показатель матрицы
|
t2 +t+1 |
− 1−t+t2 |
e |
t2 |
+t |
−t |
|
|
||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
F(t) = |
|
|
|
|
|
|
|
|
|
ln(1+3 |
|
. |
ln(1+2t ) |
1 |
+3 |
t |
(1+ |
2 |
t |
) |
t |
) |
|||
|
|
|
|
|
|
|||||||
§ 3. Спектр линейной однородной системы
Рассмотрим линейную дифференциальную систему |
|
||
|
dx |
= A(t) x , |
(1) |
|
|
||
|
dt |
|
|
матрица которой составлена из непрерывных на промежутке |
[0,+∞) и в общем |
||
случае комплекснозначных функций.
Теорема 1. Если матрица A(t) линейной системы (1) ограничена на
[0,+∞) , т.е. существует такое число c, что

ГЛАВА 3. ПЕРВЫЙ МЕТОД ЛЯПУНОВА_______________________________________________________124
|
A(t) |
|
|
|
≤ c < +∞ |
t ≥ 0 , |
|
|
|
то каждое вещественное или комплексное ненулевое решение x = x(t) системы (1) имеет конечный характеристический показатель.
□ Пусть x(t) = (x1 (t),..., xn (t))T – произвольное ненулевое решение системы (1), t ≥ 0 . Заметим, что 
 x(0)
x(0)
 ≠ 0 , так как в противном случае благодаря единственности решения с начальными данными (0, x(0)) оно должно было
≠ 0 , так как в противном случае благодаря единственности решения с начальными данными (0, x(0)) оно должно было
быть нулевым.
Из (1) вытекает
t |
|
x(t) = x(0) + ∫A(τ) x(τ)dτ. |
|
0 |
|
Следовательно, |
|
t |
|
|| x(t) ||≤|| x(0) || + | ∫|| A(τ)|| || x(τ)|| dτ| |
t ≥ 0 . |
0 |
|
Применяя обобщенную лемму Гронуолла-Беллмана (см. § 9 гл. 1), при t ≥ 0 получим
|
t |
|
t |
|
|
|
|
|
|
|
|
|| x(0) || exp |
− ∫|| A(τ)||dτ |
≤|| x(t) ||≤|| x(0) || exp |
∫|| A(τ)||dτ . |
||
|
0 |
|
|
0 |
|
Предварительно разделив эти неравенства на положительное число 
 x(0)
x(0)
 , с учетом равенства
, с учетом равенства
x(t)
χ= χ[x(t)]
 x(0)
x(0)

находим
|
|
− |
t |
|
|
t |
|
|
χ exp |
∫ |
|| A(τ)||dτ |
≤ χ[x(t)] ≤ χ exp |
∫ |
|| A(τ)||dτ . |
|||
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
0 |
|
Отсюда
− A ≤ χ[x(t)] ≤ A ,
где
