0491803_E70E2_voprosy_k_ekzamenu_po_statistike / 24_slu4_sredn_pred_owibki

Вопрос 24. Собственно-случайная, средняя и предельная ошибки выборки.

Коэффициент доверия.

Выборочным называется такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.

Средняя и предельная ошибки выборки

Средняя ошибка выборки всегда присутствует в выборочных исследованиях и появляется вследствие того, что обследуются не все единицы статистической совокупности, а лишь ее часть.

Средняя ошибка выборки превращается в предельную ошибку Δ при умножении ее на коэффициент доверия t, который задается предварительно, исходя из требуемой точности наблюдения. Предельная ошибка позволяет судить об «истинном» размере параметра в генеральной совокупности с определенной степенью вероятности

, -предельная ошибка , -средняя ошибка, t – коэффициент доверия

При типическом и серийном отборе, при расчете ошибки выборки вместо общей дисперсии (σ²) следует использовать среднюю из внутригрупповых дисперсий и межгрупповую дисперсию, где - частная дисперсия i группы, объем i группы

Формулы предельной ошибки случайной выборки при определении средней

Для повторного отбора

где средняя ошибка выборки

Для бесповторного отбора

Формулы предельной ошибки случайной выборки при определении доли

Для повторного отбора

где средняя ошибка выборочной доли

Для бесповторного отбора

где средняя ошибка выборочной доли

Формулы численности случайной выборки при определении средней величины

Для повторного отбора	Для бесповторного отбора

Формулы численности случайной выборки при определении доли изучаемого признака

Для повторного отбора	Для бесповторного отбора

Предельная разница между генеральной и выборочной средней соответствует величине предельной ошибки

для средней	для доли:

Значения вероятности и соответственно t находятся по таблицам распределения:

• Лапласа

• Стьюдента (в случае малой выборки)

Формулы случайной выборки подходят и для механической выборки.

При необходимости округления, при случайной выборке – округление в большую сторону, при механической – в меньшую.

Малая выборка

Если численность выборочной совокупности не более 30 единиц, то средняя ошибка малой выборки при определении средней величины рассчитывается по формуле:

	при определении доли по формуле:

Для расчета ошибки малой выборки применяется уточненная формула дисперсии

где n-1 - представляет собой «число степеней свободы», т.е. количество вариантов, могущих принимать произвольные значения, не меняющие величины средней.

Типы задач выборочного наблюдения

• определение ошибки выборки,

• определение численности выборочной совокупности n ,

• определение вероятности того, что выборочная средняя (или доля) отклонится от генеральной не более, чем на заданную величину t=Δ/μ,

• оценка случайности расхождений показателей выборочных наблюдений,

• перенос выборочных характеристик на генеральную совокупность.

Проверка гипотез о средней и доле

Оценка случайности расхождений показателей выборочных наблюдений

• Если при n>30 коэффициент t<3, то делается вывод о случайности расхождений.

• Если n ≤ 30 , то полученное значение t сравнивают с табличным, определяемым по таблице распределения Стьюдента

• Если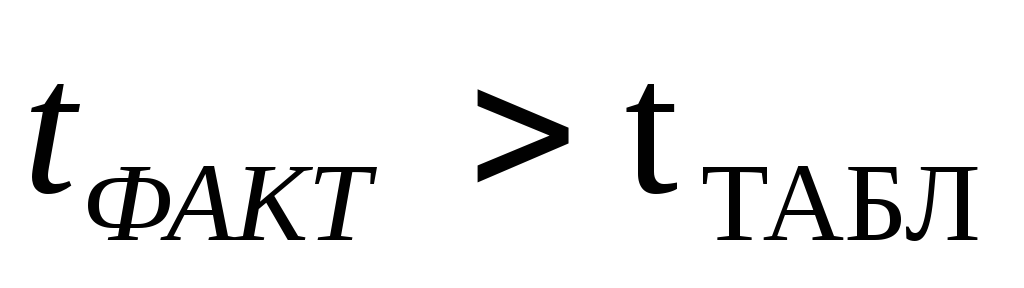, расхождение считается существенным.

• Если 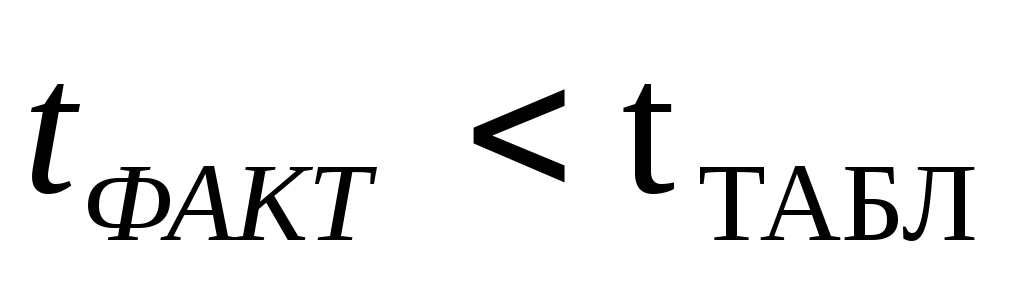, расхождение считается случайным.

Методы переноса выборочных данных на генеральную совокупность

• метод взвешивания;

• метод перевзвешивания;

• метод заполнения случайным подбором в классах замещения.