2. Непрерывные функции. Теорема Больцано-Коши о промежуточном значении функции. Теорема Вейерштрасса о наибольшем и наименьшем значении функции.

Определение 1. Функция называется непрерывной в точке , если

или, что то же,

Определение 2. Функция называется непрерывной на множестве , если она непрерывна в каждой его точке.

Замечание 1. В следующей теореме используется принцип Кантора вложенных отрезков: для всякой системы вложенных отрезков (таких, что для каждой пары один содержится в другом) существует общая точка. А если отрезки стягиваются, то такая точка -- единственная.

Теорема 1. (Больцано--Коши) если непрерывна на и на концах принимает значения разных знаков ( ), то существует точка такая, что .

Доказательство. Для определенности пусть , а . Рассмотрим точку как середину отрезка . Если , то теорема доказана. Если это не так, будем рассматривать тот из двух получившихся отрезков, значения функции на концах которого разных знаков. Поступая аналогично, либо закончим процесс деления на некотором шаге, либо получим стягивающуюся систему вложенных отрезков . Тогда, согласно принципу Кантора, существует единственная общая точка . Покажем, что . Заметим, что , , , . Поскольку , то функция непрерывна в этой точке, следовательно, и . Тогда .

Теорема Вейерштрасса о достижении непрерывной функцией своего наибольшего и наименьшего значений: если функция f(x) непрерывна на [a,b], то найдется такая точка , в которой функция достигает своего максимума, найдется такая точка , в которой функция достигает своего минимума.

Доказательство:

Пусть функция f(x) непрерывна на [a,b], тогда в силу теоремы 1 она ограничена на этом отрезке. Следовательно, ограничено множество значений функции. Тогда в силу принципа верхней грани это множество обладает точной верхней и точной нижней границами.

Обозначим: и покажем, что и будет наибольшим значением функции f(x) на отрезке [a,b]: .

Предположим противное, то есть .

Так как , то f(x)< .

-f(x)>0

введем в рассмотрение функцию . Функция непрерывна на [a,b], так как -f(x)0. Тогда, в силу первой теоремы Вейерштрасса, функция ограничена на [a,b].

<M > , где >0

Так как данное неравенство выполняется , то число не является точной верхней гранью множества значений функции. Приходим к противоречию, значит, наше предположение неверно. Аналогично можно доказать, что непрерывная функция достигает на отрезке своего минимального значения. Теорема доказана.

3. Дифференцируемые функции Теоремы Ролля и Лагранжа. Формула Тейлора с остаточным членом в форме Лагранжа.

Теорема Ролля. Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если

f(a) = f(b)

то внутри интервала [а, b] найдется хотя бы одно такое значение x₀ (a < x₀ < b), что

f ' (x₀) = 0.

Доказательство. Рассмотрим два случая.

1. Функция f(x) постоянна на интервале [а, b]; тогда f ' (x) = 0 для любого x (a < x < b), т.е. утверждение теоремы Ролля выполняется автоматически.

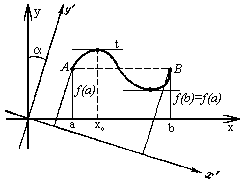
2. Функция f(x) не является постоянной (Рисунок 1); тогда наибольшего или наименьшего или обоих этих значений она достигает во внутренней точке интервала, ибо f(b) = f(a), и если f(a) - наименьшее значение, то наибольшее значение значение функция f(x) примет внутри интервала.

Рис.1

Пусть например f(x₀) - наибольшее значение функции f(x) на интервале [а, b] и x₀ - внутренняя точка этого интервала. Тогда f(x₀) является максимумом функции: f(x₀)  f(x) для всех x из достаточно малой окрестности x₀ [за эту окрестность можно впрочем, взять интервал (а, b)].

Так как, по условию, f(x) имеет в точке x₀ производную, то по теореме о необходимом признаке экстремума,

f ' (x₀) = 0,

и теорема Ролля доказана.

Теорема Ролля имеет простое геометрическое толкование: если дана дуга AB кривой y = f(x), в каждой точке которой существует касательная, причем концы A и B находятся на одинаковом расстоянии от оси Ox, то на этой дуге найдется по крайней мере одна точка, в которой касательная t к кривой будет параллельна стягивающей дугу хорде, а следовательно и оси Ox (смотри рисунок 1).

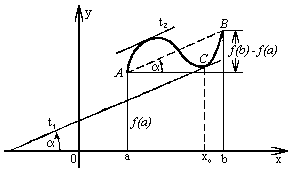
Если повернуть оси координат на угол a, то концы A и B дуги AB уже не будут находится на одинаковом расстоянии от оси Ox', но касательная t по прежнему будет параллельна хорде AB (смотри рисунок 1). Поэтому естественно ожидать, что имеет место теорема: Если дана дуга AB кривой y = f(x) с непрерывно изменяющейся касательной, то на этой дуге найдется хотя бы одна точка, в которой касательная параллельна стягивающей ее хорде AB (Рисунок 2).

Рис.2

Эта теорема является геометрической перефразировкой следующей теоремы, известной под названием теоремы Лагранжа.

Теорема Лагранжа. Если функция f(x) непрерывна на замкнутом интервале [а, b] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x₀ (a < x₀ < b), что

f(b) - f(a) = (b - a)f '(x).

Доказательство. Рассмотрим вспомогательную функцию

F(x) = f(x) - k(x - a),

где - угловой коэффициент хорды AB (смотри рисунок 2).

Эта функция удовлетворяет всем условиям теоремы Ролля.

В самом деле, при x = a имеем F(a) = f(a) - k(a - a) = f(a), при x = b имеем

Кроме того, так как функция f(x) и k(x - a) непрерывны на [a, b] и диференцируемы в (a, b), то и функция F(x) = f(x) - k(x - a) непрерывна на [a, b] и диференцируема в (a, b).

Следовательно, по теореме Ролля, в интервале (a, b) найдется такая точка x₀, что

F'(x₀) = 0,

т.е.

f ' (x₀) - k = 0

или

Отсюда имеем

f(b) - f(a) = (b - a)f ' (x₀),

что и требовалось доказать.

Так как a + (b - a) = b, то величина a + (b - a), где Q - правильная положительная дробь (0 <  < 1), равна какому-то числу в интервале (a, b), поэтому формулу Лагранжа можно записать в виде

f(b) - f(a) = (b - a)f ' [a + (b - a)]

Если положить a = x, b = x + x, откуда b - a = x, то формула Лагранжа запишется в виде

y = f(x + x) - f(x) = xf ' (x + x).

Ранее было доказано, что если функция равна постоянной C при любом значении x в интервале (a, b), то ее производная равна нулю.

Докажем теперь обратную теорему, являющуюся следствием теоремы Лагранжа:

Если произвоодная f ' (x) обращается в нуль для любых значений x в интервале (a, b), то в этом интервале f(x) = C.

В самом деле, если x₁ и x₂ - два любых значения в интервале (a, b), то в силу теоремы Лагранжа, имеем

f(x₂) - f(x₁) = (x₂ - x₁)f'(x₀),

где, x₁ < x₀ < x₂. Но так как f'(x₀) = 0, то

f(x₂) - f(x₁) = 0,

что и доказывает нашу теорему.

Отсюда непосредственно вытекает важная теорема:

Если две функции f₁ (x) и f₂ (x) имеют одну и ту же производную в интервале (a, b), то они на данном интервале отличаются друг от друга на постоянную величину.

В самом деле, рассмотрим функцию

(x) = f₂(x) - f₁(x).

Тогда для любого значения x из интервала (a, b)

'(x) = f₂'(x) - f₁'(x) = 0.

Но это означает, что (x) = C и, следовательно

f₂(x) - f₁(x) = С.

Формула Тейлора. Пусть на интервале [a, b] функция f(x) дифференцируема n раз и выполняются следующие равенства:

f(a) = f(b) = f '(a) = f ''(a)= ... = f ^(n-1)(a)=0

Тогда внутри интервала [a, b] найдется хотя бы одно значение с, при котором

f ⁽ⁿ⁾(c) = 0

Доказательство. По теореме Ролля имеем

f '(x₀ ) = 0,

где a < x₀ < b. Тогда f '(x) на интервале [a, x₀] удовлетворяет теореме Ролля, так как, по условию, f '(a) = 0 и f '(x₀ ) = 0, а потому

f ''(x₁ ) = 0,

где a < x₁ < x₀.

Применяя теорему Ролля последовательно к функциям f ''(x), f '''(x), ..., f ^(n-1)(x), найдем наконец:

f ⁽ⁿ⁾(с) = 0,

где a < c < x_n-1 < b . Теорема доказана.

Выведем теперь формулу Тейлора с остаточным членом в форме Лагранжа.

Пусть функция f (x) дифференцируема n раз на интервале [a, b].

Рассмотрим вспомогательную функцию

(x) = f (x) - P (x),

где

Продифференцируем n раз функцию (x). Тогда будем иметь

. . . . . . . . . . . . . . . . . . . . . . . . . . . .

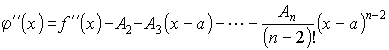^(n-1)(x) = f^(n-1)(x) - A_n-1 - A_n(x - a),

⁽ⁿ⁾(x) = f⁽ⁿ⁾(x) - A_n

Потребуем, чтобы функция (x) удовлетворяла условиям обобщенной теоремы Ролля. Тогда будем иметь

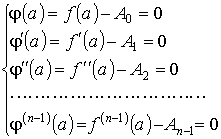(1) .

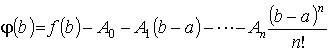Так как функция (x) удовлетворяет условиям обобщенной теоремы Ролля, то найдется такое значение с (a < c < b), что

⁽ⁿ⁾(с) = f⁽ⁿ⁾(с) - A_n = 0 (2)

Далее найдем из n первых уравнений системы (1) коэффициенты A₀ , A₁ , ..., A_n-1:

A₀ = f(a), A₁ = f'(a), A₂ = f''(a), ..., A_n-1 = f^(n-1)(a),

а из уравнения (2) коэффициент A_n: A_n = f⁽ⁿ⁾(c) и подставим их значения в последнее уравнение системы (1):

,

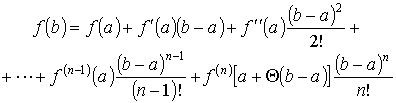где 0 <  < 1

Заменяя b на x, получим формулу Тейлора:

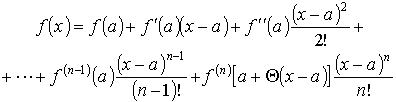
где 0 <  < 1

Последнее слагаемое

называется остаточным членом в форме Лагранжа.

При a = 0 получается так называемая формула Маклорена:

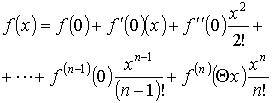
где 0 <  < 1, а остаточный член записывается в виде