5. Функции многих переменных. Дифференцируемость функций многих переменных. Теорема о достаточных условиях дифференцируемости функции.

Пусть определена в некоторой окрестности точки , - точка из этой окрестности.

Определение 1 Величина называется приращением функции в точке, соответствующим приращению аргумента .

Определение 2 Функция называется дифференцируемой в точке , если существуют такие постоянные числа и функции при (1)

Часто обозначают и . Тогда (1) перепишем в виде .

При наше определение (1) совпадает с известными из материала 1-го семестра определением дифференцируемости . Для функций одной переменной дифференцируемость равносильна существованию производной. В случае нескольких переменных ситуация несколько сложнее.

Сначала введем в рассмотрение величину . Она представляет собой приращение функции при фиксированных значениях всех производных, кроме i-той.

Пусть дифференцируема в точке . Тогда для любого равенство (1) дает при (2)

Поскольку при фиксированных значениях равносильно тому, что , равенство (18.2) означает, что функция одной переменной .

дифференцируема в точке и, значит, существует (3) называемый, по определению, частной производной функции по переменной в точке .

Мы только что, тем самым, доказали теорему:

Теорема1. Если дифференцируема в точке , то для всех существуют .

Таким образом, существование частных производных – необходимое условие дифференцируемости. При этом при .

Другое необходимое условие дифференцируемости – непрерывность функции, как показывает следующая теорема.

Теорема2. Если дифференцируема в точке , то .

Доказательство. Достаточно доказать, что при , , (т.к. ). Но это сразу следует из равенства (1), так как .

Однако, в отличие от случая , из существования частных производных ,определенных равенством (3) не следует даже непрерывность функции в точке и тем более не следует дифференцируемость в точке , согласно теореме(2).

Пример. 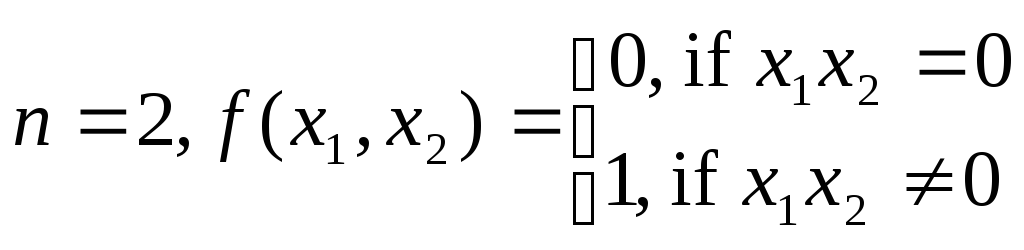. Тогда , так как . Аналогично, . Однако даже не непрерывна в точке .

Достаточное условие дифференцируемости дает следующая теорема.

Теорема. Пусть частные производные существуют в окрестности точки и непрерывны в этой точке. Тогда дифференцируема в точке .

Доказательство. Пусть принадлежит рассматриваемой окрестности . При этом все точки так же принадлежат рассматриваемой окрестности. Приращение функции представим в виде (4)

и рассмотрим разности (5) составляющие в сумме приращение (4).

Положим (то есть фиксируем все переменные, кроме ). Тогда рассматриваемая разность (5) имеет вид . Функция по условию дифференцируема на отрезке, соединяющим и . Значит, она непрерывна на этом отрезке и можно применить теорему Лагранжа, согласно которой , где .

Но . По условию непрерывности частных производных , где при .

Поэтому каждая из разностей (5) имеет вид , а приращение (4) совпадает с (3) из определения дифференцируемости. Теорема доказана.

Замечание 1. Непрерывность частных производных не является необходимым условием дифференцируемости функций. Например можно доказать, что функция 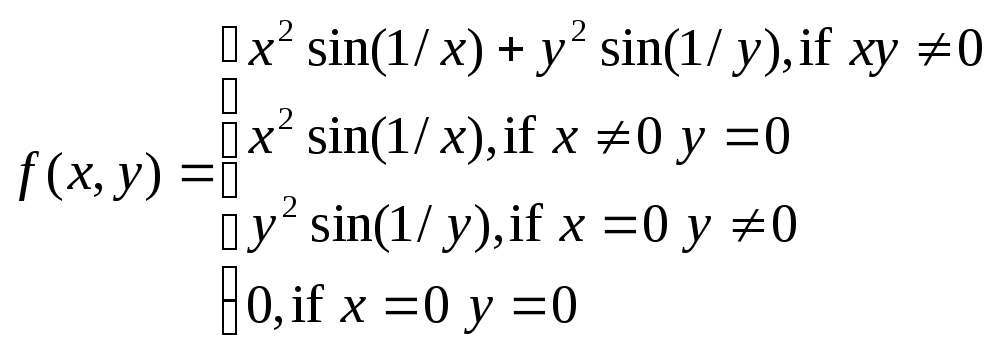дифференцируема в точке , но частные производные в этой точке не непрерывны.

Замечание 2. Тем не менее, для функции частные производные в точке равны 0, так как и (в остальных точках , и ясно, что эти производные терпят разрыв в точке . Но при1ращение не имеет вид , где при . Действительно, полагая и предполагая, что получаем , или что ншевозможно, так как при правая часть стремится к 0, а левая нет!

6. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ. Равномерная и поточечная сходимости функциональных последовательностей и рядов. Почленное дифференцирование и интегрирование функциональных рядов. Степенные ряды. Теорема Коши-Адамара о радиусе сходимости степенного ряда. Почленное дифференцирование и интегрирование степенных рядов (как следствия).

Отображение множества натуральных чисел N во множество действительных функций одного переменного x, определенных на промежутке I, называется функциональной последовательностью и обозначается

{ f_n (x ) } илиf₁ (x ),f₂ (x ),f₃ (x…; (3) ),

функции f_n (x) называются членами последовательности. Каждое значение x ∈ I, для которого последовательность (3) имеет некоторый (конечный) предел, принадлежит области сходимости этой последовательности. Таким образом, последовательность определяет в области сходимости некоторую функцию

f (x) = f_n (x),

которая называется предельной функцией (или пределом) последовательности. В дальнейшем предполагаем, что область сходимости совпадает с областью определения I.

Для того чтобы охарактеризовать предельную функцию, используют понятие равномерной сходимости. Функциональная последовательность сходится к предельной функции f (x) равномерно в I, если для любого ε > 0 найдется такое N (ε), не зависящее от x, что для всех n > N (ε) и для всех x ∈ I выполняется неравенство

| f_n (x) – f (x)| < ε.

Обозначение: f_n (x) f (x).

Если существует такое ε > 0, что для каждого числа N имеется по меньшей мере одно n > N и x₀ ∈ I такие, что | f_n (x₀) – f (x₀)| > ε, то говорят, что последовательность сходится неравномерно.

Критерий Коши равномерной сходимости функциональной последовательности. Последовательность (3) сходится равномерно в I тогда и только тогда, когда для каждого ε > 0 существует не зависящее от x число N (ε) такое, что при n ≥ N и для любого m ≥ N

| f_{n + m} (x) – f_n (x)| < ε для всех x ∈ I одновременно.

Функциональные ряды. Бесконечный ряд, построенный из функциональной последовательности

f_n (x) = f₁ (x) + f₂ (x) + … + f_n (x) + …

называется функциональным рядом. Понятия «область сходимости», «предельная функция» и «равномерная сходимость» переносятся на функциональную последовательность частичных сумм S_n (x) = f_s (x). Разность между суммой S (x) сходящегося функционального ряда и одной из его частичных сумм S_n (x) называют остатком и обозначают

R_n (x) = S (x) – S_n (x) = f_s (x).

Признак Вейерштрасса равномерной сходимости рядов. Ряд f_n (x) сходится на промежутке I равномерно, если существует сходящийся числовой ряд a_n с положительными членами такой, что для всех n ≥ N и всех x ∈ I выполняется неравенство

| f_n (x) | ≤ a_n.

Ряд a_n называется мажорантой функционального ряда f_n (x).

Признак Абеля равномерной сходимости рядов. Ряд a_n (x) b_n (x) сходится для всех x ∈ I равномерно, если ряд b_n (x) сходится в I равномерно и для каждого x ∈ I последовательность {a_n (x)} является монотонной и ограниченной.

Признак Дирихле равномерной сходимости рядов. Ряд a_n (x) b_n (x) сходится для всех x ∈ I равномерно, если частичные суммы (x) = b_k (x) равномерно ограниченны: | (x)| ≤ M, M = const, и если последовательность {a_n (x)} монотонно и равномерно стремится к нулю.

Степенной ряд есть функциональный ряд с общим членом f_n (y) = a_n( y – y₀ )ⁿ (n = 0, 1, 2, …) (a_n — действительные числа):

a_n( y – y₀ )ⁿ = a₀ + a₁( y – y₀ ) + a₂( y – y₀ )² + … + a_n( y – y₀ )ⁿ + …

Действительное число y₀ называется центром степенного ряда. Заменой переменного x = y – y₀ этот степенной ряд преобразуется в степенной ряд

a_n xⁿ = a₀ + a₁ x + a₂ x² + … + a_n xⁿ + …

с нулевым центром. В дальнейшем ограничимся исследованием рядов именно такого вида.

Существуют степенные ряды, которые

а) сходятся при всех x (всюду сходящиеся степенные ряды), например ;

б) сходятся только при x = 0, например n! xⁿ;

в) для некоторых x ≠ 0 сходятся, для других расходятся, например xⁿ.

 Если степенной ряд a_n xⁿ при некоторых x ≠ 0 сходится, а при остальных расходится, то существует, и притом только одно, положительное число r такое, что степенной ряд при | x | < r сходится, и даже абсолютно, а при | x | > r расходится. При x = r и x = – r ряд может как сходиться, так и расходиться. Число r называют радиусом сходимости степенного ряда. Если r > 0, то промежуток (– r, r) называется интервалом сходимости степенного ряда.

Для вычисления радиуса сходимости используется теорема Коши – Адамара: радиус r сходимости ряда a_n xⁿ равен обратной величине верхнего предела последовательности {}:

r =

(при этом r = ∞, если = 0, и r = 0, если = ∞).

Верхний предел r числовой последовательности {b_n} есть верхняя граница «сгущения» последовательности, т. е. для любого ε > 0 существует только конечное число индексов n таких, что b_n > r + ε, но для бесконечного числа n справедливо неравенство b_n > r – ε. Если для любого действительного числа C имеется бесконечное множество индексов n таких, что b_n > C, то говорят, что верхний предел равен + ∞; если напротив, имеется только конечное число индексов n таких, что b_n > C, то говорят, что верхний предел равен – ∞. Верхний предел существует всегда. Если существует , то

= .

Радиус сходимости r степенного ряда a_n xⁿ может быть вычислен также при помощи признака Даламбера: если существует предел = q, то r = (r = ∞ при q = 0 и r = 0 при q = ∞).

Почленное интегрирование и дифференцирование ряда

Теорема 2.1. Степенной ряд (1.2) сходится равномерно на любом отрезке, целиком содержащемся внутри интервала сходимости.

Доказательство. Пусть степенной ряд имеет интервал сходимости (-R,R). Рассмотрим какой-нибудь отрезок целиком содержащимся в (-R,R). Очевидно, что всегда можно найти отрезок вида , содержащий и целиком лежащий в (-R,R). Если , то и, следовательно, члены ряда (3.2) не превосходят по модулю членов ряда

Но последний ряд сходится, так как r<R. Таким образом, согласно признаку Вейерштрасса, ряд (3.2) сходится равномерно на отрезке

Теорема доказана.

Теорема. (непрерывность суммы ряда). На любом отрезке целиком лежащем внутри интервала сходимости степенного ряда (1.2), сумма ряда есть непрерывная функция.

Доказательство. Каждая частичная сумма степенного ряда, очевидно, является непрерывной функцией. По теореме 2.1 на любом отрезке целиком лежащем внутри интервала сходимости ряда сходимость является равномерной. Сумма ряда, являющаяся пределом равномерно сходящейся последовательности непрерывных функций, сама является непрерывной функцией. Теорема доказана.

Теорема. (Почленное интегрирование степенного ряда). Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.

Теорема. (Почленное дифференцирование степенного ряда). Пусть степенной ряд

(1)

имеет радиус сходимости R. Тогда ряд

(2)

полученный в результате почленного дифференцирования ряда (1), также имеет радиус сходимости R. Производная суммы ряда (1) равна сумме ряда:

Из теоремы 2.4 следует

Теорема. Степенной ряд в пределах его интервала сходимости можно дифференцировать почленно любое число раз. При этом радиусы сходимости всех рядов, полученных дифференцированием данного ряда, совпадают с радиусом сходимости этого ряда.