4. Интегрирование. Интеграл Римана. Теорема об интегрируемости непрерывной функции. Теорема о непрерывности и дифференцируемости интеграла с переменным верхним пределом. Формула Ньютона-Лейбница.

Пусть действительная функция f(x) определена и ограничена на ограниченном замкнутом интервале [a, b]. Разобъем этот интервал на n частичных интервалов точками

a = x₀ < x₁ < x₂ < ... < x_n = b.

Выберем в каждом из частичных интервалов по произвольной точке и составим сумму (интегральная сумма) .

Если существует предел интегральной суммы при стремлении к нулю длины наибольшего частичного интервала разбиения: , то функция f(x) называется интегрируемой в смысле Римана на интервале [a, b]. Предел этой суммы

называется определенным интегралом от f(x) по интервалу [a, b] в смысле Римана (интеграл Римана). Это определение означает, что для любого положительного числа существует такое число , что при любом разбиении интервала [a, b] на частичные интервалы, длины которых меньше .

и при любом выборе промежуточных точек выполняется неравенство

Функция f(x) называется подынтегральной функцией, а a и b - пределами интегрирования.

Интегрируемость непрерывных функций

Докажем следующую основную теорему.

Теорема. Непрерывная на сегменте [a, b] функция f(x) интегрируема на этом сегменте.

Доказательство. Пусть дано любое ε > 0. В силу равномерной непрерывности функции f(x) на сегменте [a, b] для положительного числа ε/(b - a) можно указать такое δ > 0, что при разбиении T сегмента [a, b] на частичные сегменты [x_i-1, x_i], длины Δx_i которых меньше δ, колебание ω_i функции f(x) на каждом таком частичном сегменте будут меньше ε/(b - a) (см. следствие из теоремы о равномерной непрерывности), Поэтому для таких разбиений T

Следовательно, для непрерывной на сегменте [a, b] функции f(x) выполнены достаточные условия интегрируемости.

Интеграл с переменным верхним пределом

Рассмотрим функцию , заданную на отрезке , и предположим, что она интегрируема на отрезке . Тогда при любом эта функция будет интегрируема на отрезке и, следовательно, функция

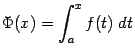
определена при всех . При мы по определению положим её равной 0, то есть будем считать, что для любой функции и точки из её области определения. Итак, функция равняется значению определённого интеграла с переменным верхним пределом, вычисленного от интегрируемой функции , не обязательно непрерывной.

Теорема Функция , определённая выше, непрерывна при всех для любой интегрируемой функции .

Доказательство. Заметим, что если функция положительна, то значение интерпретируется как площадь под графиком , лежащая над отрезком . Если дать приращение , то площадь получит приращение в виде площади полоски, лежащей над отрезком (см. рис.).

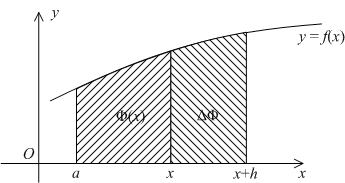
Рис..

Эта площадь, вследствие ограниченности интегрируемой функции, мала, если приращение мало; это и означает непрерывность функции в точке .

Теорема Пусть функция непрерывна на отрезке и функция определена всё той же формулой. Тогда имеет производную в любой точке интервала , производную справа в точке и производную слева в точке , причём эти производные совпадают со значением функции в соответствующей точке:

при и

Доказательство. Снова рассмотрим приращение при , , . Поскольку функция непрерывна, мы можем применить теорему о среднем к интегралу по отрезку :

где -- некоторая точка отрезка . Получаем, деля на :

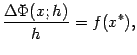
откуда при из непрерывности следует, что

поскольку при . Получили, что правая производная совпадает с во всех точках .

Аналогично доказывается, что левая производная совпадает с во всех точках Во внутренних точках совпадение производных слева и справа со значением означает, что функция имеет производную , равную .

Точно так же доказывается, что производная интеграла

от непрерывной функции по переменному нижнему пределу равняется :

Равенство означает, что функция является первообразной для на интервале . Другая первообразная -- это, очевидно, функция .

Теорема. (Формула Ньютона-Лейбница). Если , то для любой первообразной имеет место равенство .

Доказательство. По доказанному следствию, первообразная существует. Если – любая другая первообразная, то существует такая, что , т.е. .

Тогда , что и требовалось доказать.