Лекции / семестр3 / Альшина (МП-2) / Pr8

§14. Ряды аналитических функций.

1. Понятие функционального ряда. Пусть дана последовательность {u _k(z)} функций, z  g. Выражение - называется функциональным рядом, заданным в g. Определение.Если при z  g, соответствующий числовой ряд сходится к определенному комплексному числу f(z), то в g определена функция, которая называется суммой функционального ряда, а сам ряд называется сходящимся в g.

r_n(z)=f(z)- - n-ый остаток ряда

Если ряд сходится в g, то

>0  N(,z): | r_n(z)| <для n > N(, z).

Пример.

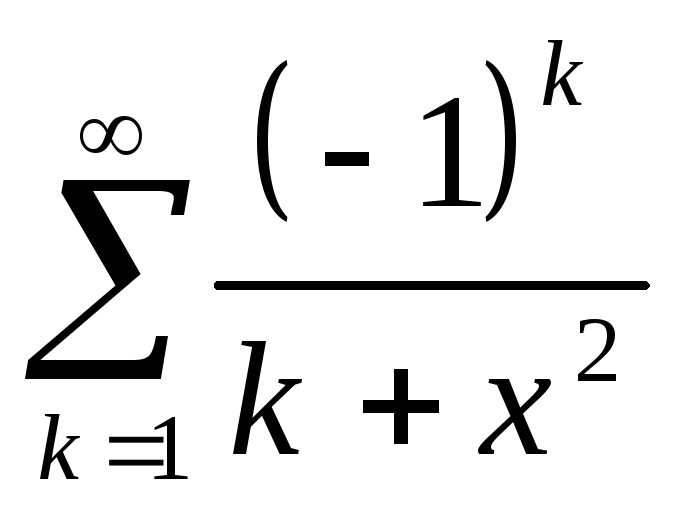- знакочередующийся ряд, сходится и признаку Лейбница, остаток ряда не превышает модуля следующего слагаемого

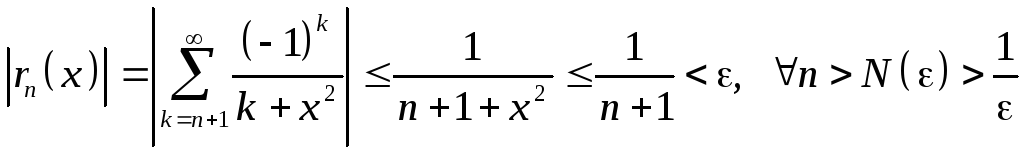
Необходимый и достаточный признак сходимости: Критерий Коши: для >0  N( ,z): | S_n+m(z)-S_n(z)| <для n > N и m>0. Вообще говоря, в каждой точке z  g N свое: N=N( ,z) и общего N для всей z может и не существовать.

2. Равномерная сходимость u_k(z) в области g. Определение. Если для >0  N() : | r_n(z)| <для n >N() и  z одновременно, то ряд u_k(z) называется равномерно сходящимся к функции f(z) в g. Обозначение: u_k(z)=>f(z).

Критерий Коши (необходимое и достаточное условие равномерной сходимости).

Если для >0  N( ): | S_n+m(z)-S_n(z)| <для n > N и m>0 и  z одновременно, то ряд u_k(z)=>f(z). Доказательство. Необходимость.

Пусть u_k(z)=>f(z)  >0  N(): |f(z)-S_n(z)| < /2 для n>N() и zg => и |f(z)-S_n+m(z)| < /2 => =>| S_n+m(z)-S_n(z)| <для n>N и m>0 и zg. Достаточность. Пусть для >0  N( ): | S_n+m(z)-S_n(z)| < для n>N и m>0 и zg => сходится в zg, т.о. в g определена f(z)=.

для n>N() и zg => |r_n(z)| <для n>N() и zg. 

Признак Вейерштрасса (достаточный признак равномерной сходимости). Если |u_k(z)|<a_k, a_k>0 для k>N и zg и a_k сходится, то u_k(z)=>f(z) в g. Доказательство.

a_k сходится => >0  N(): < для n>N()

для n>N() и zg. 

Примеры.

1. 

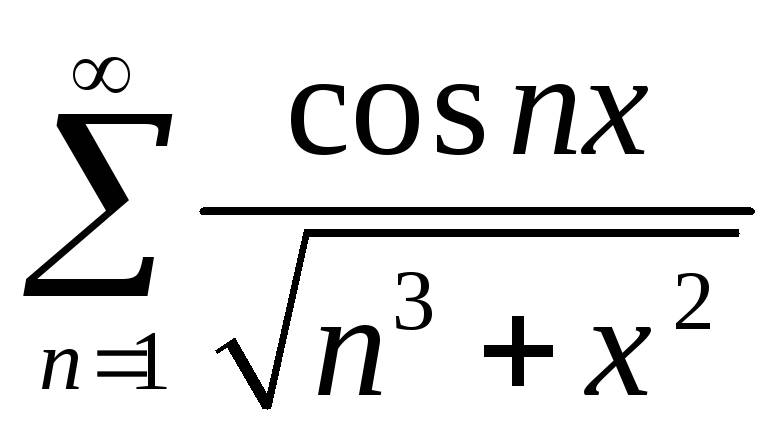
2. (оценить сверху значением функции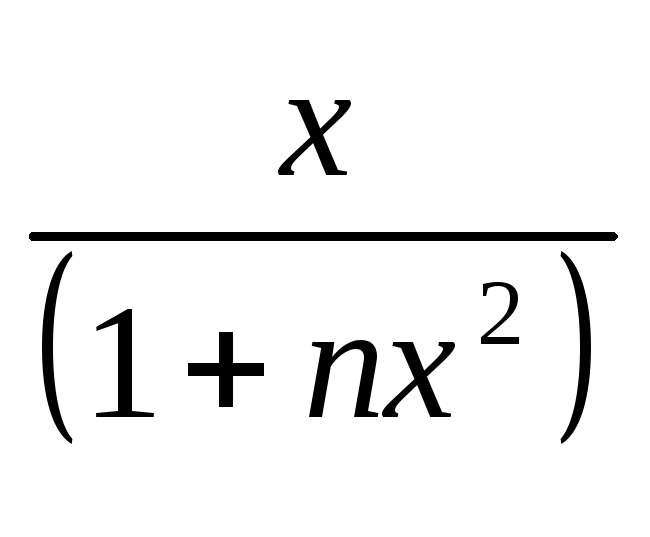 в ее максимуме)

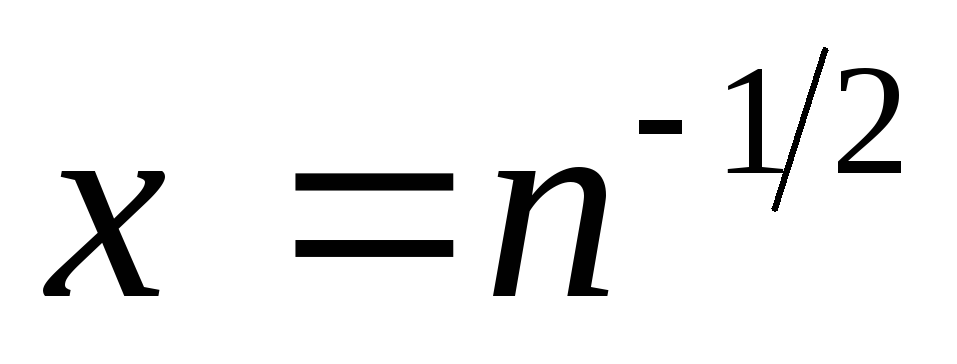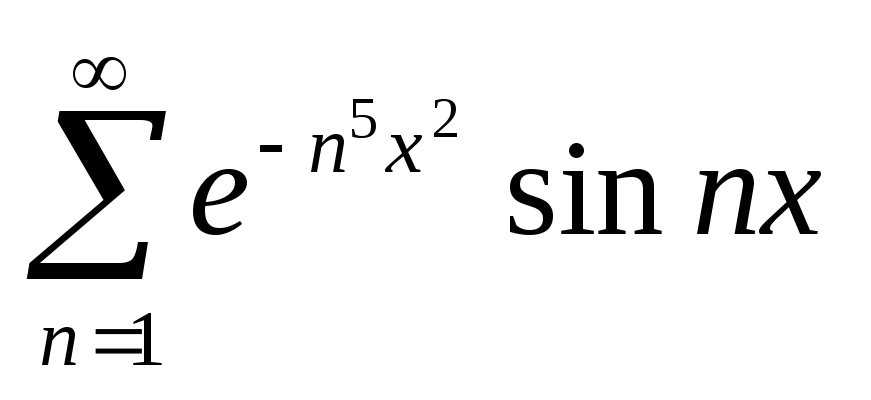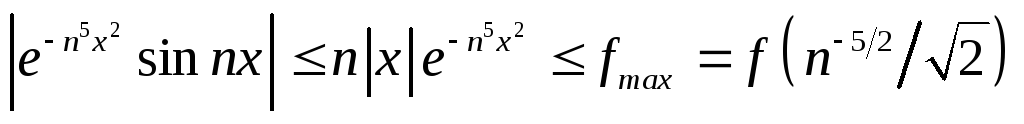3. (оценить сверху значением функции в ее максимуме )

4. () 3. Свойства равномерно сходящихся рядов. Свойства равномерно сходящихся рядов: Теорема 14.1. (непрерывность суммы) Пусть u_k(z)С(g) и u_k(z)=>f(z), тогда f(z)С(g). Доказательство.

u_k(z)=>f(z)  одновременно выполнены неравенства

|f(z+z)-S_n(z+z)|< /3 и |f(z)-S_n(z)|< /3 для >0.

u_k(z)С(g)  для >0 и N  >0:

при |z|<

 |f|=|f(z+z)-f(z)|

|f(z+z)-S_n(z+z)|+|S_n(z+z)-S_n(z)|+|S_n(z)-f(z)| 

/3+/3+/3=для |z|< , n>N.

Примеры

1. Ряд из непрерывных функций сходится к разрывной функции, значит сходимость неравномерная

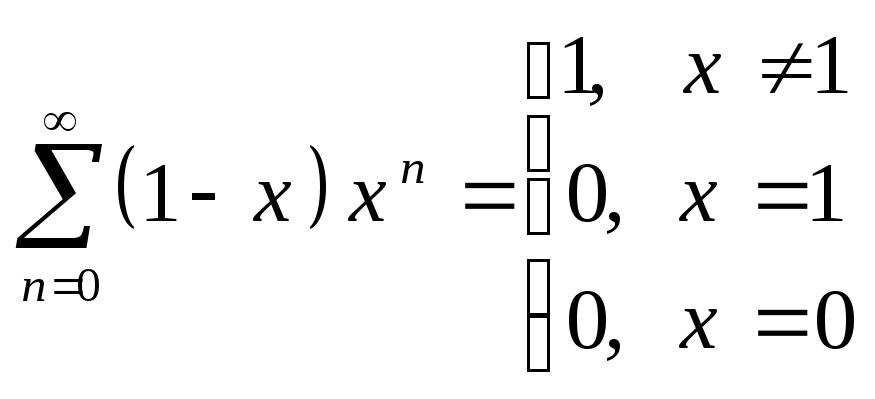2. аналогично

Теорема 14.2. (возможность почленного интегрирования). Пусть u_k(z)С(g) и u_k(z)=>f(z),  кусочно- гладкий контур g конечной длины L. Тогда .

Доказательство

u_k(z)=>f(z) 

для >0  N(): | r_n(z) |</L для n>N()

=<=

Замечание. Эти два свойства равномерно сходящихся рядов с комплексными членами совершенно аналогичны свойствам равномерно сходящихся функциональных рядов с действительными членами.

Примеры.

1. Найти , если

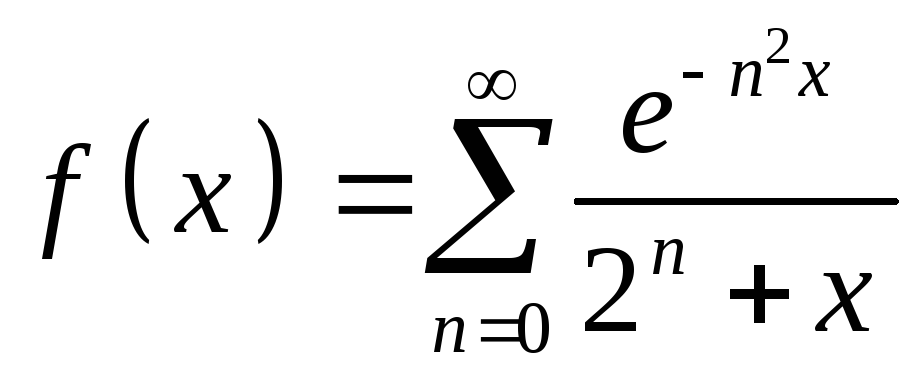
2. Является ли непрерывной функция

3. 

4. 

5. 

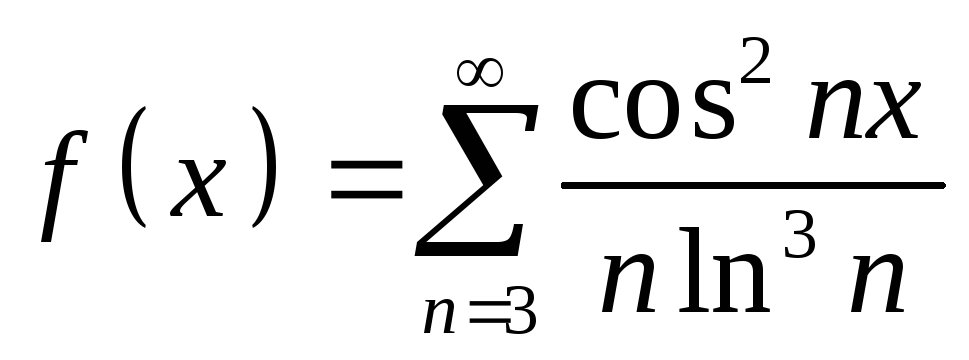
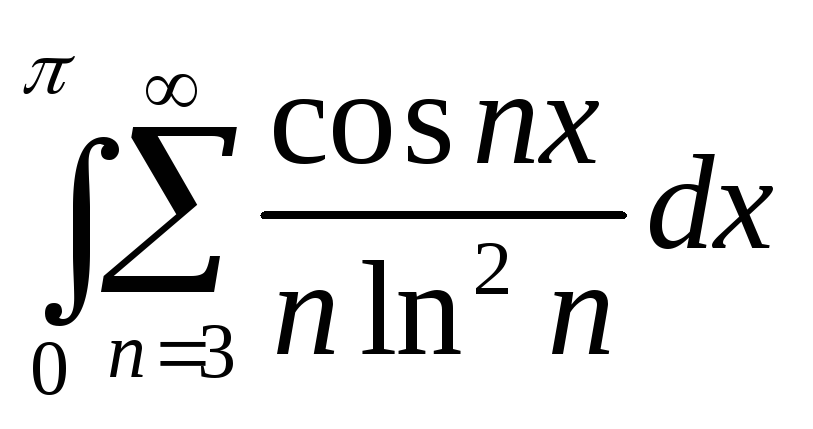
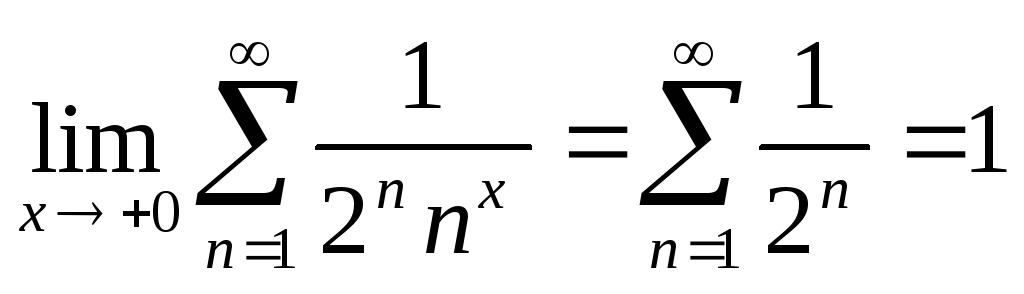
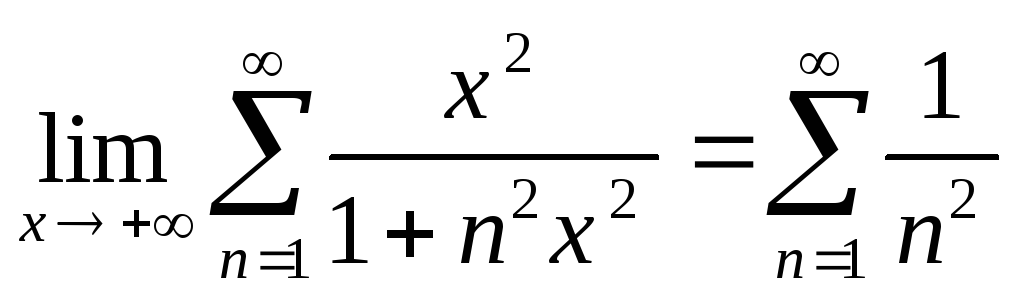
Теорема Вейерштрасса. Если u_k(z)C^(g) и u_k(z)=>f(z) в любой замкнутой подобласти области g то:

1. f(z)C^(g).

2. , для zg.

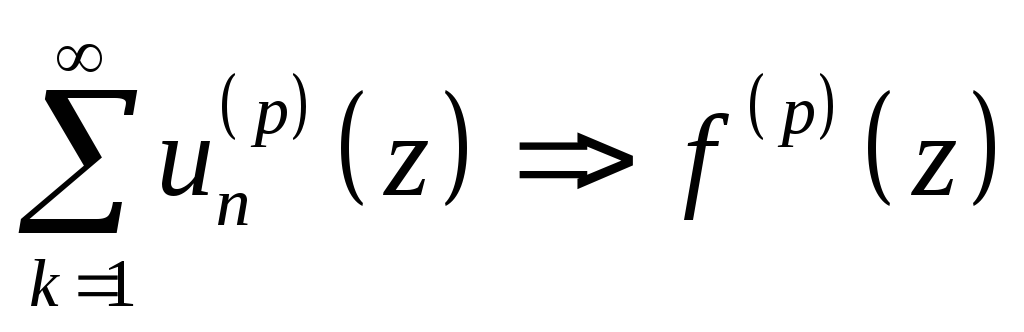3. z .

Доказательство 1. Рассмотрим произвольную z₀g и построим односвязную : z₀, в силу Теоремы 14.1 f(z)С(g).

Рассмотрим произвольный контур . По Теореме 14.2 .

Т.о. для f(z) выполнены все условия Теоремы Морера  f(z)C^(). В силу произвольности f(z)C^(g).

Замечание. Т.к. r_n(z)=f(z)-S_n(z)  r_n(z) C^(g).

2. Рассмотрим произвольную z₀g и произвольный контур g. Обозначим .

для  z, т.к.

По Теореме 14.2 это равенство можно проинтегрировать почленно

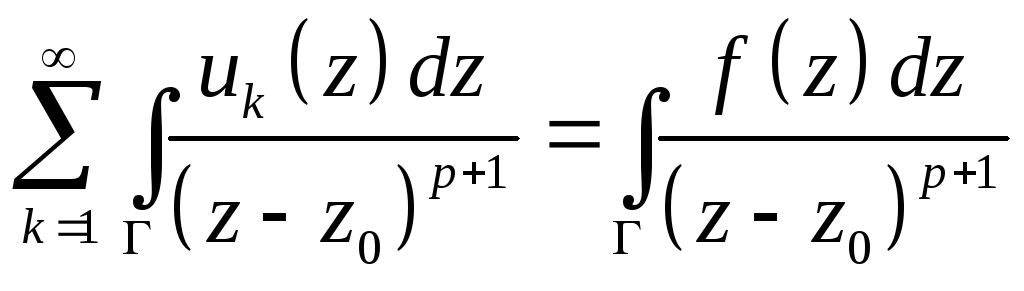
По Теореме 8.1.

.

В силу произвольности z₀ утверждение 2 доказано.

Замечание. r_n^(p)(z)=f^(p)(z)-S_n^(p)(z)=.

3. Рассмотрим  и  - замкнутый контур: g и z и  |z-|d>0.

r_n(z) C^(g) 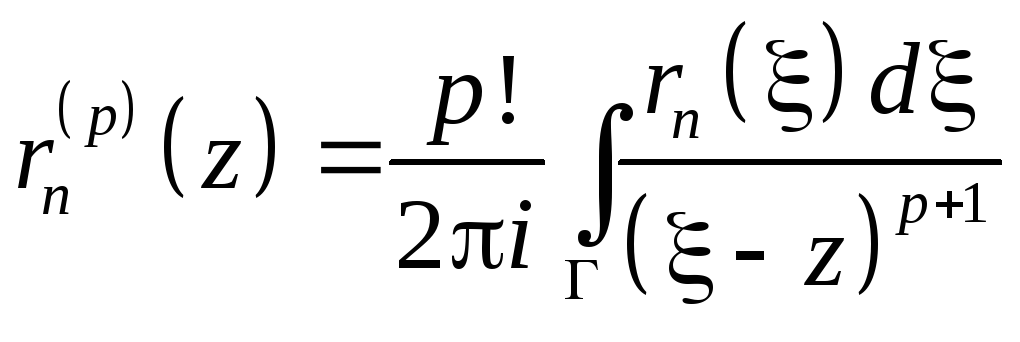 для z .

u_k(z)=>f(z)  >0  N(): , где L- длина .

Тогда .

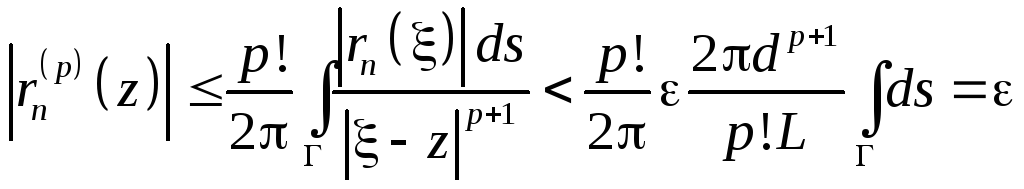Т.о. получена равномерная оценка для остатка ряда для производных  .

Пример. Ряд z^k/k² сходится равномерно в круге |z|1, а ряд из производных z^k-1/k не может равномерно сходится в этом круг, т.к. он расходится при z=1. Ряд z^k-1/k равномерно сходится при |z|<1.

Для равномерно сходящихся функциональных рядов с действительными членами верна

Теорема 14.3. Пусть u_k(x) – непрерывно дифференцируемы на отрезке [a,b] и ряд, составленный из производных - равномерно сходится на отрезке [a,b], тогда если ряд сходится хотя бы в одной точке c[a,b], то он равномерно сходится на всем отрезке [a,b], его сумма непрерывно дифференцируема и .

Доказательство.

Пусть (непрерывна в силу равномерной сходимости ряда).

Найдем первообразную

для . Ряд сходится по условию теоремы  тоже сходится на всем промежутке.

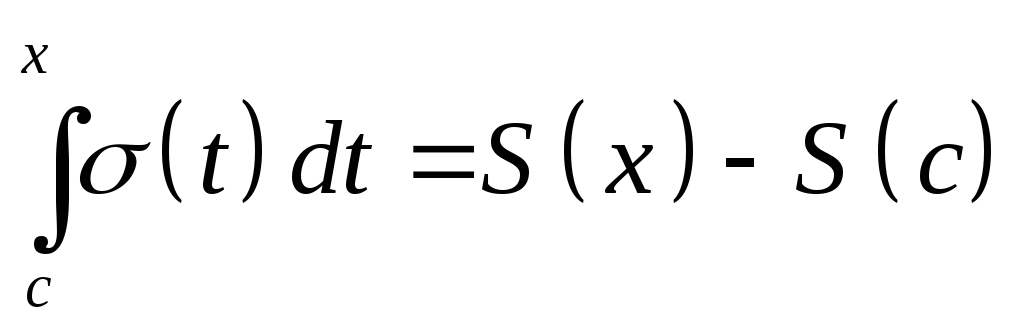
Левая часть равенства имеет производную по x S(x)=(x) и

сходится равномерно, т.к. первый ряд справа сходится равномерно, а второй не зависит от x.

Примеры.

1. Равномерно сходящийся на всей действительной оси ряд дифференцировать нельзя, так как ряд из производных расходится, например при x=0.

2. (1+1+1+1+…)=0+0+0+0+… Ряд, полученный в результате формального дифференцирования, сходится и даже равномерно, но дифференцирование не правомерно, т.к. исходный ряд расходится.

3. почленное дифференцирование возможно в силу равномерной сходимости ряда из производных.

4