

Лекция 3
3. Понятие предела функции комплексной переменной. Непрерывность функции комплексного переменного.
Определение: Пределом функции f(z) в точке z0, называется комплексное число w0, такое, что 8" > 0 9±("; z0) > 0 такое, что при 0 < jz ¡ z0j < ± выполняется соотношение jf(z) ¡ w0j < ". Записывают:
lim f(z) = w0
z!z0
Определение: Предел функции f(z) в точке z0 равен бесконечности, если 8A 2 R 9±(A) > 0, такое, что 0 < jz ¡ z0j < ± выполняется соотношение jf(z)j > A. Записывают:
lim f(z) = 1
z!z0
Определение: Предел функции f(z) ïðè z ! 1 равен комплексному числу
w0, åñëè 8" > 0 9R > 0, такое, что jzj > R выполняется соотношение jf(z) ¡ w0j < ". Записывают:
lim f(z) = w0
z!1
Теорема 3.1: Необходимым и достаточным условием того, что число w0 = u0 + iv0 - предел функции f(z) = f(x + iy) = u(x; y) + iv(x; y) в точке z0 = x0 + iy0 является существование пределов
lim u(x; y) = u0; |
lim v(x; y) = v0 |
x!x0;y!y0 |
x!x0;y!y0 |
рассматриваемых по совокупности переменных. Доказательство:
Необходимость: 8" > 0 9±(") ÷òî jf(z) ¡ w0j < " ïðè jz ¡ z0j < ± =)
ju(x; y) ¡ u0j · jf(z) ¡ w0j < " è jv(x; y) ¡ v0j · jf(z) ¡ w0j < " =) ïðè |
|||||||||||||||
p |
|
|
определением предела по совокупности переменных для функций |
||||||||||||
½ = |
(x ¡ x0)2 |
+ (y ¡ y0)2 < ± имеем ju(x; y)¡u0j < " è jv(x; y)¡v0j < " ÷òî |
|||||||||||||
является |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u(x; y) è v(x; y). |
|
|
|
|
|
|
|
|
|
|
|||||
Достаточность: 8" > 0 9±1(") ÷òî ju(x; y) ¡ u0j < 2" |
ïðè |
|
|
|
|||||||||||
а также |
´ p |
|
|
|
|
|
" |
|
|
|
|
|
|||
|
÷òî |
|
|
|
|
|
|
|
|
||||||
½1 |
|
(x ¡ x0)2 + (y ¡ y0)2 |
< ±1; |
|
|
|
|
|
|||||||
|
|
9±2(") |
|
|
jv(x; y) ¡ v0j < 2 ïðè |
|
|
|
|
|
|||||
Выбирая´ p |
|
|
|
|
|
|
|
|
2 |
2 |
|
âû- |
|||
|
¡ |
|
|
|
, получаем, что при |
|
|
||||||||
½2 |
|
(x |
|
x0)2 |
+ (y ¡ y0)2 |
< ±2; |
|
|
|
|
|
||||
|
|
|
± = min ±1; ±2 |
|
|
(x ¡ x0) + (y ¡ y0) |
|
< ± |
|
||||||
полняется jf(z) ¡fw0j ·gju(x; y) ¡ u0j + jv(x; yp) ¡ v0j < " ÷.ò.ä. |
|
|
|
||||||||||||
Замечание: Пределы в Теореме 3.1 должны браться именно по совокупности переменных. Это означает, что если предел limz!z0 f(z) = w0 ñóùå-
ствует, то он не зависит от способа приближения к точке z0
1
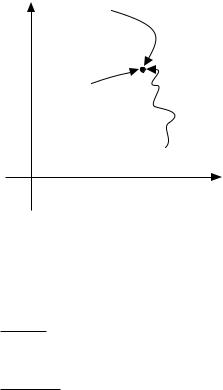
y |
z0=x0+iy0 |
|
x
Рис. 1: Пределы не зависят от способа приближения к z0 = x0 + iy0!
плоскости. Например, пределы по всем кривым, показанным на Рис. 2 равны. Аналогичное замечание справедливо в случаях z0 = 1 è w0 = 1.
Задача: Доказать утверждение, аналогичное Теореме 3.1 в случаях
(a) lim f(z) = |
1 |
; |
(b) lim f(z) = w |
0 |
|||
z |
! |
z0 |
|
z |
!1 |
||
|
|
|
|
|
|
||
Примеры:
(A) limz!1 z1 = 0. Действительно, каким бы ни было ", можно взять R = 1=", такое,то j1=zj = 1=jzj < " ïðè jzj > R.
(B) limz!0 e¡1=z2 не существует (в отличие от действительного случая!). Рассмотрим два способа приближения к пределу: (i) по действительной оси, справа и (ii) по мнимой оси, сверху. В случае (i) предел равен нулю (действительный случай). В случае (ii) сделаем замену z = iy и задача сведется
к вычислению предела limz!0 e1=y2 , который равен бесконечности. Таким образом, пределы по разным направлениям получаются разными и единого предела не существует.
Определение: Функция комплексной переменной f(z) называется непрерыв-
ной в точке z0 если существует ограниченный предел limz!z0 f(z) = w0 è
w0 = f(z0).
Определение (в терминах " ¡ ±): Функция комплексной переменной f(z)
называется непрерывной в точке z0 åñëè 8 > 0 9±(") > 0 такое, что при jz ¡ z0j± выполняется неравенство f(z) ¡ f(z0)j < ".
Определение: Функция комплексной переменной f(z) называется непрерывной в области G если она непрерывна в каждой точке z 2 g. Записывают
f(z) 2 C(G).
2
Теорема 3.2: Необходимым и достаточным условием непрерывности f(z) â G является требование, чтобы действительная и мнимая части f(z), u(x; y)
è v(x; y) были непрерывны в G по совокупности переменных. Доказательство: Следует непосредственно из Теоремы 3.1.
4. Дифференцирование функции комплексной переменной. Аналитические функции.
4.2. Производная комплексной функции. Условия Коши-Римана. Аналитические функции.
Определение: Однозначная функция f(z) 2 C(g) называется дифференциру-
емой в точке z = z0 åñëè ïðè z = z ¡ z0 ! 0 существует конечный предел отношения
lim |
f(z0 + |
z) ¡ f(z0) |
def= f0(z0): |
|
|||
|
z |
||
z!0 |
|
||
Теорема 4.1: (условия Коши-Римана в точке, необходимое условие). Если f(z) = u(x; y) + iu(x; y) дифференцируема в точке z0 = x0 + iy0, òî ñóùå-
ствуют частные производные ux(x0; y0); uy(x0; y0); vx(x0; y0); vy(x0; y0) и они связаны условиями Коши-Римана:
ux(x0; y0) = vy(x0; y0) uy(x0; y0) = ¡vx(x0; y0)
(1)
(2)
Доказательство: Воспользуемся тем, что в определении производной предел не зависит от способа приближения к точке z0.
(i) z = x ! 0 (приближение к точке z0 вдоль прямой, параллельной действительной оси)
f0(z0) = lim |
u(x0 + |
x; y0) + iv(x0 + x; y0) ¡ u(x0; y0) ¡ iv(x0; y0) |
= |
|
|||
|
x |
||
x!0 |
|
||
=ux(x0; y0) + ivx(x0; y0)
(ii)z = i y ! 0 (приближение к точке z0 вдоль прямой, параллельной
мнимой оси)
f0(z0) = lim |
u(x0; y0 + |
y) + iv(x0; y0 + |
y) ¡ u(x0; y0) ¡ iv(x0; y0) |
= |
|
|
|||
|
i |
y |
||
x!0 |
|
|||
= ¡iuy(x0; y0) + vy(x0; y0)
Следовательно, ux(x0; y0) = vy(x0; y0) è uy(x0; y0) = ¡vx(x0; y0) ч.т.д. Теорему 4.1 можно схематически изобразить в виде:
3

u(x; y),v(x; y) связаны усл. К-Р в z |
0 |
|
= |
f0 |
(z |
) |
|
|
|
||||||
|
|
( |
9 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Теорема 4.2: (условия Коши-Римана в точке, достаточное условие). Пусть f(z) = u(x; y) + iv(x; y). Если в точке z0 = x0 + iy0 существуют первые
дифференциалы функций u(x; y) è v(x; y) и первые частные производные
этих функций в точке (x0; y0) связаны условиями Коши-Римана (1)-(2), то f(z) - дифференцируемая функция в точке z0.
Доказательство: Òàê êàê u(x; y) è v(x; y) дифференцируемы в точке (x0; y0), то справедливы представления (см. курс действительного анализа)
u = ux(x0; y0)Δx + uy(x0; y0)Δy + »(x; y) v = vx(x0; y0)Δx + vy(x0; y0)Δy + ´(x; y)
ãäå |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и, следовательноp |
|
|
|
|
|
. |
|
p |
|
|
|
|
|
|
|
||
»(x; y) = o( x2 + y2) = o(jzj); ´(x; y) = o( |
|
x2 + y2) = o(jzj) |
|
||||||||||||||
|
|
³(x; y) ´ »(x; y) + i´(x; y) = o(jzj) |
|
Тогда, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
f(z0 + z) ¡ f(z0) |
= |
u + i v |
= |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
z |
z |
|
|
|
|
|
|
|
|
|
|
|||
= |
ux(x0; y0)Δx + uy(x0; y0)Δy + ivx(x0; y0)Δx + ivy(x0; y0)Δy |
+ |
³(x; y) |
= |
|||||||||||||
|
|
z |
|
||||||||||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
||
=[в силу условий ux(x0; y0) = vy(x0; y0) è uy(x0; y0) = ¡vx(x0; y0)]
=ux(x0; y0)Δx ¡ vx(x0; y0)Δy + ivx(x0; y0)Δx + iux(x0; y0)Δy + ³(x; y) = x + i y z
|
= ux(x0 |
; y0) + iv(x0; y0) + |
³(x; y) |
|
|
|
|
|
|
|
|
||
|
z |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
то есть существует предел |
|
|
|
|
|
|
|
||||||
|
lim |
f(z0 + |
z) ¡ f(z0) |
= f0(z0) = ux(x0; y0) + ivx(x0; y0) |
|
|
|
||||||
|
|
|
|
|
|||||||||
÷.ò.ä. |
z!0 |
z |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из Теоремы 4.2 следует другая схема: |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
1. |
u(x; y), v(x; y) диффер. функ. в z0 |
|
|
|
|
|
|
||||||
|
= |
f0 |
(z |
0 |
) |
|
|||||||
|
|
||||||||||||
|
|
||||||||||||
2. |
u(x; y), v(x; y) связаны усл. К-Р в z0 |
|
) |
9 |
|
|
|
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание: Производная может быть записана различными эквивалентными способами:
f0(z) = ux(x; y) + ivx(x; y) = vy(x; y) + ivx(x; y) =
= ux(x; y) ¡ iuy(x; y) = vy(x; y) ¡ iuy(x; y)
4
Замечание: Если функция дифференцируема в точке z0, то она и непрерыв- на в этой точке. Обратное, вообще говоря, неверно.
Определение: Функция f(z) называется аналитической в области G если она определена в области G, дифференцируема во всех точках z 2 G è f0(z) непрерывна в G.
Из Теорем 4.1 и 4.2 следует критерий аналитичности функции f(z) в области G:
Теорема 4.3: Необходимым и достаточным условиями аналитичности функции f(z) = u(x; y) + iv(x; y) в области G, являются непрерывность первых
частных производных ux, uy, vx, vy
Доказательство:
Необходимость: Из условия аналитичности f(z) следует, что f0(z) 2 C(G)
и, следовательно, ux; uy; vx; vy 2 C(G). Из Теоремы 4.1 следуют условия Коши-Римана.
Достаточность: Так как ux; uy; vx; vy 2 C(G), то существуют первые дифференциалы функций u(x; y), v(x; y). Следовательно, по Теореме 4.2 суще-
ствует f0(z) = ux + ivx. Ïðè ýòîì f0(z) непрерывна т.к. непрерывны ux è |
|||
vx. Теорема 4.3 доказана. |
|
|
|
Теорему 4.3 можно схематически изобразить в виде: |
|
||
1. |
ux; uy; vx; vy непрерывны в G |
() |
f(z) - |
2. |
u(x; y), v(x; y) связаны усл. К-Р в G |
аналитич. в G |
|
Замечание (для продвинутых") Оказывается, что0 в определении аналитической функции условие непрерывности производной f (z) 2 C(G) можно опустить. Ока-
зывается, что потребовав только условие0 дифференцируемости функции в области G, можно доказать, что условие f (z) 2 C(G) выполняется при этом авто-
матически. Но доказательство этого факта достаточно сложно. Приведем без доказательства критерий0 аналитичности функции, не требующий условия непрерывности производной f (z) 2 C(G):
Теорема 4.3¤:(для продвинутых , без доказательства) Необходимым и достаточ-
ным условиями аналитичности функции f(z) = u(x; y)+iv(x; y) в области G, являются непрерывность u(x; y), v(x; y) и существование в любой точке z = x + iy 2 G первых частных производных ux, uy, vx, vy, связанных условиями Коши-Римана.
Теорему 4.3¤ можно схематически изобразить так:
1. |
u(x; y), v(x; y) непрерывны в G |
|
|
|
|
f(z) - |
|
||
|
|
|||
|
|
|||
2. |
ux; uy; vx; vy существуют в G |
() |
|
|
аналитич. в G |
|
|||
3. |
u(x; y), v(x; y) связаны усл. К-Р в G |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
5

Пример: Рассмотрим функцию w = zz¯. Ее действительная часть u(x; y) = x2 + y2, мнимая часть v(x; y) = 0. Условия Коши-Римана имеют вид
2x = 0; 2y = 0
и удовлетворяются только в точке z = 0. По определению можно найти производную этой функции в точке z = 0:
w0(0; 0) = lim |
|
zΔ¯z |
|
= |
|
lim |
|
(Δx |
¡ |
i y) = 0 |
||
0 |
z |
x |
|
|||||||||
z |
! |
|
! |
0; y |
! |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
Однако эта функция не является аналитической ни в какой окрестности точки z = 0.
Теорема 4.4: (Условие Коши-Римана в полярных координатах) Пусть z =
½ei' = u(½; ') + iv(½; '). Тогда при z 6= 0 условия Коши-Римана (1)-(2) эквивалентны условиям
|
v' = ½u½ |
|
(3) |
||
|
u' = ¡½v½ |
|
(4) |
||
причем производная f0(z) выражается формулой |
|
||||
f0 |
|
i |
|
|
|
(z) = ¡ |
|
(u' |
¡ iv') |
(5) |
|
z |
|||||
Доказательство: Òàê êàê x = ½ cos ', y = ½ sin ', òî
u½ = ux cos ' + uy sin ';
u' = ¡ux½ sin ' + uy½ cos '; v½ = vx cos ' + vy sin '
v' = ¡vx½ sin ' + vy½ cos '
Используя условия Коши-Римана (1)-(2) имеем
u½ = vy cos ' ¡ vx sin ' = ½¡1v' u' = ¡vy½ sin ' ¡ v'½ sin ' = ¡½v½
Выражение для производной (5) получается если выразить частные производные ux, vx через u½, u', v½, v',
½ux = u½½ cos ' ¡ u' sin ' ½vx = v½½ cos ' ¡ v' sin '
и подставить в выражение для производной f0(z) = ux + ivx.
Примеры:
(A) Функция ez аналитическая. Для этого проверим условия КошиРимана
u(x; y) = ex cos y; v(x; y) = ex sin y
ux(x; y) = ex cos y = vy(x; y); uy(x; y) = ¡ex sin y = ¡vx(x; y)
6

(B)Функция zn, n 2 Z аналитическая. Проверим условия Коши-Римана
âполярных координатах
zn = ½n(cos n' + i sin n') v' = n ¢ ½n ¢ cos n' = ½u½ u' = ¡n ¢ ½n ¢ sin n' = ¡½v½
4.3. Свойства аналитических функций.
Свойство 1. Действительная и мнимая части аналитической функции удовлетворяют уравнению Лапласа
uxx + uyy = 0; vxx + vyy = 0
Доказательство: Дифференцируя первое условие условия Коши-Римана по x и второе по y имеем uxx = vyx è uyy = ¡vxy, следовательно uxx + uyy =
0. Дифференцируя первое условие условия Коши-Римана по y и второе по x аналогично получаем vxx + vyy = 0 ÷.ò.ä.
Функции, удовлетворяющие уравнению Лапласа называются гармони- ческими.
Свойство 2. Пусть f(z) è g(z) - однозначные аналитические функции в области G. Тогда
[a ] функция f(z) + g(z) является аналитической в G, причем
|
|
(f + g)0 = f0 + g0; |
(6) |
||||
[b ] функция f(z)g(z) является аналитической в G, причем |
|||||||
|
|
(fg)0 = f0g + g0f |
(7) |
||||
[c ] функция f(z) |
G всюду, где знаменатель |
||||||
|
|
|
|
g(z) является аналитической в |
|||
отличен от нуля, причем |
|
||||||
f |
|
0 |
= f0g ¡ fg0 |
|
|||
µ |
|
¶ |
|
|
|
|
(8) |
g |
|
|
g2 |
||||
Свойство 3. Пусть g(z) - однозначная аналитическая функция в области G, а функция f(z) определена и аналитична на подмножестве множества изменения g(z). Тогда функция f(g(z)) является аналитической в области G причем
(f(g(z))0 = f0[g(z)]g0(z) |
(9) |
Доказательство: (Свойств 2 и 3) Достаточно убедиться, что производные существуют и даются формулами (6)-(9). Доказательства формул (6)-(9) копируются с доказательств этих же формул для действительного случая,
7

так как обычные свойства алгебраических функций и предельного перехода сохраняются при переходе к функциям комплексного переменного. Проверим, например, формулу для производной произведения (7). Имеем
f(z + z)g(z + z) ¡ f(z)g(z) |
= |
|
z |
||
|
= |
f(z + z)g(z + z) ¡ f(z + z)g(z) + f(z)g(z + z) ¡ f(z)g(z) |
= |
||||||||
|
|
|
g(z + z) ¡ g(z) |
|
z |
|
f(z + z) ¡ f(z) |
|
|
|
= f(z + z) |
¢ |
|
+ g(z) |
¢ |
|
|||||
z |
z |
|||||||||
|
|
|
||||||||
Переходя к пределу при z ! 0 получаем формулу (7). Таким образом, в G существует производная функции f(z)g(z), определенная формулой (7), причем, в силу аналитичности f(z) è g(z) она непрерывна. Следовательно, f(z)g(z) аналитична в G. Дополнительно, в силу Теоремы 4.3, получаем,
÷òî äëÿ f(z)g(z) выполняются условия Коши-Римана. Остальные формулы (6), (7)-(9) доказываются аналогично.
Свойство 4. Пусть w = f(z) = f(x + iy) = u(x; y) + iv(x; y) - аналитическая функция в G è f0(z0) 6= 0, z0 = x0 + iy0 2 G. Тогда существует некоторая окрестность W точки w0 = u0 +iv0 = f(z0), в которой определена обратная функция z = Á(w), причем Á(w) является аналитической в W è
Á0(w) = 1=f0(z)
Доказательство: Функция f(z) сопоставляет паре чисел (x; y) пару чисел
(u(x; y); v(x; y)). Покажем, что в некоторой окрестности точки (u0; v0) по значениям (u; v) однозначно восстанавливаются значения x = x(u; v) è y =
y(u; v). Посчитаем якобиан отображения (x; y) ! (u; v) :
J(x; y) = |
¯ |
vx(x; y) vy(x; y) |
¯ |
= ux(x; y)vy(x; y) ¡ uy(x; y)vx(x; y) = |
|||||
|
¯ |
ux(x; y) uy(x; y) |
¯ |
|
|
|
|
|
|
|
¯ |
|
|
¯ |
|
|
|
|
|
= [óñë. Êîøè¯ |
-Римана] = u2 (x;¯ y) + v2 |
(x; y) = |
j |
f0 |
(z) 2 |
||||
|
|
|
x |
|
x |
|
|
j |
|
По условию, J(x0; y0) 6= 0. По теореме о неявной функции из действительного анализа имеется некоторая окрестность U точки (x0; y0), которая переводится функцией f(z) в некоторую окрестность W точки (u0; v0) ãäå
(a) существует однозначное обратное отображение (u; v) ! (x; y) èç W
âU;
(á)якобиан J(x; y) отображения (x; y) ! (u; v) не обращается в нуль при всех (x; y) 2 U.
Обозначим z = Á(w) комплексную функцию, переводящую u+iv â x+iy. Производная этой функции в точке w 2 W существует и равна
|
Á(w + w) Á(w) |
|
|
f(z + z) f(z) ¡1 |
1 |
||||
lim |
|
|
= lim |
µ |
|
¶ |
|
|
|
w ¡ |
z ¡ |
= f0(z) |
|||||||
w!0 |
z!0 |
||||||||
8
Эта производная непрерывна, так как f0(z) непрерывна и не обращается в нуль (так как не обращается в нуль якобиан), следовательно функция Á(w) является аналитической в W ÷.ò.ä.
Следствие (из свойств 2-4). Функции sin z,cos z, tg z, ctg z, sh z, ch z, th z, cth z являются аналитическими во всей расширенной комплексной плоскости. Функции Ln z, az, za, Arcsin z, Arccos z, Arctg z также являются анали-
тическими при правильном выборе значений этих многозначных функций и области задания.
Действительно, первые 8 функций получаются из функции ez ïðè ïî-
мощи операций сложения и суперпозиции и, следовательно, являются аналитическими. Последние 6 функций являются обратными к аналитическим и также являются аналитическими, если указать (а) ветвь"(т.е. значение многозначной функции, которое берется) и (б) область задания, в которой обратная функция определена однозначно.
Свойство 5. Пусть в односвязной области G плоскости (x; y) задана гармоническая функция u(x; y) и известно, что она является действительной
частью аналитической функции f(z). Тогда мнимая часть этой функции определяется с точностью до аддитивной постоянной.
90o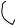




-1
|
1 |
t |
|
|
|
|
s |
|
|
n |
|
|
co |
|
z |
= |
|
e |
|
|
e |
|
|
R |
|
|
0.5 |
|
|
0.5 |
1 |
Im
z e
|
|
|
st |
|
|
n |
|
|
o |
|
|
= |
c |
|
|
|
|
|
|
 -0.5
-0.5
 -1
-1
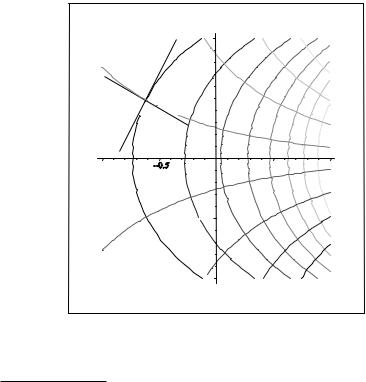
Рис. 2: Линии уровня действительной и мнимой частей функции w = ez.
Доказательство: Для восстановления мнимой части по известной функции u(x; y) определяем ее частные производные ux(x; y), uy(x; y). Из условий
9

Коши-Римана имеем производные мнимой части vx(x; y), vy(x; y), после чего мнимая часть находится путем интегрирования по x è y.
Аналогично, по мнимой части аналитической функции можно восстановить действительную.
Свойство 6. Линии уровня действительной и мнимой частей аналитической функции, u(x; y) = const è v(x; y) = const, ортогональны.
Доказательство: Ортогональность кривых линий определяется как ортогональность их нормалей в точке пересечения. Нормаль к линии уровня функции - это градиент функции. Тогда
grad u = (ux; uy); grad v = (vx; vy)
Скалярное произведение градиентов при этом рано нулю:
(grad u; grad v) = uxvx + uyvy = vyvx ¡ vxvy = 0
10
