

Лекция 1
1. Комплексные числа и последовательности комплексных чисел
1.1 Понятие комплексного числа.
Определение: Комплексным числом называется выражение вида x + iy, ãäå x è y - действительные числа, а i - символ, который называется мнимой единицей. Символ i отождествляется с корнем из ¡1:
i ¢ i = ¡1; |
(1) |
Числа x è y называются, соответственно, действительной и мнимой частями комплексного числа x + iy. При этом записывают:
x = Re(x + iy); y = Im(x + iy)
Действительные числа включаются в множество комплексных чисел. При этом полагается, что мнимая часть равна нулю. Те комплексные числа, у которых равна нулю действительная часть, называются чисто мнимыми1.
Два комплексных числа z1 = x1 + iy1 è z2 = x2 + iy2 считаются равными, z1 = z2, åñëè x1 = x2 è y1 = y2. Вместе с тем нельзя сказать, какое из двух
комплексных чисел z1 è z2 больше другого. Запись z1 > z2, åñëè ðå÷ü èäåò о комплексных числах - грубейшая ошибка(!)
Действия с комплексными числами: (введем формально)
Пусть z1 = x1 + iy1, z2 = x2 + iy2.
(A)Сложение: z1 + z2 = (x1 + x2) + i(y1 + y2)
(B)Вычитание: z1 ¡ z2 = (x1 ¡ x2) + i(y1 ¡ y2)
(C)Умножение: z1 ¢ z2 = (x1x2 ¡ y1y2) + i(x1y2 + y1x2)
Важно(!): комплексные числа можно умножать как многочлены, используя соотношение (1).
(D)Комплексное сопряжение: (обозначается z¯).
x + iy = x ¡ iy
1Историческая справка: Комплексные числа - сравнительно позднее изобретение че- ловечества. Формально, они появились в 16 веке в трудах Кардано (того самого, чьим именем называют формулу корней уравнения третьей степени), но он считал их бесполезными. Ньютон не считал комплексные числа "полноценными"числами, а Лейбниц считал их "убежищем божественного духа". В 18 веке комплексные числа стали чаще привлекать внимание исследователей. Символ i был предложен Леонардом Эйлером (1777). Систе-
матическое изложение теории комплексных чисел относится к концу 18-го - началу 19-го века.
1

Свойства:
(a) z1 § z2 = z¯1 § z¯2 (b) (¯z) = z
(c) z1 ¢ z2 = z¯1 ¢ z¯2
(d) z ¢ z¯ = (x + iy)(x ¡ iy) = x2 + y2 2 R
Полезные формулы:
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
Re z = |
|
|
|
(z + z¯) ; Im z = |
|
(z ¡ z¯) |
|
|
|
|
|
||||||||||
2 |
2i |
|
|
|
|
|
||||||||||||||||
|
(E) Деление: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
z1 |
= |
x1 + iy1 |
= |
|
(x1 + iy1)(x2 ¡ iy2) |
= |
x1x2 + y1y2 |
+ i |
y1x2 ¡ x1y2 |
|||||||||||
|
|
|
|
|
|
|
|
(x2 + iy2)(x2 ¡ iy2) |
x22 + y22 |
x22 + y22 |
||||||||||||
|
|
z2 |
x2 + iy2 |
|
|
|
|
|
||||||||||||||
|
Примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
(a) |
|
|
= ¡i |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
(b) |
|
|
|
2 + i |
|
= |
(2 + i)(1 ¡ 2i) |
= 0:8 |
¡ |
0:6i |
|
|
|||||||
|
|
|
1 + 2i |
|
|
|
||||||||||||||||
|
|
|
|
|
12 + 22 |
|
|
|
|
|
|
|
||||||||||
(F) Возведение в целую степень: Определим целую степень n комплексного числа z как произведение
zn = z ¢ z ¢ : : : z
| {z }
n ðàç
Таким образом возведение в целую степень сводится к многократно повторенной операции умножения.
Геометрическая интерпретация комплексных чисел.
Удобно ввести так называемую комплексную плоскость и ставить в соответствие точке плоскости с координатами (x; y) комплексное число x+iy.
При этом действительным числам будет соответствовать точки оси абсцисс, а мнимым - точки оси ординат. Перейдя на комплексной плоскости к полярным координатам, x = ½ cos ', y = ½ sin ', получим тригонометрическую
форму записи комплексного числа.
z = ½(cos ' + i sin ')
Ïðè ýòîìp
½ = x2 + y2 ´ jzj - модуль комплексного числа;
' - аргумент комплексного числа. Аргумент обозначается Arg z и определяется с точностью до любого слагаемого, кратного 2¼. В отличие от Arg z (бесконечно много значений) вводится еще arg z (главное значение
2

y
z=x+iy
ρ
ϕ
x
Рис. 1: Комплексная плоскость.
аргумента), соответствующее тому значению Arg z, которое лежит между ¡¼ è ¼. Очевидно, Arg z = arg z + 2¼k, k 2 Z. Справедлива формула
> |
arctg(y=x); x > 0; |
¸ |
|
> |
|
|
|
> |
¡ |
|
|
> |
|
y 0 |
|
8 |
¼ + arctg(y=x); x < 0; |
||
> |
¼=2; x = 0; y > 0 |
|
|
< |
y < 0 |
||
arg z = > |
|
¼ + arctg(y=x); x < 0; |
|
> |
¡ |
|
|
> |
|
|
|
> |
|
|
|
> |
|
|
|
> |
|
|
|
: |
|
¼=2; x = 0: y < 0 |
|
> |
|
|
|
Для комплексного числа 0 модуль равен нулю, а аргумент не определен.
Тригонометрическую и показательную форму записи комплексного числа связывает формула Эйлера
z = ½(cos ' + i sin ') = ½ei'
Эта формула является определением экспоненты в мнимой степени (ее не нужно доказывать).
Использование слова экспонента не случайно. Проверим для только что введенной экспоненты свойство, характерное для обычной экспоненты
ea+b = ea ¢ eb
Получим
ei'1 ¢ ei'2 = (cos '1 + i sin '1) ¢ (cos '2 + i sin '2) = [: : :] =
= (cos '1 cos '2 ¡ sin '1 sin '2) + i(sin '1 cos '2 + cos '1 sin '2) = ei('1+'2)
Примеры:
1. z = 1: j1j = 1, arg 1 = 0, 1 = 1 ¢ (cos 0 + i sin 0) = 1 ¢ ei¢0.
3
2. |
z = i: |
|
i |
= 1, arg i = ¼ |
i = 1 |
¢ |
(cos ¼ + i sin |
¼ ) = 1 |
¢ |
ei¢¼=2. |
|
|
|||||||||||||
|
|
|
|
j j |
|
|
|
2 , |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||
3. |
z = ¡1: j ¡ 1j = 1, arg (¡1) = ¼, ¡1 = 1 ¢ (cos ¼ + i sin ¼) = 1 ¢ ei¼. |
|
|||||||||||||||||||||||
4. |
z = |
|
i: |
j ¡ |
i |
j |
= 1, arg ( |
¡ |
i) = |
¼ |
i = 1 |
¢ |
(cos |
|
|
¼ |
+ i sin |
¼ |
) = |
||||||
1 ¢ e¡i¢¼=2. ¡ |
|
|
|
|
|
|
|
|
¡ 2 , |
¡ |
|
¡¡ 2 |
¢ |
¡¡ 2 |
¢ |
||||||||||
5. |
z = 1 + i: j1 + ij = p |
|
, |
arg (1 + i) = ¼4 , 1 + i = p |
|
¢ (cos ¼4 + i sin ¼4 ) = |
|||||||||||||||||||
2 |
2 |
||||||||||||||||||||||||
p |
|
¢ ei¢¼=4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. z = ¡ sin ¼8 ¡ i cos ¼8 : jzj = sin2 ¼8 + cos2 ¼8 = 1. Для нахождения аргумента отметим точку z на комплексной плоскости; она лежит на единичной
окружíости в третьей четверти.5ͼiетрудно сообразить, что ее аргумент равен ¡58¼ . Таким образом, z = e¡ 8 .
Геометрическая интерпретация действий с комплексными числами.
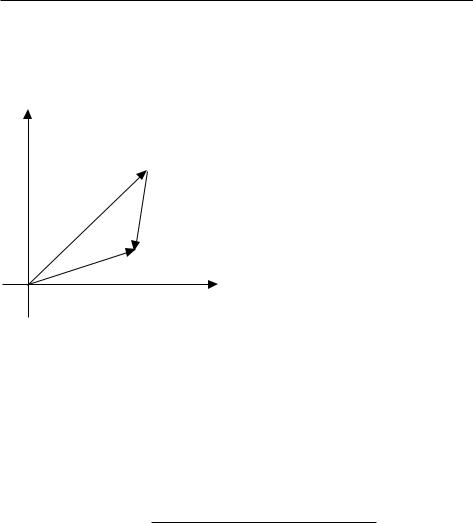
1. Сложение комплексных чисел можно рассматривать как сложение двух векторов на плоскости. Отсюда следует неравенство треугольника:
jz1 + z2j · jz1j + jz2j
y
z1
z2
z1+z 2
x
Рис. 2: Сложение комплексных чисел.
2. Умножение комплексных чисел. При умножении комплексных чисел их модули перемножаются, а аргументы складываются.
z1 ¢ z2 = ½1ei'1 ¢ ½2ei'2 = ½1(cos '1 + i sin '1) ¢ ½2(cos '2 + i sin '2) =
=½1½2f(cos '1 cos '2 ¡ sin '1 sin '2) + i(cos '1 sin '2 + sin '1 cos '2)g =
=½1½2fcos('1 + '2) + i sin('1 + '2)g = ½1½2ei('1+'2)
3.Деление комплексных чисел. При делении комплексных чисел их модули делятся, а аргументы вычитаются.
z1 |
= |
½1ei'1 |
= |
½1(cos '1 + i sin '1) ¢ (cos '2 ¡ i sin '2) |
= |
|
z2 |
½2ei'2 |
½2(cos2 '2 + sin2 '2) |
||||
|
|
|
4
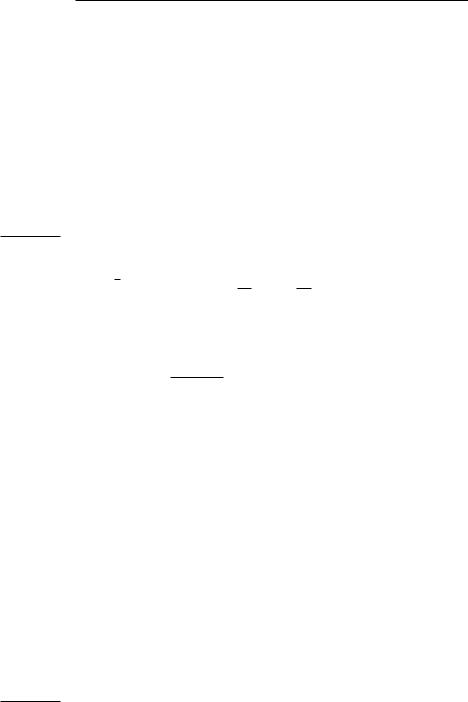
= |
½1f(cos '1 cos '2 + sin '1 sin '2) + i(¡ cos '1 sin '2 + sin '1 cos '2)g |
= |
||||||||||||
|
½1 |
|
|
|
|
|
|
½2 ¢ 1 |
½1 |
|
|
|||
= |
|
cos(' |
|
' |
) + i sin(' |
|
' ) |
|
= |
ei('1¡'2) |
||||
½2 f |
1 ¡ |
1 ¡ |
g |
½2 |
||||||||||
|
|
2 |
|
2 |
|
|
|
|||||||
4. Возведение в целую степень. Используем формулу Эйлера
zn = [½(cos ' + i sin ')]n = [исп. свойства умножения] = ½n(cos(n') + i sin(n'))
Тем самым мы вывели формулу Муавра
(cos ' + i sin ')n = cos(n') + i sin(n')
что эквивалентно
(ei')n = ein'
Примеры:
(A) Вычислить (1 + i)3
(1 + i)3 = ³p2ei¼=4´3 = 23=2 µcos 34¼ + i sin 34¼ ¶ = ¡2 + 2i
(B) Вычислить ³ |
|
1¡i |
|
|
´ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1+ip |
3 |
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 + ip |
|
|
40 |
|
|
|
|
|
|
|
2ei¼=3 |
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|||||||||||||||||||
|
à |
|
|
|
|
|
|
|
! |
|
= |
µ |
p |
|
e¡i¼=4 |
¶ |
|
= |
³p |
2 |
ei(¼=4+¼=3)´ |
= 220e70i¼=3 = |
|
|
|
|||||||||||||||||
|
|
1 ¡ i |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
20 |
e¡ |
2¼i=3 |
|
|
|
|
|
|
19 |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= 2 |
= |
|
|
|
2 |
|
|
|
3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
¡ |
|
|
(1 + i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(C) Решить уравнение zn¡1 = z¯, n |
2 |
Z, n = 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
2¼k |
|
|
|
|
|||
|
½n¡1ei(n¡1)' = ½e¡i' = |
|
|
½n¡2ein' |
= 1 = 1 |
¢ |
e2¼k = ½ = 1; |
' = |
; |
k |
2 |
Z |
||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
| |
|
|
|
{z |
|
|
|
|
|
|
} |
|
|
|
) |
| |
|
|
|
|
|
{z |
|
|
|
} |
) |
|
|
n |
|
|
|||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
øåì |
Извлечение целого корня (возведение в рациональную степень). Запи- |
|
|
|
||||||||||||||||||||||||||||||||||||||
zn = ½ei' = ½ei('+2¼k); k 2 Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
i('+2¼k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
z = ½n e |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|||||
Íî â ñèëó òîãî, ÷òî e2¼i = 1 формула (2) дает не бесконечное, а конечное число различных значений, соответствующих k = 0; 1; 2; : : : ; n ¡ 1. Таким образом, корень n-ой степени имеет n различных значений.
Примеры:
5

p
(A) Вычислить 4 1
|
|
|
|
|
|
|
|
|
|
1 |
ïðè |
k = 0; |
p4 |
|
= 1 |
|
ei(0+2¼k) 1=4 |
= |
8 i |
ïðè |
k = 1; |
||||
1 |
¢ |
|||||||||||
|
|
|
|
|
|
|
|
> |
1 |
ïðè |
k = 2; |
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
³ |
|
´ |
|
|
< |
¡ |
ïðè |
k = 3: |
|
(B) Вычислить |
|
|
|
|
> |
¡i |
|
|||||
|
|
|
|
|
5 |
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
p1 + i |
|
: |
|
|
|
||
5 |
|
|
|
|
|
|
|
|
|
i(¼=4+2¼k) |
´ |
1=5 |
10 |
|
|
i(¼=20+8¼k=20) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
p1 + i = ³p2 ¢¼e |
|
¼ |
|
|
= |
p2 ¢ e |
|
= |
|||||||||||||||
|
|
|
|
|
|
cos |
|
+ i sin |
|
|
|
|
|
ïðè |
k = 0; |
|
|||||||
|
|
|
|
|
|
20 |
20 |
|
|
|
|||||||||||||
|
|
|
|
|
8 cos |
920¼ + i sin 920¼ |
|
ïðè |
k = 1; |
|
|||||||||||||
|
10 |
|
|
|
> |
|
|
|
17¼ |
|
|
17¼ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
p2 |
|
> cos |
20 |
+ i sin |
|
20 |
ïðè |
k = 2; |
|
|||||||||||||
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
¢ |
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< cos |
25¼ |
+ i sin |
25¼ |
ïðè |
k = 3; |
|
||||||||||||
|
|
|
|
|
> |
|
|
|
20 |
|
|
20 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
33¼ |
+ i sin |
33¼ |
ïðè |
k = 4: |
|
||||||||||
|
|
|
|
|
> cos |
20 |
20 |
|
|||||||||||||||
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>
>
:
Простейшие множества точек на комплексной плоскости.
Выражение jz1 ¡ z2j представляет собой расстояние между точками на
комплексной плоскости, z1 è z2. Исходя из этого можно описать следующие множества:
(a) jz ¡ z0j = a, a > 0 - окружность с центром в точке z0 и радиусом a;
(b) jz ¡ z0j < a, a > 0 - открытый круг с центром в точке точке z0 è радиусом a;
(c) jz ¡ z0j ¸ a, a > 0 - внешность открытого круга с центром в точке точке z0 и радиусом a;
(d) a < jz ¡ z0j < b, 0 < a < b, - открытое кольцо с центром в точке z0;
Полезно также представлять себе следующие множества:
(e) arg(z ¡ z0) = ' - луч, с началом в точке z0, идущий под углом ' к положительному направлению действительной оси;
(f) ® < arg(z ¡ z0) < ¯, - внутренность неограниченного открытого сектора с вершиной в точке z0 и углом раствора ¯ ¡ ®;
(g) Re z = a - прямая, параллельная мнимой оси, проходящая через точку (a; 0);
(h) Im z = b - прямая, параллельная действительной оси, проходящая через точку (0; b).
1.2. Последовательности комплексных чисел
Определение: Последовательностью комплексных чисел называется упорядоченное счетное множество комплексных чисел fzng.
Определение: Комплексное число z называется пределом последовательно-
ñòè fzng åñëè 8" > 0 9N(") ÷òî 8n > N jz ¡ znj < ".
6

Записывают:
fzng ! z |
èëè nlim!1 zn = z |
|||
Примеры: |
|
|
|
|
(A) |
lim |
z0 |
= 0, z0 - любое комплексное число; |
|
|
||||
|
n!1 n |
|
||
(B) |
lim (cos 1±+i sin 1±)n не существует (необходимо проверить, что чле- |
|||
n!1
ны последовательности циклически повторяются, период равен 360).
Задание комплексной последовательности zn = xn + iyn соответствует одновременному заданию двух действительных последовательностей, fxng è fyng.
Теорема 1.1: Необходимым и достаточным условием того, что fzng ! z = x + iy является требование того, что fxng ! x è fyng ! y.
Доказательство:
Необходимость: 8" > 0 9N(") ÷òî jz¡znj < " 8n > N =) jxn¡xj · jzn¡zj < " è jyn ¡ yj · jzn ¡ zj < " =) fxng ! x è fyng ! y.
Достаточность: 8" > 0 9N1(") ÷òî jxn ¡xj < 2" 8n > N1 а также 9N2(") ÷òî jyn ¡ yj < 2" 8n > N2. Выбирая N = maxfN1; N2g, получаем, что jzn ¡ zj ·
jxn ¡ xj + jyn ¡ yj < " 8n > N ÷.ò.ä.
Теорема 1.2: (критерий Коши сходимости последовательности). Необходимым и достаточным условием сходимости fzng ! z является требование,
чтобы 8" > 0 9N(") äëÿ 8n > N è 8m > 0.
Доказательство:
Необходимость: Пусть zn = xn+iyn. Òàê êàê fzng ! z = x+iy, òî fxng ! x
è |
fyng ! y. Следовательно, по критерию Коши для действительных |
после- |
|||||||||||||
|
" |
|
|
||||||||||||
довательностей, |
8 |
" > 0 è |
m > 0 |
9 |
N1(") такое, что |
j |
xn+m |
¡ |
xn |
j |
< |
|
äëÿ |
||
|
|
|
8 |
|
|
|
|
2 |
|
" |
|||||
8n > N1("). Аналогично, 8" > 0 è 8m > 0 9N2(") такое, что jyn+m ¡ ynj < |
2 |
||||||||||||||
äëÿ 8n > N2("). Выбирая N(") = maxfN1; N2g имеем, что jzn+m ¡ zmj ·
jxn+m ¡ xnj + jyn+m ¡ ynj < " äëÿ 8n > N.
Достаточность: Из того, что jzn+m ¡ znj < " äëÿ 8n > N(") è 8m > 0
следует, что jxn+m ¡ xnj · jzn+m ¡ znj < " è jyn+m ¡ ynj · jzn+m ¡ znj < ".
Следовательно, последовательности fxng è fyng удовлетворяют условиям критерия Коши для действительных последовательностей и сходятся. По Теореме 1.1 последовательность fzng также сходится, ч.т.д.
Определение: Последовательность fzng называется ограниченной, если 9A 2 R ÷òî 8n jznj < A.
Определение: Если 8A > 0 9N(A) такой, что jznj > A äëÿ 8n > N(A), то такая последовательность называется неограниченно возрастающей.
7

Примеры:
(A) fzng = zn, jzj > 1 (модуль n-го члена равен jzjn - стремится к беско- нечности при n ! 1.)
(B) fzng = in
Задача: Привести пример последовательности, которая была бы неограни- ченной, но не являлась бы неограниченно возрастающей.
В обычном смысле неограниченно возрастающие последовательности не |
|||||
сходятся. Однако, оказывается удобным считать, что существует единствен- |
|||||
ная бесконечно удаленная точка и все неограниченно возрастающие после- |
|||||
довательности сходятся к ней. |
|
¢ |
|
|
|
Задача: Рассмотрим последовательность |
z |
n. Найти |
limn!1 jznj |
, |
|
limn!1 arg zn è limn!1 zn. |
zn = ¡1 + n |
|
|
||
8
