МОТС ИТМО

A( 1 x1 + 2 x 2)= 1 Ax1+ 2 A x 2= 1 y1+ 2 y2,

(2.25)

где 1 , 2 F ; x 1, x 2 X ; y1 , y2 Y ; y1 = A x1 ; y2 = A x2.

Ker{A}= N{A}={x X : A x =0}.

(2.27)

Определение 2.20 (О2.20). Рангом rang{A}=rank{A}=rA линейно-

го оператора A называется размерность dim Im{A}

образа Im{A}

этого оператора.

Определение 2.21 (О2.21). Дефектом def{A}= A

линейного опе-

ратора A называется размерность dim {Ker{A}=N{A}}

ядра (нуль–

пространства) этого оператора.

Определение 2.22 (О2.22). Подпространство X

линейного

пространства X называется инвариантным относительно линейного

оператора A, если выполняется условие

A ,

(2.28)

лучает представление

A ,

(2.29)

где «A » означает «A действует на вектор », « » означает «

умножить на »,

– скаляр, именуемый собственным значением

(числом) ЛО A,

–

собственный вектор ЛО A, линейная оболочка

Определение 2.24 (О2.24). Пусть в n мерном ЛП X Xn выбран

e e ;i

, а в

m мерном ЛП Y Ym

базис

1, n

выбран базис

i

линейного оператора

X ; y Y

A: X Y : y = Ax ; x

(2.30)

называется двумерный m n массив чисел, столбцовое представле-

ние которого

A [ A1 A2 ... An ] row{Ai ;i 1,n},

(2.31)

таково, что столбцы Ai i

его составлены из числовых коэффици-

1, n

ентов Aji j

;i

представления вектора A e в базисе f линей-

1, m

1, n

i

ной комбинацией

A ei A1i f1

A2i f2 ... Ami fm .

(2.32)

Примечание 2.8 (П2.8). Если вектор x

записать в координатной

n

форме в базисе e ei ;i

с помощью представления x xei ei , а

1,n

i 1

вектор y в координатной форме в базисе f

f j ; j

с помощью

1, m

m

представления y y fj f j

, то введение матрицы A линейного опера-

j 1

тора A позволяет от векторно-операторной формы (2.30) перейти к

векторно-матричной мультипликативной форме

y f Axe ,

(2.33)

в которой y f col y fj ; j

, xe col xei ;i

.

1, m

1, n

Определение 2.25 (О2.25). Две матрицы A и A называются по-

добными, если они задают один и тот же линейный оператор A относи-

тельно различных пар базисов e, f и

,

.

e

f

Примечание 2.9 (П2.9). В силу определения 2.25 линейному опе-

ратору A соответствует множество сколь угодной большой мощности

подобных матриц, каждая из которых порождается своей парой e, f

базисов.

Введем в рассмотрение матричное условие подобия двух матриц

одной размерности m n с помощью следующего утверждения.

Утверждение 2.2 (У2.2). Пусть линейный оператор A реализует

отображение A: X Y : y= Ax ; x X ; y Y : dim X n ;

dim Y m .Пусть

в ЛП X задана пара базисов e,

, каждый из которых представляет со-

e

бой

систему

линейно

независимых

векторов

соответстенно

e ei ;i

и

i ;i

.Базисы связаны матрицей M преобразо-

1,n

e

e

1, n

вания базисов, задаваемого соотношением

e M

e

,

(2.34)

где n n

M row Mi ;i

составлена из столбцов

матрица

1,n

M i ,

элементы которых M ji представляют собой коэффициенты ли-

нейного разложения элементов ei ;i

базиса e по базисным ком-

1,n

понентам e

i ;i

базиса

, задаваемого в форме

1, n

e

ei M1i

e

i M 2i

e

2 ... M ni

e

n .

(2.35)

Пусть в ЛП Y задана пара базисов

f ,

, которые составлены из

f

m векторов f fl ;l

и

f

l ;l 1, m соответственно и связаны

1, m

f

m m – матрицей T преобразования базисов в форме

f T

f

,

(2.36)

где матрица T строится по той же схеме, что и матрица M .

Тогда подобные m n матрицы

A и A , задающие линейный

оператор A относительно пар базисов

e, f и

,

соответственно

e

f

связаны матричным соотношением (условием) подобия

(2.37)

T

A

AM .

Доказательство утверждения строится на представлении беско-

динатных векторов x и

x , связанных в силу (2.34) векторно-

матричным соотношением

x M

x

,

(2.38)

векторно-матричным соотношением

y T

y

.

(2.39)

Если теперь векторно-операторное соотношение y= Ax

записать

в векторно-матричной форме, то для каждой пары базисов

e, f и

,

соответственно получим векторно-матричные представления

e

f

y Ax AM

x

,

(2.40)

y

Ax .

(2.41)

Подстановка (2.41) в (2.39) приводит к векторно-матричному со-

отношению

y T

Ax .

(2.42)

Сравнение векторно-матричных соотношений (2.40) и (2.42) при-

водит к соотношению (2.37).

■

Примечание 2.9 (П2.9). Так как матрицы преобразования базисов

M и T таковы, что существуют обратные им матрицы

M 1 и T 1 , то

(2.37) имеет следующие эквивалентные представления

A T

T 1 AM .

AM 1 ,

A

(2.43)

Примечание 2.10 (П2.10). Если размерности линейных про-

странств X и Y таковы, что они совпадают n m ,

базисы e,

и

e

M

AM, A M

M 1 AM,

A

AM 1 ,

A

(2.44)

где A и

– подобные n n квадратные матрицы.

A

A

(2.45)

или

A I 0 .

(2.46)

В (2.45), (2.46)

есть собственный вектор

ЛО A, записанный

имеет ненулевое решение 0 , если определитель этой системы ра-

вен нулю, т.е. при выполнении равенства

det A I 0

(2.47)

Уравнение (2.47) называется характеристическим уравнением

матрицы A (ЛО A), а его корни i ;i

являются собственными

1, n

значениями этой матрицы (ЛО

A ).

Пусть k – некоторое собственное значение матрицы A . Если ха-

рактеристический многочлен

можно представить в виде

Тогда собственный вектор k матрицы A ,

соответствующий значению

k , является решением уравнения

A k I k 0

(2.48)

Это означает, что вектор k принадлежит ядру матрицы A k I

т.е. k N A k I , таким образом, ядро

N A k I является собст-

образуют базис в пространстве X n , само пространство X n

расщепля-

ется оператором A с матрицей A в прямую сумму одномерных собст-

венных подпространств в форме

n

X n H k ; Hk N A k I ; k

1, n

.

(2.49)

k 1

Матрица A оператора A в базисе из собственных векторов являет-

ся диагональной с собственными значениями 1, 2 , ..., n

на главной

диагонали, при этом справедливо равенство

diag ;k

H 1 AH; H row H

;k

,

(2.50)

1,n

k

1,n

k

ния. Тогда

m1

m2 ... mk

и все собственные век-

1

1

1

подпространств:

Xn=K1 K2 … Kr.

(2.51)

J diag{J

, J

2

,...,J

r

} T 1 AT ,

(2.52)

1

где блоки Ji

имеют размерность mi mi и могут быть представле-

ны следующим образом:

Ji diag{Ji

, Ji ,...,Ji

}, причем каждый под-

1

2

i

блок имеет вид

i

1

0

0

0

1

0

J

i

;

(2.53)

ij

0, ....

....

0,

i

каждый блок Ti матрицы T [T1 T2 ,...,Tr ]

состоит из столбцов ко-

n

p 1 p

x

x

; p – целое положительное.

p

i

i 1

Наиболее употребительными векторными нормами являются нор-

мы при p 1, 2 и :

n

1.

x

1

xi

– абсолютная норма вектора;

i 1

2.

x

n

12

2

xi2

– квадратичная или евклидова норма вектора;

i 1

3.

x

lim

x

P

max

xi

– бесконечная или экстремальная норма

P

i 1,n

Приведенные векторные нормы эквивалентны в том смысле, что

для норм

x и

x

существуют положительные числа 1

и 2

такие,

что выполняются неравенства: 1 x

x

2 x .

Так для норм

x 1 ,

x 2 и

x выполняются оценочные неравенст-

ва:

x 2 x 1

n x 2 ,

x x 2

n x ,

x x 1

n x .

Линейное арифметическое пространств Xn с введенной векторной

нормой

x p образует линейное нормированное пространство, обозна-

чаемое в одной из форм X n ,

x p или X pn , в дальнейшем в основном

рассматривается случай p 2 , при этом индекс нормы опускается.

Примечание 2.11 (П2.11). Следует сказать, что норма позволяет

задавать

поверхности

постоянных

значений

нормы

в

форме

x p r const , которые представляют собой в зависимости от значе-

ния p индекса нормы сферы. Если размерность пространства n 2 , то

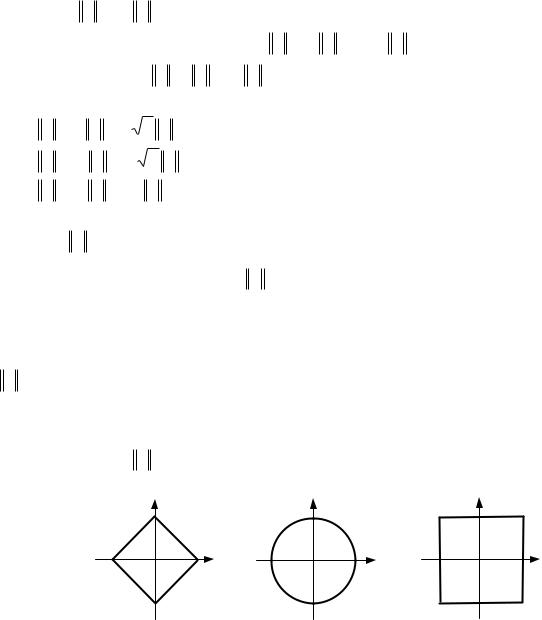
сферы становятся окружностями. На рисунках 2.1–2.3 приведены ок-

ружности вида

x p r

соответственно для p 1, 2, .

x2

x2

x2 r

x2

- x x

r

r x x

r

r

r

2

2

x1 r

1

1

-r

0

r

x1

-r

0

r x1

-r

0

r x1

- x1 r

- x1 x2 r

-r

x1 x2 r

-r

-r

x2 x2 r2

- x2 r

1

2

Рисунок 2.1

Рисунок 2.2

Рисунок 2.3

x, y x1 y1 x2 y2

n

n

... xn yn xi yi yi xi y, x .

(2.54)

i 1

i 1

Соотношения (2.54) делают справедливыми следующие представ-

ления скалярного произведения

x, y xT y yT x xT I y yT I x x, y

y, x .

(2.55)

I

I

Соотношения (2.55), содержащие представление

скалярного про-

изведения в виде

мультипликативной структуры «вектор–строка –

x, y

P

Px, y x, Py xT PT y xT Py.

(2.56)

Весовая матрица P должна быть: симметричной

P PT и поло-

вается ортогональной, если все векторы этой системы попарно ортого-

нальны:

ei ,e j 0;i, j

;i j .

1, n

ei ;i

векторов ЛП на-

Определение 2.33 (О2.33). Система

1, n

зывается

ортонормированной,

если

выполняется

равенство:

ei ,e j ij ;i, j

;

где символ Кронекера ij удовлетворяет условиям

1, n

ij

1 при i j и ij

0

при i j .

Определение 2.34 (О2.34). Евклидовым линейным пространством

E n

называется n мерное ЛП, в качестве базиса в котором использует-

ся система ei ;i

ортонормированных векторов таких, что матрица

1, n

E , имеющая своими столбцами вектора

ei ;i

, образует единич-

1, n

ную матрицу, т.е. выполняется матричное равенство

E row ei ;i

I .

1, n

(2.57)

Определение

2.35

(О2.35).

Базис,

построенный

на системе

v

e ; u

v1

;

1

1 1

v1

v e e ,u

u ; u

v2

;

2

2

2

2

1

1

v2

(2.58)

k 1

v e

(e ,u )u ;, u

k

vk

; k 2, n.

k

k

k

i i

vk

i1

В заключение раздела рассмотрим решение следующей задачи. В

ЛП Rn задан некоторый базис e ;i

относительно этого базиса

1,n

i

задан координатный вектор x col xi ;i

, задан

в ЛП и базис

1,n

fi ;i

, компоненты которого fi заданы в координатной форме от-

1, n

носительно того же базиса ei ;i

. Ставится задача конструирова-

1,n

ния представления вектора x относительно базиса fi ;i

в форме

1, n

n

x x f 1 f1 x f 2 f2 ... x fn fn x fi fi ,

(2.59)

i 1

так что относительно базиса fi ;i

вектор x

получает пред-

1, n

ставление

x f col x fi ;i

.

1, n

матричной форме имеет вид

col x

;i

Γ 1 ,

(2.61)

x

f

fi

1,n

где

Γ col row fi , f j ; j

;i

– матрица Грама, построен-

1,n

1,n

ная на скалярных произведениях всех пар элементов базиса fi ;i

1, n

друг на друга;

col x, fi ;i

– вектор–столбец из скалярных

1,n

произведений вектора x

на элементы базиса представления fi ;i

.

1, n

Следует заметить, что,

если базис

f состоит из ортонормированных