1.3. Монохроматичность, когерентность и поляризация света

Излучение может быть сосредоточено в одной или нескольких спектральных линиях, в полосах спектра конечной ширины или занимать относительно большой участок спектра. В соответствии с этим различают: линейчатый, полосатый и сплошной спектры.

1.3.1. Монохроматическое излучение

Ширину спектра источника света или линии излучения принято характеризовать степенью монохроматичности. В случае спектральной линии с длиной волны λ₀ степень монохроматичности можно выразить отношением:

,

где λ полуширина линии, λ₀ центральная длина волны.

Если λ/ λ₀ = 0, то излучение идеально монохроматично, а при λ/ λ₀ <<1 излучение называют квазимонохроматическим.

Высокой степенью монохроматичности обладает излучение газовых, твердотельных одночастотных полупроводниковых лазеров. Оно характеризуется одной частотой излучения и стабильностью начальной фазы.

Напряженность электрического поля одночастотного монохроматического излучения можно представить гармонической функцией

Е (t,z) = a₀ cos(₀ t + k z + ₀ ), (1.1)

где a₀ - амплитуда, ₀ - круговая частота, ₀ - начальная фаза, k=2n/ - волновое число, z - расстояние, t – время, n- относительный показатель преломления среды распространения волны.

Для монохроматического излучения начальная фаза сохраняется сколь угодно долго.

Из условий периодичности имеем:

,

отсюда

,

В вакууме n=1 и . Отсюда следует

.

Монохроматическое излучение с узкой шириной спектра и перестройкой частоты излучения получают с помощью монохроматора. Структурная схема монохроматора приведена на рис. 1.1.

Монохроматор работает следующим образом. Свет от источника излучения (лампы накаливания) 1 коллимируется линзой 2 в плоскопараллельный луч 3, падающий на отражательную дифракционную решетку 4 с поворотным механизмом 5. Дифракционная решетка отражает лучи разных длин волн под разными углами. Поворотный механизм позволяет плавно менять наклон решетки и, таким образом менять направление лучей разных длин волн 6 и 7. В результате луч 9, прошедший через выходную щель 8 монохроматора, является монохроматичным. Поворотом решетки монохроматор перестраивается на разные длины волн.

Рис. 1.1. Структурная схема монохроматора

1.3.2. Когерентность

Две волны называют когерентными, если разность их фаз остается постоянной. Когерентными являются две бесконечные (непрерывные) синусоидальные (монохроматические) волны с одинаковым периодом (частотой).

Основные понятия теории оптической когерентности можно рассмотреть на примере простых интерферометрических опытов. Схема эксперимента для наблюдения интерференции двух лучей от одного лазера приведена на рис 1.2.

Луч 2 лазера 1 подают на делительный кубик 3 , который делит луч на два луча, один из которых 5 является «прямо ходящим» или опорным. Другой луч 6 отражается от зеркала 4 и направляется на экран 7, где можно наблюдать интерференционную картину, состоящую из тёмных и светлых полос.

Качество видимости (резкость, четкость) интерференционных полос определяет степень когерентности излучения. Количественная оценка степени когерентности определяется коэффициентом видности из выражения:

, (1.2)

где J_макс интенсивность света в светлой полосе; J_мин интенсивность света в соседней, темной полосе.

Рис. 1.2. Схема получения интерференционной картины; (1 - лазер, 2 - луч лазера, 3 - делитель луча, 4 - зеркало, 5 и 6 - сравниваемые лучи, 7- экран для наблюдения интерференционной

картины

Если плавно перемещать зеркало 4 поступательно вниз, то на экране 7 можно увидеть перемещение светлых и тёмных полос. Этот эффект – интерференция используется в различных датчиках и измерителях интерференционного типа.

При анализе качества лазерного излучения используют понятия временной и пространственной когерентности. Принципы теории оптической когерентности аналогичны принципам волновой теории электромагнитных волн и соответствуют законам электродинамики. Здесь мы лишь отметим, что разделяют пространственной и временной когерентности.

Временная когерентность - это постоянство фазы волны в моменты времени, разделенные интервалами времени равными кратному числу периодов волны.

Пространственная когерентность - это постоянство фазы в пространстве в точках удаленных от источника излучения на расстояния кратные длине волны.

Когерентное излучение получают, в основном, с помощью лазеров различного вида:

– газовые лазеры имеют большие габариты, большие резонаторы, высокую степень монохроматичности и малую угловую расходимость; размеры газовых резонаторов L_рез = 1 … 10 [м];

– твердотельные лазеры также имеют большой резонатор и сохраняют фазу, их размеры L_рез 10 [см];

– полупроводниковые лазеры имеют малые размеры резонатора (L_рез 1 [мм]) и поэтому имеют довольно плохую когерентность и сильную угловую расходимость.

Реальные оптические пучки, создаваемые лазерами, не являются идеально когерентными. Проведем исследование интерференционной картины частично когерентных полей.

Если монохроматическую волну разделить в точке P, затем, собрать в точке Q (рис.1.3), то суммарное поле в ней будет:

, (1.3)

где t₁ и t₂ времена распространения до точки Q лучей 1 и 2.

Если величина скалярная (одна из компонент электрического поля) и является стационарным процессом (), то средняя по времени интенсивность в точкеQ будет:

, (1.4)

где и средние интенсивности лучей, а

Рис. 1.3. Формирование интерференционной картины

где и средние интенсивности лучей, акорреляционная функция волнового поля, определяемая выражением:

, (1.5)

где , аусреднение по интервалуT значительно большему периода колебаний.

Обычно удобней работать с нормированной корреляционной функцией:

. (1.6)

Она описывает когерентность второго порядка скалярного волнового поля E (t, z) и удовлетворяет неравенству:

.

Параметром когерентности второго порядка является видность (формула (1.2)).

Если , то можно ввести понятие корреляционной функции пространственной когерентности:

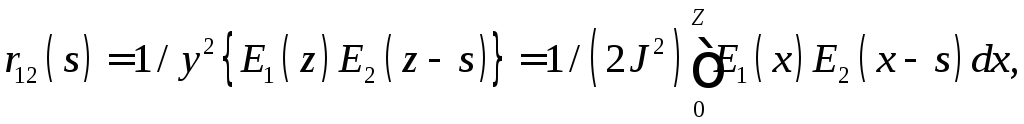(1.8)

где означает пространственное усреднение по интервалуZ.

Условие соответствует полностью пространственно когерентным волнам.

Это означает, что в точке Q интенсивность равна суммарной интенсивности двух монохроматических волн с частотой ω и разностью фаз:

,

где m целое число.

Если , то волны в противофазе и полностью некогерентны.иявляются мерами когерентности, при этом= 0,5 определяют как порог когерентности.

Величина , соответствующаяназывается интервалом временной когерентности. Для пространственной когерентности имеем, где интервал пространственной когерентности.

Для газовых лазеров и.

Для твердотельных лазеров и.

Для полупроводниковых лазеров и.

Модулированные оптические лучи некогерентны или квазикогерентны. Для них можно найти спектральную плотность через преобразование Фурье:

. (1.9)

Зная спектральную плотность, можно восстановить с помощью обратного преобразования Фурье:

. (1.10)

Ширина спектральной полосы , соответствует спектральной плотности

.

Как правило, выполняется условие:

.

В общем случае функция взаимной корреляции двух пучков света удовлетворяет пространственно-временному волновому уравнению:

, (1.11)

где – оператор Лапласа. Отсюда следует, что волны корреляции распространяются в пространстве.