
Программирование, вопросы / Лекц / Л_4_ИсслОп2012
.pdfФайл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА
ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
Лекция 4 Двойственность в линейном программировании
4.1 Понятие двойственности
Вспомним общую производственную задачу.
Рассмотрим деятельность некоторого производственного предприятия. Пусть наше предприятие может производить n видов продукции. Для их производства затрачивается m видов материальных ресурсов (сырье, денежные ресурсы, людские ресурсы и т.д.).
Технологией производства товара j назовем набор чисел
aij,i 1..m, j 1..n, показывающий, какое количество i-го ресурса необходимо
для производства единицы продукции j.
Получается технологическая матрица A=[aij], которая полностью описывает технологические потребности производства.
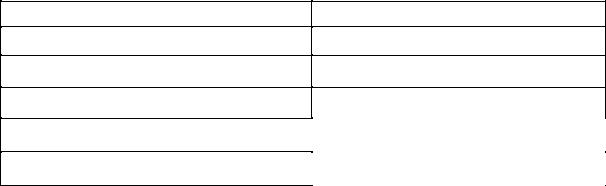
Пусть у нас имеется bi запасов i ресурса, и мы планируем произвести xj единиц j-ой продукции. Так как мы не можем выйти за пределы имеющихся у нас ресурсов, то наш план производства x (x1,x2,...,xn )должен
удовлетворять ограничениям
a11x1 a12x2 |
... a1nxn b1 |
|
|
|
a21x1 a22x2 |
... a2nxn b2 |
|
|
|
........................................... |
|
|
|
|
am1x1 am2x2 ... amnxn bm |
|
|
|
|
Ясно также, что x1 0,x2 |
0,...,xn 0. |
Так как мы стремимся иметь |
||
максимальную прибыль от нашего производства, получается такая задача |
||||
|
max n cj xj |
|
||
|
|
|
j 1 |
|
|
n |
aij xj bi ,i 1..m |
(1) |
|
|
j 1 |
|
|
|
xj 0, j 1..n
Наряду с этой задачей рассмотрим другую задачу, которая тесно связана с данной. Пусть y (y1,y2,...,ym ) - оценки ресурсов (“теневые”
цены). Тогда суммарная оценка всех ресурсов задается так:
y1b1 y2b2 ... ymbm . Мы будем ее минимизировать. При этом должны быть выполнены такие ограничения:
a11y1 a21y2 ... |
am1ym c1 |
a12 y1 a22 y2 ... |
am2 ym c2 |
......................................... |
|
a1n y1 a2n y2 ... |
amn ym cn. |
Итак, получается такая задача:
1
Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
m
min yibi
i 1
m |
|
aij yi cj , j 1..n |
(2) |
i 1
yi 0,i 1..m.
Задачи (1) и (2) называются парой двойственных задач. Свойство двойственности, очевидно, взаимно. То есть двойственной для задачи (2) будет задача (1).
Условия прямой задачи можно интерпретировать следующим образом. Коэффициент cj - прибыль, приходящаяся на единицу продукции j - го вида производственной деятельности. Расход ресурса i, запасы которого ограничены величиной bi, на единицу продукции j - го вида равен aij единицам этого ресурса.
Переменные двойственной задачи yi интерпретируются как внутренняя (теневая) цена единицы ресурса i (Поэтому их иногда называют теневыми ценами). Они могут быть использованы для определения приоритета используемых ресурсов в соответствии с их вкладом в величину целевой функции w, представляющую собой суммарную ценность ресурсов.
m
Сумму aij yi можно рассматривать как суммарную оценку всех
i 1
ресурсов j - го способа производства. Ограничения двойственной задачи можно интерпретировать следующим образом :
|
оценка всех ресурсовдля |
|
|
себестоимостьединицы |
|
|
|
|
|
продукции |
|
|
производстваединицыпродукции |
|
|
||
4.2 Различные формы прямой и двойственной задач. Принципы двойственности
Рассмотрим, как будет выглядеть пара двойственных задач в зависимости от формы задачи. Слева все векторы x, с, b – столбцы; справа все векторы у, с, b – строки; x, с – размерности n, y,b – размерности m.
maxcx |
|
minyb |
|
Ax b |
(1) |
yA c |
(2) |
x 0 |
|
y 0 |
|
mincx |
|
max yb |
|
Ax b |
(3) |
yA c |
(4) |
x 0 |
|
|
|
2
Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
maxcx |
|
min yb |
|
Ax b |
(5) |
yA c |
(6) |
x 0 |
|
|
|
mincx |
|
max yb |
|
Ax b |
(7) |
yA c |
(8) |
x 0 |
|
y 0 |
|
В общем случае пара двойственных задач определяется следующим образом:
Прямая задача
min c,x
ai,.,x bi , i=1…k
ai,.,x bi , i=k+1…m
xj 0, j=1…l
xj R1 , j=l+1…n
Двойственная задача
max y,b
yi R1 , i=1…k, т.е. без 0
yi 0, i=k+1…m
y,a., j cj , |
j=1…l |
y,a., j cj , |
j=l+1…n |
Как мы видим, действуют общие принципы формирования двойственной задачи ЛП. Приведем эти принципы:
1.Если исходная задача – задача на минимум, то двойственная задача – на максимум. И наоборот.
2.Столбец свободных членов прямой задачи становится коэффициентами целевой функции двойственной задачи.
3.Коэффициенты целевой функции прямой задачи становятся столбцом свободных членов ограничений двойственной задачи.
4.Матрица ограничений транспонируется.
5.Знак неравенства в задачах в стандартной форме меняется на противоположный.
6.Если в исходной задаче есть ограничения-равенства, то в двойственной задаче на соответствующие переменные не накладываются условия неотрицательности. И наоборот.
Теорема 4.1. Первая теорема двойственности. (док-во – см. Моп – теорема о седловой точке)
Для любой пары двойственных задач ЛП выполняется одна и только одна из следующих альтернатив:
1.Обе задачи имеют оптимальные решения, причем их оптимумы (значения целевых функций) совпадают.
2.Одна из задач имеет допустимые решения, а вторая не имеет. Тогда первая задача имеет неограниченную целевую функцию.
3.Ни одна из задач не имеет допустимых решений.
3

Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
4.3 Условия дополняющей нежесткости
Вначале рассмотрим условия дополняющей нежесткости в слабой форме для пары двойственных задач ЛП (1) и (2).
Теорема 4.2 (условия дополняющей нежесткости в слабой форме).
Пусть x и y - допустимые решения пары двойственных задач (1) и (2).
Для того, чтобы эти допустимые решения были оптимальными, необходимо и достаточно выполнение следующих условий:
|
|
|
|
|
|
y(b Ax) 0 |
(9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(yA c)x 0. |
|
|
Доказательство |
|
|||||
По условию теоремы |
x |
, |
y |
- допустимые решения (1) и (2): |
|
||
Ax b,x 0,yA c,y 0. Введем обозначения: |
|
||||||
y(b Ax) |
Очевидно, ≥ 0, ≥ 0. |
|
|||||
|
(yA c)x |
|
|||||
|
|
|
|
|
|
|
|
yb yAx yAx cx yb cx .
Необходимость. xи y - оптимальные решения (1) и (2) соответственно.
Тогда, по первой теореме двойственности, выполняется первая альтернатива, причем cx yb. Значит, 0. Но, т.к. ≥0, ≥0, то это возможно
лишь в случае, когда =0 и =0, а это и есть условия (13). Достаточность. Пусть выполнены условия (9). Но тогда 0. Откуда
следует, что cx yb. Если взять произвольное допустимое решение x, то Ax b, x 0, yAx yb cx . Аналогично, yAx cx. Отсюда cx cx. А так
как x было выбрано произвольно, это и означает, что x - оптимальное решение задачи (1).Аналогично доказывается, что y - оптимальное решение
задачи (2). Теорема доказана.
Замечание. Условия дополняющей нежесткости других пар двойственных задач будут отличаться от условий (9).
Запишем условия (9) в координатной форме.
m |
|
(b |
n |
|
x |
|
) 0 |
y |
a |
|
|
||||
i 1 |
i |
i |
j 1 |
ij |
|
j |
(10) |
n |
m |
|
|
|
|
||
|
|
|
|
|
)xj 0 |
||
( aij yi cj |
|||||||
j 1 |
i 1 |
|
|
|
|
|
|
Так как каждое слагаемое в этих суммах неотрицательно, то выполнение условий (10) возможно лишь в случае:
4
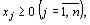
Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
y |
(b |
n a |
ij |
x |
j |
) 0, |
i 1..m |
|
|
i |
i |
j 1 |
|
|
(11) |
||
|
m |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
( aij yi cj )xj 0, |
j 1..n |
|||||||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
Отсюда следует, что если xj 0, то aij |
yi cj и, наоборот, |
|||||||
|
|
|
|
|
|
|
i 1 |
|
m |
|
|
|
|
|
|
|
n |
если aij yi cj , то xj 0 |
. Аналогично, если yi 0, то aij xj bi , и, |
|||||||
i 1 |
|
|
|
|
|
|
|
j 1 |
наоборот, если n aij xj bi , то yi 0. Отсюда и название - “условия
j 1
дополняющей нежесткости”.
4.4 Двойственный симплекс-метод.
Двойственный симплекс-метод, как иобычный симплекс-метод, используется при нахождении решенияпрямой задачи линейногопрограмммирования, записанной в форме основной задачи, для которой среди векторов Aj составленных из коэффициентов при неизвестных в системе уравнений, имеется m единичных. Вместе с тем двойственный симплекс– метод можно применять при решении задачи линейного программирования, свободные члены системы уравнений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными). Такую задачу и рассмотрим теперь, предварительно предположив, что (базисными) единичными являются векторы Aj j=1…m, т.е. рассмотрим задачу, состоящую в определении максимального значения функции
n сj xj F max |
(12) |
j 1 |
|
при условиях
n |
|
|
Aj xj A0 |
(13) |
|
j 1
(14)
и среди чисел 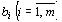 имеются отрицательные.
имеются отрицательные.
5
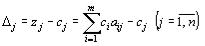
Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
В данном случае x = (b1, b2, …,bm, 0,…,0) есть решение системы линейных уравнений (13). Однако это решение не является планом задачи (12) – (14), так как среди его компонент имеются отрицательные числа.
Поскольку векторы Aj j=1…m – единичные, каждый из всех векторов Aj j=1…n можно представить в виде линейной комбинации данных m векторов, причем коэффициентами разложения всех векторов Aj по векторам Aj
j=1…m, служат числа 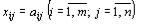 Таким образом, можно найти
Таким образом, можно найти
Определение.
Решение x = (b1, b2, …,bm, 0,…,0) системы линейных уравнений (13), определяемое базисом Aj j=1…m, называется псевдопланом задачи (12) –
(14), если i 0 для любого 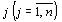
Теорема 4.3.
Если в псевдоплане x = (b1, b2, …,bm, 0,…,0), определяемом базисом Aj j=1…m, есть хотя бы одно отрицательное число bi< 0 такое, что вся i–ая
строка  , то задача (12) – (14) вообще не имеет планов.
, то задача (12) – (14) вообще не имеет планов.
Теорема 4.4.
Если в псевдоплане x = (b1, b2, …,bm, 0,…,0), определяемом базисом Aj j=1…m, имеются отрицательные числа bi< 0 такие, что для любого из них существуют числа aij<0, то можно перейти к новому псевдоплану, при котором значение целевой функции задачи (12) – (14) не уменьшится.
Теорема 4.5. При решении задачи двойственным симплекс-методом одновременно строится и оптимальный план другой (двойственной) задачи или устанавливается неограниченность снизу.
Сформулированные теоремы дают основание для построения алгоритма двойственного симплекс-метода.
Итак, продолжим рассмотрение задачи (12) – (14). Пусть x = (b1, b2, …,bm, 0,…,0) – псевдоплан этой задачи. На основе исходных данных составляют симплекс-таблицу, в которой некоторые элементы столбца вектора A0 являются отрицательными числами. Если таких чисел нет, то в симплекстаблице записан оптимальный план задачи (12) – (14), поскольку, по предположению, все i 0. Поэтому для определения оптимального плана задачи при условии, что он существует, следует произвести упорядоченный переход от одной симплекс–таблицы к другой до тех пор, пока из столбца
6
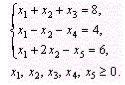
Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
вектора A0 не будут исключены отрицательные элементы. При этом все время должны оставаться неотрицательными все элементы (т +1)–й строки, т.е.
j 0 для любого 
Таким образом, после составления симплекс-таблицы проверяют, имеются ли в столбце вектора A0 отрицательные числа. Если их нет, то найден оптимальный план исходной задачи. Если же они имеются (что мы и предполагаем), то выбирают наибольшее по абсолютной величине отрицательное число. В том случае, когда таких чисел несколько, берут какое–нибудь одно из них: пусть это число bl. Выбор этого числа определяет вектор, исключаемый из базиса, т. е. в данном случае из базиса выводится вектор Al. Чтобы определить, какой вектор следует ввести в базис, находим
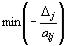 , где
, где  ( все i 0 ).
( все i 0 ).
Пусть это минимальное значение принимается при j=r, тогда в базис вводят вектор Ar. Число alr является разрешающим элементом. Переход к новой симплекс–таблице производят по обычным правилам симплексного метода. Итерационный процесс продолжают до тех пор, пока в столбце вектора A0 не будет больше отрицательных чисел. При этом находят оптимальный план исходной задачи, а следовательно, и двойственной. Если на некотором шаге окажется, что в i–ой строке симплекс–таблицы в столбце вектора A0 стоит отрицательное число bi, а среди остальных элементов этой строки нет отрицательных, то исходная задача не имеет решения.
Пример. |
|
|
|
|
|
|
|
F =x1 +x2 +2x3 |
|
Найти максимальное значение функции |
|
|
|
(15) |
|||||
при условиях |
|
|
|
|
|
|
|
|
|
x |
1 |
x |
2 |
x |
3 |
8 |
|
||
|
|
|
|
|
|
|
|||
|
|
x x |
|
4 |
|
||||
|
|
1 |
|
|
2 |
6 |
|
||
|
x1 2x2 |
|
|||||||
|
x1,x2,x3 0 |
|
|||||||
|
|
||||||||
Решение. Запишем исходную задачу линейного программирования в форме основной задачи: найти максимум функции (15) при условиях
7
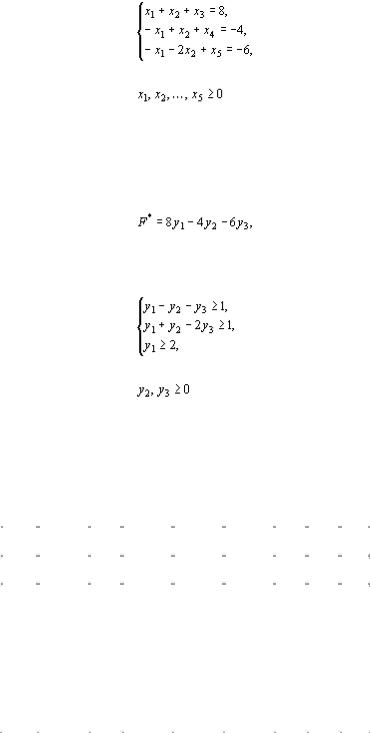
Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
Умножим второе и третье уравнения системы ограничений последней задачи на (–1) и перейдем к следующей задаче: найти максимум функции (15) при условиях
(16)
(17)
Составим для последней задачи двойственную задачу. Такой является задача, в результате решения которой требуется найти минимальное значение функции
(18)
при условиях
(19)
(20)
Выбрав в качестве базиса векторы A3, A4, A5, составим симплексную таблицу (табл. 1) для исходной задачи (15) – (16).
Таблица 1.
i |
Базис |
Сб |
A0 |
1 |
1 |
2 |
0 |
0 |
|
|
|||||||||
|
|
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
|
|
|
|
|||||
1 |
x3 |
2 |
8 |
1 |
1 |
1 |
0 |
0 |
|
|
|||||||||
2 |
x4 |
0 |
–4 |
–1 |
1 |
0 |
1 |
0 |
|
3 |
x5 |
0 |
–6 |
–1 |
–2 |
0 |
0 |
1 |
|
4 |
|
|
16 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Из этой таблицы видим, что планом двойственной задачи (57) – (59) является
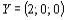 . При этом плане
. При этом плане 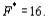 Так как в столбце вектора A0 таблица 1 имеются два отрицательных числа (–4 и –6), а в 4–й строке отрицательных чисел нет, то в соответствии с алгоритмом двойственного симплекс–метода переходим к новой симплекс–таблице. (В данном случае это можно сделать, так как в строках векторов A4 и A5 имеются отрицательные числа. Если бы
Так как в столбце вектора A0 таблица 1 имеются два отрицательных числа (–4 и –6), а в 4–й строке отрицательных чисел нет, то в соответствии с алгоритмом двойственного симплекс–метода переходим к новой симплекс–таблице. (В данном случае это можно сделать, так как в строках векторов A4 и A5 имеются отрицательные числа. Если бы
8

Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
они отсутствовали, то задача была бы неразрешима. Вектор, исключаемый из базиса, определяется наибольшим по абсолютной величине отрицательным числом, стоящим в столбце вектора A0. В данном случае это число (–6).
Следовательно, из базиса исключаем вектор A5. Чтобы определить, какой вектор необходимо ввести в базис, находим 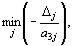 где
где 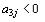 Имеем
Имеем
Значит, в базис вводим вектор A2. Переходим к новой симплекс–таблице 2:
Таблица 2.
|
i |
Базис |
Сб |
A0 |
1 |
1 |
2 |
0 |
0 |
|
|
|
|||||||||
|
|
|
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
|
|
|
|
|
|||||
|
1 |
x3 |
2 |
5 |
1/2 |
0 |
1 |
0 |
1/2 |
|
|
|
|||||||||
|
2 |
x4 |
0 |
–7 |
–3/2 |
0 |
0 |
1 |
1/2 |
|
|
3 |
x2 |
1 |
3 |
1/2 |
1 |
0 |
0 |
–1/2 |
|
|
4 |
|
|
13 |
1/2 |
0 |
0 |
0 |
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
Из этой таблицы видно, что получен новый план двойственной задачи
 При этом плане значение ее линейной формы равно F*=13. Таким образом, с помощью алгоритма двойственного симплекс–метода произведен упорядоченный переход от одного плана двойственной задачи к другому.
При этом плане значение ее линейной формы равно F*=13. Таким образом, с помощью алгоритма двойственного симплекс–метода произведен упорядоченный переход от одного плана двойственной задачи к другому.
Так как в столбце вектора A0 таблицы 2 стоит отрицательное число (–7), то рассмотрим элементы 2–й строки. Среди этих чисел есть одно отрицательное –3/2. Если бы такое число отсутствовало, то исходная задача была бы неразрешима. В данном случае переходим к новой симплекс-таблице 3.
Таблица 3.
i |
Базис |
Сб |
A0 |
1 |
1 |
2 |
0 |
0 |
|
|
|||||||||
|
|
|
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
|
|
|
|
|||||
1 |
x3 |
2 |
8/3 |
0 |
0 |
1 |
1/3 |
2/3 |
|
|
|||||||||
2 |
x1 |
1 |
14/3 |
1 |
0 |
0 |
–2/3 |
–1/3 |
|
|
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9

Файл Л_4_ИсслОп2012 = Л_6_ИслОп.doc из 3рус.doc ЧУВСТВИТЕЛЬНОСТЬ_ЗЛП.doc "прямая и двойственная задачи линейного программирования.mht" "Анализ решения задач оптимизации.doc" "Лекция 4-5.doc" "Двойственный симплекс-метод.doc" "ИССЛЕДОВАНИЕ МОДЕЛЕЙ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ.doc" ЧУВСТВИТЕЛЬНОСТЬ.doc
|
3 |
|
|
|
|
|
2/3 |
|
0 |
|
1 |
|
0 |
|
1/3 |
|
–1/3 |
|
4 32/3 0 0 0 1/3 2/3
Как видно из таблицы 3, найдены оптимальные планы исходной и двойственной задач. Ими являются X*=(14/3, 2/3, 8/3, 0, 0) и Y*=(2, 1/3, 2/3). При этих планах значения
линейных форм исходной и двойственной задач равны между собой: 
4.5 Экономическая интерпретация двойственной задачи
Для проведения содержательной интерпретации двойственной задачи (II) свяжем переменные двойственной задачи
Пусть L* - максимальное значение дохода в задаче (I). Если запасы ресурсов 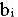 , i=1,...,m изменить, то может измениться и максимальный доход L*. Это означает, что L*
, i=1,...,m изменить, то может измениться и максимальный доход L*. Это означает, что L*
является функцией от ресурсов 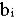 , i=1,...,m, т.е.
, i=1,...,m, т.е.
Рассмотрим отношение приращения дохода 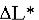 к приращению i-го ресурса
к приращению i-го ресурса
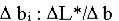 ;
;
Тогда по определению частной производной функции
Но по первой теореме двойственности оптимальное значение целевой функции прямой задачи совпадает с оптимальным значением целевой функции двойственной задачи
Таким образом, оптимальное значение двойственной переменной
числено равно дополнительномудоходу |
при увеличении i-го ресурса на единицу, |
если величина 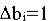 является достаточно малой по сравнению с величиной
является достаточно малой по сравнению с величиной 
10
