Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский национальный университет радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Л_6_ИсслОп2012

.pdf

Скачиваний:

Добавлен:

14.04.2015

Размер:

948.05 Кб

Скачать

☆

Л_6_ИсслОп2012.doc =~ Л_9_ИсслОп.doc из "Транспортная задача Л2.doc", "Транспортные задачи Л3-сокращен.doc", Зайченко:"Метод ПОТЕНЦИАЛОВ.doc" IASA-3_3.htm IASA-3_2.htm IASA-3_1.htm "АНАЛИЗ МЕТОДОВ РЕШЕНИЯ НЕЛИНЕЙНЫХ ТРАНСПОРТНЫХ ЗАДАЧ.doc"

Лекция 6 Метод ПОТЕНЦИАЛОВ

Метод потенциалов позволяет, исходя из некоторого опорного плана, построить за конечное число итераций решение Т-задачи.

Метод потенциалов впервые предложили Л.В. Канторович и М.К. Гавурин в 1949 г. Позже аналогичный метод разработал Г. Данциг, исходя из общих идей ЛП. Общая схема метода такова.

Вданном начальном опорном плане перевозок каждому пункту ставят

всоответствие некоторое число, называемое его предварительным потенциалом. Предварительные потенциалы выбирают так, чтобы их

разность для любой пары пунктов Ai и Bj, связанных основной коммуникацией, была равна cij. Если окажется, что разность (в другой форме записи – сумма) предварительных потенциалов для всех других коммуникаций не превосходит cij, то данный план перевозок - оптимальное решение задачи. В противном случае указывают способ улучшения текущего плана Т-задачи.

Как видно из решенного примера, алгоритм метода потенциалов следующий:

1)Занести данные задачи (транспортные издержки, спросы и предложения) в специальную рабочую таблицу;

2)Вычислить начальный опорный план (ОП);

3)Проверить ОП на оптимальность;

3.1) Найти значения потенциалов для данного ОП по формуле (21 Л5); если ОП вырожденный, то ввести фиктивные перевозки; 3.2) Проверить выполнение неравенств (22 Л5): если они все выполнены, то

данный ОП оптимален - вычисления прекратить; если нет, то перейти к пункту 4; 4) Построить новый ОП;

4.1) Построить цикл;

4.2) Изменить по вершинам цикла объемы перевозок; 4.3) Заполнить новую рабочую таблицу и перейти к пункту 3.

Приведем формальное описание алгоритма метода потенциалов.

Алгоритм складывается из предварительного этапа и конечного числа однотипных итераций. На предварительном этапе строят начальный

опорный план и составляют матрицу

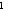
где

- предварительные потенциалы пунктов

Предварительный этап. С помощью известного метода (например северо-западного угла или минимального элемента) определяют начальный опорный план Х0 и вычисляют предварительные потенциалы

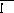
Вычисление предварительных потенциалов производят так. По найденному опорному плану Х0 строят схему перевозок Т-задачи из основных

коммуникаций плана. Напомним, что основные коммуникации 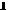плана Х0

- это те, которым отвечают базисные компоненты плана, т.е.

коммуникации для которых

. Далее образуют следующие множества:

- множество индексов всех пунктов Bj, которые связаны с пунктом А1

основными коммуникациями; І1 - множество индексов тех пунктов Аі,

которые связаны основными коммуникациями с множеством J1; J2 - множество пунктов Bj, которые связаны основными коммуникациями с множеством І1 и т.д. Образование таких множеств Ік продолжаем до тех пор, пока не получим пустое множество.

Поскольку на выполнение условий оптимальности оказывают влияние лишь

разности (см. теорему 2 прошлой Л5), то за начало отсчета (нуль) можно принять потенциал любого из пунктов.

Полагаем для определенности

и вычислим систему потенциалов

относительно А1. Тогда

где j

J1. Затем по значениям

определяем потенциалы пунктов

Аналогично вычисляем потенциалы (для и I1.) и т.д. После того как потенциалы всех пунктов найдены, строим матрицу

Очевидно, позиции матрицы С1, отвечающие базисным элементам плана Х0, будут заняты нулями. Если матрица С1 не содержит отрицательных элементов, то Х0 - оптимальный план. В противном случае Х0 - неоптимальный план, который может быть улучшен. Тогда переходим к выполнению однотипных итераций.

(k+1)-я итерация. Каждая итерация, кроме первой, где отсутствует первый этап, состоит из двух этапов. Предположим, что уже проведено k итераций (k=1,2,.), в результате которых получен план Хk и вспомогательная матрицу Сk. Цель (k+1)-й итерации - построение матрицы Сk+1, а также либо установление оптимальности плана Хk, либо нахождение более экономичного

плана Xk+1.

Первый этап. Вычисляют матрицу Сk+1. Преобразование матрицы Сk в матрицу Сk+1 состоит в следующем. Выбирают наибольший по модулю отрицательный элемент Сk. Пусть это элемент c (k)= k<0. Тогда

вычеркивают (или выделяют) строку , в которой он содержится. Просматривают эту строку и отыскивают множество существенных его

элементов. Хk -существенными элементами называют те элементы =0,

которые отвечают базисным элементам плана Хk т.е. для которых . Вычеркивают столбцы, которые содержат эти элементы. Далее просматривают вычеркнутые столбцы и ищут в них новые существенные элементы, которые лежат в строках отличных от уже вычеркнутых ранее. Если такие элементы имеются, то вычеркивают строки, в которых они

содержатся. Процесс выделения продолжают до тех пор, пока очередное множество новых существенных элементов не окажется пустым. Поскольку каждые строка и столбец не могут быть выделены дважды, то весь процесс заканчивается не более чем за l =m+ n - 1 шагов. Далее строят матрицу Сk+1.

Для этого величину прибавляют ко всем элементам выделенных строк и вычитают из элементов всех выделенных столбцов матрицы Сk. При этом все существенные элементы матрицы Сk остаются равными нулю, а кроме того, в нуль превращается и элемент c .

Если все элементы матрицы Сk+1 окажутся неотрицательными, то Xk - оптимальный план, и на этом процесс заканчивается. В противном случае переходят ко второму этапу.

Второй этап. Цель этого этапа - построить более экономичный план Хk+1. Выбирают наибольший по модулю отрицательный элемент матрицы

Сk+1. Пусть это элемент . Строят цепочку из положительных

элементов плана, которая замыкается на . После того, как цепочка построена, в ней находят минимальный нечетный по порядку следования элемент:

Прибавляют ко всем четным элементам (по порядку следования) цепочки

и к элементу и вычитают из всех нечетных элементов. Остальные элементы Хk оставляют без изменения. Новый план Хk+1 построен. Он является базисным, так как число его ненулевых элементов не изменилось.

Пусть Lk - транспортные издержки, отвечающие плану Хk. Тогда новое значение целевой функции, отвечающее плану Xk+1, находят по соотношению

				.	(1)
			. Поэтому Хk+1	.	(1)
Так как	и	, то		- улучшенный опорный



план. Затем производят аналогично (k+2)-ю итерацию, и т.д..

Примечания к методу потенциалов.

1.Систему потенциалов однозначно можно вычислить только для невырожденного ОП, при этом одному из потенциалов нужно придать

произвольное значение (обычно u1=0, т.к. в системе ограничений закрытой ТЗ имеется одно линейно зависимое ограничение).

2.В случае вырожденного ОП нужно ввести фиктивные перевозки с таким расчетом, чтобы из системы (12 Л5) однозначно вычислить все потенциалы.

3.Цикл всегда существует и единственен для каждой свободной клетки таблицы (для невырожденного ОП).

4.Если для какой-то свободной клетки (xij= 0) оптимального ОП в соотношении (13 Л5) достигается строгое равенство, то это говорит о неединственности оптимального ОП.

В зависимости от содержательной трактовки чисел сij транспортная задача может быть поставлена на минимизацию суммарного расстояния или

времени Пробега транспорта или на минимизацию расхода горючего, более общей является открытая модель ТЗ (когда не требуется выполнения равенства (11 Л5)) и сетевая постановка ТЗ (когда один и тот же пункт выступает в роди производителя и потребителя),. Открытые ТЗ решаются путем сведения к замкнутой ТЗ (вводятся фиктивные потребители или производители), а для решения сетевых ТЗ существуют специальные методы (например, метод динамического программирования).

Связь метода потенциалов с симплекс - методом

Пусть - некоторый базисный план Т-задачи. Множество, состоящее из базисных векторов Pij этого плана, которые отвечают его основным коммуникациям, обозначим через Kx. Напомним, что Kx состоит из (m + n - 1) векторов.

На первом этапе метода потенциалов вычисляют предварительные

потенциалы

, которые удовлетворяют условиям

. Величина имеет смысл симплекс – разности (в

прежних обозначениях или ). Предположим, что для всех Pij Kx. Это означает, что при введении в базис любого из таких векторов Pij уменьшить значения L(Xk) нельзя, а поэтому план Xk - оптимальный. Если же

для некоторого вектора 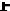величина , то при введении этого вектора в базис можно уменьшить значение целевой функции L(Х).

Переход к новому базису, который включает вектор 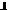, связан с

построением цепочки, которая замыкается на элементе . Чтобы

определить, какой вектор выводится из базиса, разлагают 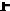по векторам старого базиса. Далее отыскивают

(2)

где - базисный элемент плана Хk при векторе 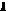, выводимом из базиса;

- коэффициент разложения вектора при векторе .

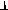
Для Т-задачи всегда . При этом , если элемент занимает

нечетную позицию в цепочке, которая замыкается на элементе , и , если он занимает четную позицию. Новые базисные значения переменных в общем случае симплекс-метода определяется по формуле

(3)

Поскольку , формулы (2) и (3) применительно к Т-задаче можно представить следующим правилом:

перевозки, запланированные по нечетным (четным) позициям цепочки, уменьшаются (увеличиваются) на величину ;

перевозка между

, а остальные перевозки сохраняют

свои значения (где - минимальный нечетный по порядку следования

элемент цепочки, которая соединяет пункты и ).

Таким образом, метод потенциалов является частным случаем симплекс-метода, учитывающим специфику Т-задачи.

Решение транспортной задачи при вырожденном опорном плане

Опорный план называется вырожденным, если число его ненулевых перевозок k меньше ранга матрицы ограничений. В процессе построения начального плана или при его улучшении очередной план может оказаться вырожденным.

Рассмотрим два случая.

1. Вырожденный план является начальным Х0 . Тогда выбирают некоторые нулевые элементы матрицы Х0 в качестве базисных так, чтобы при этом не нарушалось условие базисного плана. Число этих элементов равняется

. Далее данные элементы заменяют на (где - произвольное, бесконечно малое число) и рассматривают их как обычные базисные элементы плана. Задачу решают как невырожденную, а в последнем оптимальном плане Хk вместо пишут нули.

2. Вырожденный план получается при построении плана Хk+1 на базе Хk, если цепочка в плане Хk содержит не менее двух минимальных нечетных элементов. В таком случае в матрице Хk+1 полагают равным нулю только один из этих элементов, а остальные заменяют на , и далее решают задачу

как невырожденную. Если на k-м шаге , то при переходе от Хk к Хk+1

значение целевой функции не изменяется, а в базис вводится элемент , для которого перевозка станет равной .

Венгерский метод

Идея метода была высказана венгерским математиком Эгервари и состоит в следующем. Строится начальный план перевозок, не удовлетворяющий в общем случае всем условиям задачи (из некоторых пунктов производства не весь продукт вывозится, потребность части пунктов потребления не полностью удовлетворена). Далее осуществляется переход к новому плану, более близкому к оптимальному. Последовательное применение этого приема за конечное число итераций приводит к решению задачи.

Алгоритм венгерского метода состоит из подготовительного этапа и из конечного числа итераций. На подготовительном этапе строится матрица X0 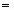(xij[0])m,n, элементы которой неотрицательны и удовлетворяют неравенствам:

,	i 1, …, m;
,	j 1, …, n.

Если эти условия являются равенствами, то матрица Хo - решение транспортной задачи. Если среди условий имеются неравенства, то осуществляется переход к первой итерации. На k-й итерации строится матрица Хk 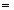(xij[0])m,n. Близость этой матрицы к решению задачи характеризует число k — суммарная невязка матрицы Хk:

В результате первой итерации строится матрица Хl, состоящая из неотрицательных элементов. При этом l 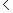0. Если l 0, то Хl - оптимальное решение задачи. Если l 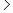0, то переходят к следующей итерации. Они проводятся до тех пор, пока k при некотором k не станет равным нулю. Соответствующая матрица Хk является решением транспортной задачи. Венгерский метод наиболее эффективен при решении транспортных задач с целочисленными объемами производства и потребления. В этом случае число итераций не превышает величины 0/2, где 0 - суммарная невязка подготовительного этапа. Достоинством венгерского метода является возможность оценивать близость результата каждой из итераций к оптимальному плану перевозок. Это позволяет контролировать процесс вычислений и прекратить его при достижении определенных точностных показателей. Данное свойство существенно для задач большой размерности.

Рассмотрим основные идеи венгерского метода на примере решения задачи выбора (задачи о назначениях), которая является частным случаем Т- задачи с булевой матрицей Х. Для общего случая также существует модификация венгерского метода (см., например, учебник Зайченко).

Задача о назначениях

Пусть имеется m неделимых ресурсов Ai, i=1,2,…,m, назначаемых только один раз, и n объектов Bi, i=1,2,…,n потребителей ресурсов, каждый из которых может потребить только один ресурс. Обозначим cij - затраты , связанные с назначением ресурса i на объект j. Задача состоит в определении такого плана назначения, при котором суммарная стоимость назначения

минимальна.
	Примеры задач приведены в таблице :
	Ресурсы	объекты	критерий
	Рабочие	Места работы	Время / зарплата
	Автобусы	маршруты	Затраты или объём
	Автобусы	маршруты	перевозок
			перевозок

Определим переменную xij {0,1} причем xij = 1, если ресурс i назначен на объект j, и xij = 0, если отсутствует назначение ресурса i на объект j. Тогда задача состоит в минимизации целевой функции стоимости назначений

m n

cij xij min i 1 j 1

при ограничениях первой группы, задающих использование каждого ресурса ровно 1 раз.

n xij 1, i 1,2, ,m.

j 1

Вторая группа ограничений гарантирует объекту использование одного ресурса

m
xij 1,	j 1,2, ,n.
i 1

Задача о назначениях - это пример целочисленной задачи линейного программирования. Она решается следующим специальным методом, хотя может быть решена методом потенциалов или симплекс-методом.

Венгерский метод для задачи о назначениях

Введем следующие понятия.

Нулевые элементы

матрицы С называются независимыми

нулями, если для любого

строка и столбец, на пересечении которых

расположен элемент , не содержат другие такие элементы .

Две прямоугольные матрицы С и D называются эквивалентными (C ~ D)

сточки зрения назначений, если для всех i,j . Задачи о назначениях, определяемые эквивалентными матрицами, являются эквивалентными (т.е. оптимальные решения одной из них будут оптимальными и для второй, и наоборот).

Описание алгоритма венгерского метода

Алгоритм состоит из предварительного этапа и не более чем (n-2) последовательно проводимых итераций. Каждая итерация связана с эквивалентными преобразованиями матрицы, полученной в результате проведения предыдущей итерации, и с выбором максимального числа независимых нулей. Окончательным результатом итерации является увеличение числа независимых нулей на единицу. Как только количество независимых нулей станет равным n, проблему выбора оказывается решенной, а оптимальный вариант назначений определяется позициями независимых нулей в последней матрице.

Предварительный этап. Разыскивают максимальный элемент в j - м столбце и все элементы этого столбца последовательно вычитают из максимального. Эту операцию проделывают над всеми столбцами матрицы

С. В результате образуется матрица с неотрицательными элементами, в каждом столбце которой имеется, по крайней мере, один нуль.

Далее рассматривают i - ю строку полученной матрицы, разыскивают ее минимальный элемент ai и из каждого элемента этой строки вычитают минимальный. Эту процедуру повторяют со всеми строками. В результате получим матрицу С0 (С0 ~ C), в каждой строке и столбце которой имеется, по крайней мере, один нуль. Описанный процесс преобразования С в С0 называется приведением матрицы.

Находим произвольный нуль в первом столбце и отмечаем его звездочкой. Затем просматриваем второй столбец, и если в нем есть нуль, расположенный в строке, где нет нуля со звездочкой, то отмечаем его звездочкой. Аналогично просматриваем один за другим все столбцы матрицы С0 и отмечаем, если возможно, следующие нули знаком '*'. Очевидно, что нули матрицы С0, отмеченные звездочкой, являются независимыми. На этом предварительный этап заканчивается.

(k+1)-ая итерация. Допустим, что k-я итерация уже проведена и в результате получена матрица Сk. Если в ней имеется ровно n нулей со звездочкой, то процесс решения заканчивается. В противном случае переходим к (k+1) - й итерации.

Каждая итерация начинается первым и заканчивается вторым этапом. Между ними может несколько раз проводиться пара этапов: третий - первый. Перед началом итерации знаком '+' выделяют столбцы матрицы Сk, которые содержат нули со звездочками.

Первый этап. Просматривают невыделенные столбцы Сk. Если среди них не окажется нулевых элементов, то переходят к третьему этапу. Если же невыделенный нуль матрицы Сk обнаружен, то возможен один из двух случаев:

1)строка, содержащая невыделенный нуль, содержит также и нуль со звездочкой;

2)эта строка не содержит нуля со звездочкой.

Во втором случае переходим сразу ко второму этапу, отметив этот нуль штрихом.

В первом случае этот невыделенный нуль отмечают штрихом и выделяют строку, в которой он содержится (знаком '+' справа от строки). Просматривают эту строку, находят нуль со звездочкой и уничтожают знак '+' выделения столбца, в котором содержится данный нуль.

Далеепросматриваютэтотстолбец(которыйуже сталневыделенным)и отыскиваютвнем невыделенныйнуль(илинули),вкоторомоннаходится. Этотнульотмечают штрихомивыделяютстроку,содержащуютакойнуль(или нули).Затем просматриваютэтустроку,отыскиваявнейнульсо звездочкой. Этот процесс за конечное число шагов заканчивается одним из следующих исходов:

1) все нули матрицы Сk выделены, т.е. находятся в выделенных строках или столбцах. При этом переходят к третьему этапу;

2) имеется такой невыделенный нуль в строке, где нет нуля со звездочкой. Тогдапереходятковторомуэтапу,отметивэтотнульштрихом.

Второй этап. На этом этапе строят следующую цепочку из нулей матрицы Сk: исходный нуль со штрихом, нуль со звездочкой, расположенный в одном столбце с первым нулем со штрихом в одной строке с предшествующим нулем со звездочкой и т.д. Итак, цепочка образуется передвижением от 0' к 0* по столбцу, от 0* к 0' по строке и т.д.

Можно доказать, что описанный алгоритм построения цепочки однозначен и конечен, при этом цепочка всегда начинается и заканчивается нулем со штрихом.

Далее над элементами цепочки, стоящими на нечетных местах ( 0' ) -, ставим звездочки, уничтожая их над четными элементами ( 0* ). Затем уничтожаем все штрихи над элементами Сk и знаки выделения '+'. Количество независимых нулей будет увеличено на единицу. На этом (k+1) - я итерация закончена.

Третий этап. К этому этапу переходят после первого, если все нули матрицы Сk выделены. В таком случае среди невыделенных элементов Сk выбирают минимальный и обозначают его h (h>0). Далее вычитают h из всех элементов матрицы Сk, расположенных в невыделенных строках и прибавляют ко всем элементам, расположенным в выделенных столбцах. В результате получают новую матрицу С'k, эквивалентную Сk. Заметим, что при таком преобразовании,всенулисо звездочкойматрицыСk остаются нулямии вС'k,крометого,вней появляютсяновые невыделенныенули. Поэтомупереходятвновькпервомуэтапу.Завершивпервый этап,в зависимостиотегорезультата либопереходят ко второму этапу, либо вновь возвращаются к третьему этапу.

После конечного числа повторений очередной первый этап обязательно закончится переходом на второй этап. После его выполнения количество независимых нулей увеличится на единицу и (k+1) - я итерация будет закончена.

Соседние файлы в папке Лекц

#
14.04.2015370.24 Кб18Л_1_ИсслОп.pdf
#
14.04.2015223.5 Кб18Л_2_ИсслОп2012.pdf
#
14.04.2015311.56 Кб18Л_3_ИсслОп2012.pdf
#
14.04.2015273.6 Кб20Л_4_ИсслОп2012.pdf
#
14.04.20151.89 Mб17Л_5_ИсслОп2012.pdf
#
14.04.2015948.05 Кб19Л_6_ИсслОп2012.pdf
#
14.04.2015320.17 Кб18Л_7_ИсслОп.pdf
#
14.04.2015226.24 Кб18Л_8_ИсслОп.pdf
#
14.04.20151.77 Mб20Л_9_ИсслОп.pdf
#
14.04.2015254.48 Кб19Лекция14 ОптУпр.pdf
#
14.04.2015238.85 Кб23Модели управления запасами_Л1.pdf