Программирование, вопросы / Лекц / Л_1_ИсслОп

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

Лекция 1 ( из 17 – все в одном семестре) ВВЕДЕНИЕ В ПРЕДМЕТ

Литература, необходимая для изучения курса

1. Вагнер Г. Основы исследования операций. Т. 1-3. М.: Мир, 1972 2. Зайченко Ю.П. Исследование операций. – Киев: Вища школа, 1979. – 320с.

3. Акулич И.Л. Математическое программирование в упражнениях и задачах.

– М. : Высшая школа, 1985. – 285с.

4.Кузнецов В.А., Сакович И.Н., Холод И.В. Высшая математика. Математическое программирование. – Мн. : Вышейша школа, 1985. – 392с.

5.Вентцель Е.С. Исследование операций. – М.: Сов.радио, 1972. – 552с.

6.Петросян Л.А., Данилов Н.Н. Кооперативные дифференциальные игры и их приложения. – Томск: Изд-во томского ун-та, 1985. – 276с.

Электронные ресурсы ( возможны изменения ) http://kpmit.wl.dvgu.ru/library/aschepkov_oper_research_elements http://math.nsc.ru/LBRT/k5/mo.html http://www.math.kemsu.ru/faculty/kmc/book/mko http://www.math.kemsu.ru/faculty/kmc/book/io/ http://www.allmath.ru/appliedmath.htm

Экзамен – комбинированный: экзамен – 40 баллов; семестр – 60 баллов = посещение лекций – 5, контр.раб. – 10, зачет лаб. – 3 по 15 баллов.

1

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

1.1.О связи математических методов моделирования

иисследования операций ( и в экономике, в том числе )

Под исследованием операций понимается научный подход к решению задач организационного управления [1]. В отличие от ТАУ, здесь рассматривают человеко-машинные системы. Термин “исследование операций” возник в годы второй мировой войны и означал первоначально планирование боевых операций. В современной более общей трактовке – это научная методология и технология нахождения рационально обоснованных решений в различных областях человеческой деятельности. Исследование операций охватывает вопросы построения математических моделей ситуаций, определения наилучших решений и их нахождения, анализа и практического применения.

Объектом изучения данной дисциплины являются операции, в том числе в экономике, представляющие собой совокупность действий, приводящих систему к некоторой цели. Предметом же является исследование этих операций с помощью математических методов их моделирования с целью обоснования принимаемых решений по организации оптимального управления этими операциями. Поэтому под термином «исследование операций» обычно понимают комплекс научных методов для предварительного решения задач эффективного управления организационными системами.

С ростом масштабов и сложности операций математические методы обоснования решений приобретают все большую роль. Природа систем, фигурирующих в приведенном определении под именем организационных, может быть самой различной, а их общие математические модели находят применение не только при решении производственных и экономических задач, но и в биологии, социологических исследованиях, в геологоразведке и других практических сферах. Как уже было отмечено, название дисциплины «Исследование операций» связано с применением математических методов для управления военными операциями.

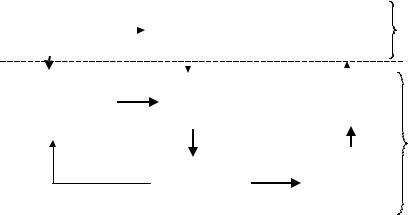
Несмотря на многообразие задач организационного управления, при их решении можно выделить некоторую общую последовательность этапов, через которые проходит любое операциональное исследование. В данном курсе изучается весь процесс исследования конкретных операций, начиная с анализа планово-экономической ситуации и кончая принципами реализации оптимального управления (рис. 1). Исключение составляет последний блок «оптимальная организация», который изучается средствами теории организаций.

2

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

I – содержательный уровень, существенно зависит от природы изучаемой системы;

II – формальный уровень, зависит от типа применяемого математического аппарата

Рисунок 1.

Таким образом, для применения количественных методов исследования требуется построить математическую модель операции. При построении модели операция, как правило, упрощается, схематизируется и схема операции описывается с помощью того или иного математического аппарата. Модель операции – это достаточно точное описание операции на подходящем математическом языке (функции, уравнения, системы уравнений и неравенств, графы и т.п.). Составление модели операции требует понимания сущности описываемого явления и знания математического аппарата одновременно. При этом отправной точкой является исходная планово-экономическая ситуация.

Однако математическое моделирование в исследовании операций является, с одной стороны, очень важным и сложным, а с другой – практически не поддающимся научной формализации процессом. Поэтому представляется целесообразным, а возможно – и единственно правильным, знакомство с техникой математического моделирования на конкретных примерах. Конечно, состав таких примеров может быть различен. В данном курсе подобраны наиболее типичные, наиболее разнообразные и наиболее часто встречающиеся на практике классические, исторически сложившиеся модели и задачи. Большинство из них использовались авторами теорий и методов для иллюстрации.

1.2. Основные понятия и определения исследования операций

Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению определенной цели. Операция есть всегда управляемое мероприятие, т.е.

3

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

имеется возможность распорядиться способом выбора некоторых параметров, характеризующих ее организацию. Эти параметры называют управляющими переменными.

Всякий определенный выбор таких переменных называется решением. Решения могут быть удачными и неудачными, разумными и неразумными. Оптимальными называют такие решения, которые по некоторым критериям предпочтительнее других.

Цель исследования операций – предварительное количественное обоснование оптимальных решений, которых может быть более одного. Окончательный выбор решения выходит за рамки исследования операций и производится средствами так называемой теории принятия решений.

Любая задача исследования операций имеет начальные «дисциплинирующие» условия, т.е. такие исходные данные, которые фиксированы с самого начала и не могут быть нарушены. В своей совокупности они формируют так называемое множество возможных решений.

Чтобы сравнивать между собой по эффективности разные решения, нужно иметь количественный критерий, называемый показателем эффективности (или целевой функцией). Этот показатель выбирается так, чтобы отражать целевую направленность операции.

Часто выполнение операции сопровождается действием случайных факторов. Тогда в качестве показателя эффективности берется не сама величина, которую хотелось бы оптимизировать, а ее среднее значение (или математическое ожидание).

Иногда операция, сопровождаемая случайными факторами, преследует такую цель А, которая может быть либо достигнута полностью, либо не достигнута совсем (типа «да – нет»). Тогда в качестве показателя эффективности выбирают вероятность достижения этой цели p(A). (Если p(A) = 0 или 1, то приходим к известной в кибернетике задаче «черного ящика».)

Неправильный выбор показателя эффективности очень опасен. Операции, организованные под углом зрения неудачно выбранного критерия, могут привести к неоправданным затратам и потерям. (Например, «вал» в качестве основного критерия оценки хозяйственной деятельности предприятия.)

1.3. Общая постановка задачи исследования операций

Задачи исследования операций делятся на две категории: а) прямые и б) обратные.

Прямые задачи отвечают на вопрос: чему будет равен показатель эффективности Z, если в заданных условиях y Y будет принято некоторое решение x X. Для решения такой задачи строится математическая модель, позволяющая выразить показатель эффективности через заданные условия и решение, а именно:

4

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

Z F(x, y),

где y заданные факторы (исходные данные),

x управляющие переменные (решение),

Z – показатель эффективности (целевая функция),

F– функциональная зависимость между переменными.

Эта зависимость в разных моделях выражается по-разному. Зависимость

между x и y обычно выражается в виде ограничений на x.

Если вид зависимости F известен, то показатель Z находится прямой подстановкой x и y в данный функционал.

Обратные задачи отвечают на вопрос: как при данных условиях y

выбрать решение x, чтобы показатель эффективности Z обратился в максимум (минимум). Такую задачу называют задачей оптимизации решения.

Пусть прямая задача решена, т.е. модель операции задана и вид зависимости F известен. Тогда обратная задача (т.е. задача оптимизации)

входящим в множество возможных решений X.

Метод поиска экстремума показателя эффективности Z и связанного с ним оптимального решения x* должен всегда выбираться, исходя из особенностей функции F и вида ограничений, накладываемых на решение. (Например, классическая задача линейного программирования.)

1.4 Иллюстративные (исторические) примеры задач исследования операций

Чтобы составить первое представление о предмете, рассмотрим не– сколько типовых задач исследования операций. Примеры взяты из книги [1].

Задача управления запасами

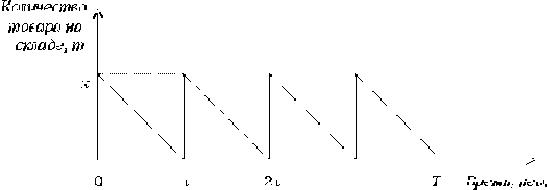
На складе хранится товар, которым обеспечивается сеть магазинов. Товар поступает на склад равными порциями через равные промежутки времени и расходуется с постоянной скоростью так, что к моменту очередного поступления его запасы становятся равными нулю (рис. 2).

5

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

Изменение запасов товара на складе во времени Рисунок 2.

Известны:

с1 - стоимость доставки одной порции товара ( руб.), с2 - стоимость хранения тонны товара в течение недели (руб./(т х нед.)),

τ - время между двумя последовательными поступлениями товара (нед.), Т - время обслуживания сети магазинов (плановый период, нед.),

N - необходимое количество товара в течение планового периода (спрос, т). Требуется определить количество товара в порции так, чтобы общие

затраты на обеспечение спроса N и хранение товара за время Т были минимальными.

Перейдем к математической формулировке задачи. Обозначим через х искомое количество товара в порции (в тоннах). Подсчитаем отдельно затраты на доставку и хранение товара. На покрытие спроса N необходимо N/x доставок товара, затраты на которые (в руб.) составят

нахождении такого положительного значения неизвестной х, при котором функция общих затрат (1.3) имеет минимум. В символической записи

6

Условие (1.4) задачи называют целевым, оно содержит требование (минимизации целевой функции), по которому находится искомое x. Условие (1.5), вытекающее из физического смысла неизвестной x, есть ограничение на x.

Задача управления запасами, содержащая ограничение на неизвестную х, относится к классу задач на условный экстремум. Конечно, здесь она предельно упрощена. Существуют более сложные постановки, которые учитывают нерегулярность поставок товара, ограниченную емкость склада и другие факторы. По образному выражению Г. Вагнера задача управления запасами "играет в исследовании операций такую же роль, как законы Ньютона в физике".

Проблема „двух картошек"

Фирма по переработке картофеля производит три вида продукции: картофельные дольки, кубики и хлопья. Анализ загруженности оборудования и спроса на рынке показывает возможность произвести и сбыть до 1.8 т долек, 1.2 т кубиков и 2.4 т хлопьев. Необходимый для переработки картофель фирма закупает у двух поставщиков. Количество готовой продукции и относительная прибыль (доход от реализации готовой продукции за вычетом стоимости сырья), которые можно получить из одной т картофеля каждого поставщика, указаны в табл. 1.1.

Таблица 1.1 Исходные данные задачи о “двух картошках”

Требуется определить, какое количество картофеля надо приобрести у каждого поставщика, чтобы обеспечить наибольшую относительную прибыль с учетом возможности сбыта готовой продукции.

Перейдем от содержательного описания ситуации к формализован–

ному. Введем неизвестные х1 и х2 - количество картофеля (т), закупаемого у поставщиков 1 и 2 соответственно. Используя три первые строки таблицы, составим балансовые соотношения

7

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

В левой части каждого неравенства записан выход готовой продукции из закупленного картофеля, а в правой части – предельные потребности в продукции на рынке сбыта. Физические размерности сравниваемых величин в балансовых соотношениях одни и те же – т. Относительная прибыль П подсчитывается с помощью последней строки таблицы и в ден. ед. равна

Условия неотрицательности (1.10) добавлены к балансовым соотношениям (1.7) - (1.9), исходя из физического смысла неизвестных.

Полученная задача называется задачей линейного программирования. Отличительная ее особенность состоит в линейности всех функций,

задающих целевое условие (1.6), ограничения (1.7) - (1.9) и условия неотрицательности (1.10).

Производственная задача «места и времени»

Компания, располагающая двумя заводами, заключила контракт на

изготовление а единиц продукции за определенный промежуток времени. Стоимость изготовления продукции в количествах х1 и х2 на заводах 1 и 2 составляет х12/ с1 и х22/ с2 ден. ед. соответственно, где с1 и с2 – известные положительные коэффициенты. Требуется распределить заказ на продукцию между заводами так, чтобы он был выполнен, и общая стоимость изготовления продукции была наименьшей.

Математическая постановка задачи достаточно очевидна. В принятых

Неравенства (1.12) отражают физический смысл неизвестных. Целевая функция (1.11) в задаче квадратичная относительно х1, х2, поэтому ее относят к задачам нелинейного (квадратичного) программирования.

Преследование Шерлока Холмса

Известный персонаж произведений английского писателя Артура Конан Дойла сыщик Шерлок Холмс оказывается однажды в довольно неприятном положении. Некто профессор Мориарти, подозреваемый Холмсом в совершении преступления, устраивает на него покушение.

8

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

Шерлок Холмс принимает решение скрыться на время в Европе. Путь из Лондона на континент лежит через портовый город Дувр. Между Лондоном и Дувром есть промежуточная железнодорожная станция Кентербери. Выбрав подходящее время и соблюдая меры предосторожности, Холмс садится на лондонском вокзале в поезд до Дувра. Когда поезд трогается, он видит через окно вагона в толпе на перроне следившего за ним Мориарти. Шерлок Холмс уверен, что Мориарти будет его преследовать, и попытается настичь следующим поездом. Перед ним возникает непростая дилемма: где лучше сойти с поезда, в Дувре или Кентербери, чтобы избежать встречи с Мориарти. Та же дилемма встает и перед профессором Мориарти, едущим за Шерлоком Холмсом на следующем поезде. Здесь мы сталкиваемся с конфликтной ситуацией, в которой интересы двух участников противоположны. Займемся ее математической формализацией. Условимся оценить жизнь Холмса в 100 условных единиц

У каждого участника конфликта есть два способа действия: сойти с поезда в Дувре или в Кентербери. Мы будем обозначать их через К и Д соответственно. В теории игр участников конфликтной ситуации называют игроками, а их возможные действия в конфликте – стратегиями. Следовательно, К и Д в данном случае – стратегии игроков.

Выбирая свои стратегии независимо, игроки создают в игре четыре возможные ситуации: КК, КД, ДК, ДД. Если считать Шерлока Холмса первым игроком, а профессора Мориарти. – вторым, то ситуация КД, например, означает, что Шерлок Холмс сходит с поезда в Кентербери и Мориарти – в Дувре. В этой ситуации Шерлок Холмс считал бы свою жизнь наполовину спасенной, т.е. получил бы в качестве выигрыша 50 условных единиц. Его выигрыши в остальных ситуациях КК, ДК, ДД составят соответственно - 100, 100, - 100 условных единиц. Отрицательный выигрыш трактуется как проигрыш.

Для наглядности удобнее представить выигрыши Шерлока Холмса табл.1.2. По существу она и есть формализованное описание конфликтной

ситуации. Хотя в таблице указаны только выигрыши первого игрока, выигрыши второго определяются автоматически. Он выигрывает ровно столько, сколько проигрывает первый игрок. Таким образом, независимо от ситуации сумма выигрышей игроков равна нулю.

Задача состоит в нахождении таких стратегий, при которых выигрыш первого игрока максимален и проигрыш второго игрока минимален.

9

Исследование операций 2012. Файл Л_1_ИсслОп.doc = Л_1_ДОп1сем.doc из "Алабин+.doc" Темы 1 и 5 и Лекция1_1.doc

По понятным соображениям приведенная игра называется

антагонистической игрой двух лиц с нулевой суммой выигрышей.

Зачет

Рассмотрим другую, более сложную, игровую ситуацию, в которой игроки имеют разные таблицы выигрышей. Речь идет о важном в студенческой и преподавательской жизни моменте – сдаче и приеме зачета. Игроками являются Студент и Преподаватель. У Студента, готовящегося к зачету, имеется две стратегии: подготовиться хорошо (Х) или плохо (П). У Преподавателя, принимающего зачет, тоже две стратегии: поставить зачет (+) или не поставить (- ). В зависимости от выбора стратегий в игре складываются четыре ситуации, которые могут приносить игрокам разное моральное удовлетворение. Оценки морального удовлетворения (в шкале с положительными и отрицательными баллами) примем за выигрыши игроков. В результате получим табл. 1.3, 1.4.

Таблица 1.3 Выигрыши Студента

По поводу оценок морального удовлетворения, указанных в таблицах, могут быть разные мнения. Например, некоторые студенты считают, что выигрыш Студента в 1 балл в ситуации, когда он выбрал стратегию П, а Преподаватель – стратегию +, явно занижен. Не вдаваясь в полемику, отметим, что проблема соответствия (адекватности) математической модели и моделируемого явления, безусловно, есть, и о ней мы будем говорить позже.

Игра, заданная таблицами 1.3, 1.4, называется биматричной. Она состоит в нахождении таких стратегий, которые обеспечивают игрокам максимальные выигрыши.

10