Программирование, вопросы / Лекц / Л_2_ИсслОп2012

Исследование операций Л_2_ИсслОп2012.doc = Л_3_ДОп1сем.doc из Лекция1_2.doc + частично "Алабин+.doc"

Лекция 2 Линейное программирование (ЛП)

О задачах ЛП. История и источники возникновения

Значительная часть практически важных задач исследования операций формируется как задачи ЛП.

К их числу относятся:

1)задача о рациональном размещении ресурсов;

2)задача об оптимальном выборе технологий;

3)задача о смесях;

4)задача о раскрое материалов;

5)транспортная задача.

( см. также Проблема „двух картошек" из Л1 )

За разработку в середине ХХ века симплексного метода решения задач ЛП ( Канторович -1939г, Данциг -1951г. симплекс-метод ) группе математиков была присвоена в 70-ые годы нобелевская премия по экономике.

Систематизация моделей ЛП

В ЛП разработано несколько методов решения задач. Эти методы, очевидно, связаны с различными типами моделей ЛП. Попытаемся выяснить, с какими.

Прежде всего следует отметить, что показатель эффективности d ЛП (целевая функция) есть линейная функция от переменных управления. Чтобы иметь экстремумы, такая функция должна быть ограничена. Действительно, любая модель ЛП помимо линейного показателя эффективности содержит ограничения на переменные управления в виде линейных равенств или неравенств. Поэтому для выяснения типов моделей ЛП достаточно задать типы показателя эффективности и типы ограничений на переменные управления.

Положим, что переменные состояния в какой-то задаче ЛП представлены двумя независимыми категориями. Им соответствуют две категории состояний системы: А1 = {аi} и А2 = {аj}. Тогда общее состояние системы есть пара (ai, aj), где аi А1, aj А2. Множество таких пар образует декартово произведение А1 ×

А2 = {(ai, aj)}, а каждой паре (ai, aj) приписывается цена с (ai, aj) = сij и количество объектов системы в этом состоянии: х(ai, aj) = хij (переменные

управления). Цена сij обычно называется стоимостью перехода от ai к aj. Рассмотрим пару множеств А1 и А2. Принято различать следующие случаи

их задания.

1-й случай: А1 А, А2 = . Пример: А есть множество типов изделий, А1 – множество выпускаемых типов изделий на данном предприятии. Тогда сi – цена одного изделия, а хi – количество изделий i-го типа. Целевая функция при этом выражается в векторной форме:

1

Исследование операций Л_2_ИсслОп2012.doc = Л_3_ДОп1сем.doc из Лекция1_2.doc + частично "Алабин+.doc"

Fц сi xi.

i

2-й случай: А1 А, А2 В. Множества А и В принципиально различны. Пример: А есть типы изделий, В – типы технологий. Тогда сij – стоимость одного изделия, а хij – количество изделий i-го типа из А1, изготовленных по j-й технологии из А2. Целевая функция выражается в матричной форме:

Fц cij xij i j

с разнородными наборами А1 и А2.

3-й случай: А1 А, А2 А. Пример: множество А – различные пункты, А1 – пункты отправления, А2 – пункты назначения. Тогда сij – цена доставки, а хij – количество единиц продукции, доставляемых из ai в aj; ai А1, aj А2. Целевая функция выражается в матричной форме:

Fц cij xij i j

с однородными наборами А1 и А2.

Что касается ограничений на переменные управления хi и xij, то здесь достаточно различать лишь два случая: 1) хi, xij 0 и 2) хi, xij = 0,1 (т.е. непрерывные или дискретные переменные), так как здесь возникают принципиально различные алгоритмы.

Полученные результаты полезно представить в следующем виде (табл. 1).

Таблица 1

Для каждого из шести типов моделей ЛП возникает свой тип задач, которые, как правило, имеют теоретически разработанные методы решения:

1.Задачи самого общего вида. Специально для таких задач разработан универсальный метод решения – симплекс-метод.

2.Частный случай (1), но эффективных алгоритмов в ЛП нет. В принципе можно свести к симплекс-методу.

3.Задачи распределения или назначения общего вида. Сводятся к типу (1), но некоторые задачи имеют специфические алгоритмы.

2

Исследование операций Л_2_ИсслОп2012.doc = Л_3_ДОп1сем.doc из Лекция1_2.doc + частично "Алабин+.doc"

4.Частный случай типа (3), эффективных алгоритмов в ЛП нет. 5.Т-задачи. Наиболее разработанный тип задач под названием

«Транспортные задачи». Имеют хорошо разработанную математическую теорию решения (распределительный метод, метод потенциалов, обобщенный венгерский метод).

6.Частный случай типа (5): задачи «О назначениях». Весьма эффективно решаются венгерским методом, но могут быть решены любым алгоритмом Т- задачи.

Замечания

Все методы ЛП, кроме симплекс-метода, привязаны к специфике решаемых классов задач и поэтому неотделимы от их конкретных математических моделей.

Решение конкретной прикладной задачи осуществляется сведением (если это возможно) ее модели к типовой модели какого-либо метода.

Возможные исходы решения задач ЛП

Выше было указано, что всякая модель ЛП содержит ограничения на линейную функцию Fц, которая в противном случае не может иметь экстремумов. Однако ограничения, задавая область допустимых решений, могут быть сами заданы некорректно. Может при этом оказаться, что допустимых решений нет вовсе. Например, если плановые задания на выпуск каких-то изделий завышены, то ресурсов задачи может оказаться недостаточно для их реализации. Ниже (табл. 2) приводятся все возможные случаи.

В общем случае множество допустимых решений в координатах переменных управления из-за линейности ограничений образует выпуклый многогранник, называемый симплексом ( не совсем корректно: см. алгебраическую топологию ). Конечно, симплекс может вырождаться в более простую конфигурацию, даже в точку, или быть пустым. Прокомментируем отдельные случаи:

1)задача имеет единственное решение;

2)если решений хотя бы два, то все точки на линии, их соединяющей, также являютсярешениями;имеемальтернативныйоптимум;

3

Исследование операций Л_2_ИсслОп2012.doc = Л_3_ДОп1сем.doc из Лекция1_2.doc + частично "Алабин+.doc"

3)отсутствие решения еще не говорит об отсутствии экстремума вообще: экстремум есть, но не тот, который требуется в задаче;

4)в этом случае max{ min Fц } = min{ max Fц }. Это самый благоприятный исход в экономических задачах, иногда его можно получить анализом исходных данных, преобразуя количество ресурсов без дополнительных затрат; при этом opt Fц только улучшается за счет полного использования ресурсов;

5)если допустимых решений нет, то и оптимальных быть не может.

Сматематической точки зрения четвертый и пятый случаи являются вырожденными.

Задачи ЛП в векторной форме

В этом разделе будут изучены экстремальные свойства линейных функций n переменных, которые записаны в одном из следующих эквивалентных видов:

F x1,x2,...,xn F x c1x1 c2x2 ... cnxn n cixi

i 1

и универсальный аналитико-численный метод решения задачи ЛП – симплекс-

метод Данцига (СМ).

Общая задача ЛП (ОЗЛП)

где F x - целевая функция – линейная функция n переменных.

Ограничения на x задаются линейными равенствами и(или) неравенствами с коэффициентами aij и правой частью bi. Все cj ,aji ,bi вещественные числа.

Требуется найти x* - вектор, доставляющий целевой функции F x экстремальные значения.

В ЛП x* называется оптимальным планом.

Симметричная задача ЛП

Существуютдва вида симметричной задачи:

4

Исследование операций Л_2_ИсслОп2012.doc = Л_3_ДОп1сем.doc из Лекция1_2.doc + частично "Алабин+.doc"

Переход от симметричной формы записи ЛП к канонической

Осуществляем путем введения неотрицательных дополнительных

(балансовых) переменных: xn i 0, i 1,m.

В симметрической задаче 1-го вида (задачи на max) в систему неравенств, определяющих , дополнительная переменная вводится следующим образом:

Аналогично для симметричной задачи 2-го вида (на min) вводятся дополнительные балансные переменные:

j 1

: xj 0xn i 0

Вцелевую функцию F x дополнительные (балансовые) переменные

входят с коэффициентом равным нулю (т.е. не учитываются).

Учитывая важность канонической формы записи задачи ЛП, представим ее, используя матрицы и векторы:

5

Исследование операций Л_2_ИсслОп2012.doc = Л_3_ДОп1сем.doc из Лекция1_2.doc + частично "Алабин+.doc"

F x cT x min(max)

x Rn

: Ax A0 , где матрицы коэффициентов и неизвестных:

x 0

Переход от канонической формы записи задачи ЛП к симметричной. Представление целевой функции как функции только от свободных

переменных

Предположим, что в системе линейных уравнений (9) имеется m линейнонезависимых уравнений, т.е. ранг системы равен m. Поскольку m n, то, как известно, такая система будет иметь бесконечное множество решений; именно при таком условии (m n), оптимизационная задача имеет смысл. Если бы m n, то система имела бы одно единственное решение при условии 0, - определитель системы. Тогда нет возможности выбора оптимальной системы.

Для того, чтобы преобразовать (9) в систему линейных неравенств симметричной задачи ЛП (3), необходимо, используя, например, метод Гаусса решения системы линейных уравнений, выделить базисные переменные:

Коэффициенты ij и i определенным образом зависит от aji и bi .

Для того, чтобы завершить переход от канонической записи к записи задач ЛП к ее симметричной записи, необходимо представить целевую функцию

свободными (независимыми), а переменные x1,x2,...,xm называются базисными

(зависимыми).

Выразим целевую функцию только через свободные переменные.

6

Исследование операций Л_2_ИсслОп2012.doc = Л_3_ДОп1сем.doc из Лекция1_2.doc + частично "Алабин+.doc"

Заметим, что это выражение для целевой функции эффективно используется в симплекс-методе решения задач ЛП.

Геометрическая интерпретация задачи ЛП и графо-аналитический метод ее решения

Пусть в задаче ЛП после подстановки базисных, осталось только две свободных переменные. Тогда в R2 она имеет вид:

F x1,x2 c1x1 c2x2 min(max)

11x1 12x2 121x1 22x2 2

: .........................

m1x1 m2x2 mx1,x2 0

ОДР - выпуклое множество, т.к. каждое из неравенств определяет полуплоскость (выпуклое множество); их пересечение дает замкнутую область, которая будет выпуклым множеством.

Напомним, что множество в Rn называется выпуклым, если выполняется условие:

7

Исследование операций Л_2_ИсслОп2012.doc = Л_3_ДОп1сем.doc из Лекция1_2.doc + частично "Алабин+.doc"

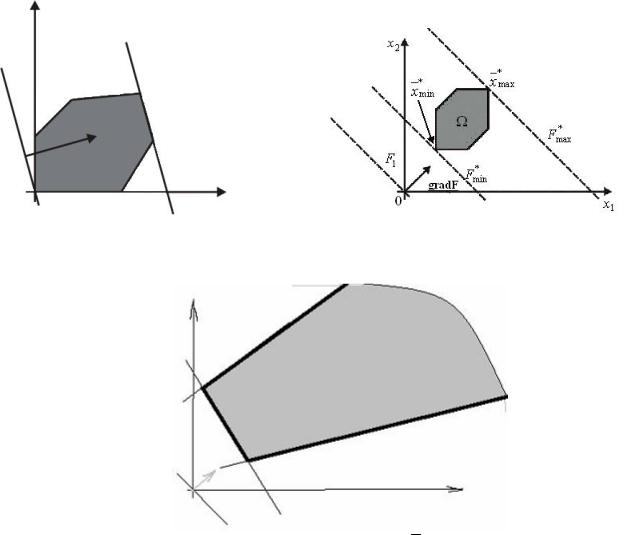
направлении grad F x1,x2 до граничных точек многоугольника . Изобразим графически наиболее характерные случаи решения задачи ЛП в

пространстве R2. x2

Множество и целевая функция F x неограниченны.

8