Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский национальный университет радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Л_10_ИсслОп

.pdf

Скачиваний:

Добавлен:

14.04.2015

Размер:

694.53 Кб

Скачать

☆

Файл Л_10_ИсслОп = "ДинПрогр Лекц1.doc" из "I:\RES_H\WORK\EDUCATION\ХНУРЭ - учебные курсы\ИССЛЕД_ОПЕР\МОЁ\Лекц 2 семестр\Динамическое программ\из IASA - зайченко\"

Лекция 10

Для решения задач оптимизации многостадийных процессов, а также для процессов, которые могут быть математически описаны как многостадийные (Рис.1), применяется метод динамического

программирования.

Рисунок 1. Многостадийный процесс.

Замечание. Под «стадией» процесса следует понимать не только момент времени.

Динамическое программирование - это вычислительный метод для решения задач оптимизации специальной структуры с аддитивными или мультипликативными целевыми функциями.

Динамическое программирование возникло и сформировалось в 1950-1953 гг. благодаря работам Р. Беллмана и его сотрудников. Первые задачи, которые привели к появлению вычислительного метода, были динамическими задачами управления запасами.

Динамическое программирование применяется для оптимизации

математически описанных процессов. Поэтому в дальнейшем для многостадийного процесса предполагается известным математическое описание каждой его стадии, которое представляется в общем виде системой уравнений:

xk(i) 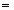jk(i)(x1(i-1), …, xm(i-1), u1(i), …, ur(i)),

k 1, ..., m; i 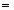1, ..., N,

связывающей выходные внутренние параметры i-й стадии xk(i) с выходными внутренними параметрами предыдущей стадии xk(i-1) и внешними параметрами – управлением иl(i) (l 1, ..., r), используемым на i-й стадии.

Систему уравнений удобно также представить в векторной форме

x(i) j(i)(x(i-1), u(i)),

где x(i) – вектор переменных состояния (или выход) i-й стадии:

x(i) (x1(i), x2(i), …, xm(i)),

a u(i) - вектор управляющих воздействий (управление) на i-й стадии:

u(i) (u1(i), u2(i), …, ur(i)).

Состояние m мерного объекта – точку в фазовом пространстве – определяет на i-й стадии весь вектор x(i). Размерности векторов состояния x(i) и управления и u(i) в общем случае могут быть различными для разных стадий процесса. Однако далее, не нарушая общности, можно принять, что размерности m и r векторов состояния и управления для всех стадий процесса одинаковы.

В реальных процессах на значения переменных состояния x(i) и управляющих воздействий u(i) могут быть наложены ограничения, определяющие диапазон изменения или взаимосвязь указанных переменных. Математически это находит выражение в появлении дополнительных условий в виде равенств или неравенств с функциями

Fj(x(1), …, x(N), u(1), …, u(N)) в левой части,

которые должны учитываться при решении задачи оптимизации.

В дальнейшем при необходимости отметить, что значения переменных состояния или управляющих воздействий удовлетворяют ограничениям, будем использоваться запись:

Смысл записи заключается в том, что значения переменных x(i) и u(i) принадлежат к допустимым областям их изменения Х и U, ограниченным соответствующими соотношениями.

Предполагается, что эффективность каждой стадии процесса оценивается некоторой скалярной величиной

ri 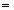ri*(x(i), u(i)).

заданной в виде функции от переменных состояния i-й (текущей) стадии x(i) и принятого на ней управления u(i).

С учетом математического описания стадии функциональная зависимость эффективности может быть представлена также как

ri ri(x(i-1), u(i)).

т. е. как функция входа x(i-1) на i-й стадии (т.е., состояния на предыдущей стадии) и используемого на ней управления u(i)

Результирующая оценка эффективности многостадийного процесса в целом определяется как аддитивная функция результатов, получаемых на каждой стадии:

Естественно, что значение критерия оптимальности RN зависит от совокупности uN –управляющих воздействий на всех стадиях процесса, которые представляет собой набор значений векторов u(i) для всех стадий:

uN 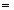(u(1), u(2), …, u(N)).

Эту совокупность управлений для всех стадий процесса uN будем называть в дальнейшем стратегией управления многостадийным. процессом или просто стратегией управления.

Таким образом, задачу оптимизации многостадийного процесса можно сформулировать как задачу отыскания оптимальной стратегии

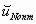
(uопт(1), uопт(2), …, uопт(N)),

для которой критерий оптимальности Rn принимает, в зависимости от постановки оптимальной задачи, максимальное или минимальное значение.

Принцип оптимальности

Воснову метода динамического программирования положен принцип оптимальности, который в переложении для много-, стадийного процесса

может быть сформулирован следующим образом. Оптимальная стратегия обладает тем свойством, что каковы бы ни были начальное состояние x(0) многостадийного процесса и управление на первой стадии u(1), последующие управления на всех стадиях u(i) (i 2, ..., N) должны составлять оптимальную стратегию иN-1 относительно состояния x(1) первой стадии, определяемого начальным состоянием процесса x(0) и управлением на первой стадии u(1).

Вприведенной формулировке принципа оптимальности под оптимальной

стратегией иN-1 понимается стратегия управления многостадийным процессом, включающим N-1 последних стадий исходного процесса, придающая критерию

оптимальное значение. (внизу – i=2 !!)

Другими словами, оптимальная стратегия иN-1 находится для (N-1)- стадийного процесса, для которого величина является начальным состоянием.

Таким образом, если известна оптимальная стратегия управления иN-1 для любого возможного состояния x(1) первой стадии N-стадийного процесса, то уже не составляет труда выбрать оптимальное управление и на первой стадии uопт(1), поскольку на последующих стадиях оно определяется только состоянием выхода первой стадии:

иN-1 иN-1 (x(1)).

Процедура применения принципа оптимальности для оптимизации N- стадийного процесса, очевидно, должна начинаться с последней стадии процесса, для которой не существует последующих стадий, могущих повлиять согласно принципу оптимальности на выбор управления uопт(N) на этой стадии. После того как оптимальное управление uопт(N) найдено для всех возможных состояний входа последней стадии x(N-1) 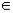X, можно приступить к определению оптимального управления для предыдущей (N-1)-стадии, для которой оптимальная стратегия управления на последующих стадиях (т. е. на последней N-й стадии) известна, и т. д.

В результате может быть найдена оптимальная стратегия управления для всего многостадийного процесса, являющаяся функцией начального состояния процесса uN(x(0)). Если начальное состояние x(0) известно (задано или выбрано из условия оптимума критерия R), то его значение определяет оптимальные управления для всех стадий процесса.

Идею вычислительного метода динамического программирования (ДП) для «не временной» модели рассмотрим на следующем примере:

Максимизировать	(1)






при условиях		(2 )

Как видно, целевая функция задачи и ограничение являются суммой функций от одной переменной каждая. Такая функция, как известно, называется

аддитивной. Если все 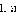выпуклые, то для решения задачи можно применить метод множителей Лагранжа.

Если имеется много локальных минимумов, то этот метод дает лишь один из них. Если надо найти глобальный максимум, метод множителей Лагранжа применить невозможно.

Поэтому рассмотрим другой метод, обеспечивающий отыскание глобально-

оптимального решения. Предположим, что все - целые числа. Предположим также, что в рассматриваемой задаче все переменные могут принимать лишь целочисленные значения.

Через обозначим абсолютный (глобальный) максимум при условии

. Выберем некоторое значение

и, зафиксировав его,

максимизируем	по всем остальным переменным	.

Предположим, что такая максимизация проведена для всех возможных

значений . Тогда будет наибольшим из всех возможных значений . Формально этот процесс (эта процедура) записывается так:

(3)

причем

(4)

Все aj без ограничения общности можно считать единицами. ( замена: xj:= aj xj ).

Поскольку

для неотрицательных целых чисел,

удовлетворяющих условию (4), зависит от , то обозначим

(5)

Предположим, что мы вычислили для всех допустимых целых

значений

, где

означает целую часть .

Очевидно, что

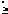
. (6)

Для вычисления (6) определим и для всех допустимых значений и выберем максимальное . Одновременно найдем оптимальное решение . Таким образом, если бы была известна функция

, то вся задача свелась бы к задаче с одной переменной.

Покажем, как вычислить .

Обозначим

см. (5)

при условии

. см. (4)

Повторив вышеприведенные выкладки, получим

(7)

где

(8)

причем максимум в (7) отыскивается при условии

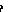
Аналогичным образом вычисляем и т.д. В конце концов на - м шаге мы используем 'основное рекуррентное соотношение (ОРС) динамического программирования'

(9)

при условии, что

Используя ОРС (9), организуем процесс вычислений, как многошаговый процесс, следующим образом. На первом шаге, зафиксировав начало интервала 0 и изменяя его правый конец , вычисляем

(10)

для всех возможных значений =0, 1, . , b. Оптимальное решение первого

шага обозначим через . Составляем таблицу динамического программирования первого шага (табл.1), и заполняем ее результатами вычислений.

На второмшаге ( =2)находим всоответствииссоотношением

, (11)

причем значения берем из табл. 1.

Вычисляем последовательно для всех значений = 0,1,.,, используя

результаты табл.1. Одновременно находим и . Результаты вычислений заносим в таблицу второго шага (табл. 2).

Таблица 1	Таблица 2
0	0
1	1

Дале, пользуясь соотношением (8), последовательно вычисляем

для всех значений

= 0, 1, 2, ., .

В конце концов, на последнем шаге при находим

, (12)

а также соответствующее оптимальное значение для последней переменной

. Для отыскания значений всех остальных переменных

надо воспользоваться таблицей											и т.д. шагов.

Полагая , из таблицы предшествующего шага находим (без вычислений)

Следовательно, динамическое программирование - это направленный последовательный перебор вариантов, который обязательно приводит к глобальному максимуму. Для применения метода необходимо табулировать

функции , . , для всех допустимых значений .