
2-Konspekt_lektsiy_MS
.pdf5.3.1 Загальна характеристика методу статистичного моделювання На етапі дослідження і проектування систем при побудові та реалізації
машинних моделей (аналітичних та імітаційних) широко використовується метод статистичних випробувань (Монте-Карло), що базується на використанні випадкових чисел, тобто можливих значень деякої випадкової величини із заданим розподілом імовірностей. Статистичне моделювання є методом одержання за допомогою ЕОМ статистичних даних щодо процесів, які відбуваються в досліджуваній системі S . Для одержання оцінок характеристик об’єкта статистичні дані обробляються і класифікуються з використанням методів математичної статистики.
Сутність методу статистичного моделювання зводиться до побудови для процесу функціонування досліджуваної системи S деякого моделювального алгоритму, що імітує поводження і взаємодію елементів системи з урахуванням випадкових вхідних впливів і впливів зовнішнього середовища Е, і реалізації цього алгоритму з використанням програмно-технічних засобів ЕОМ.
Розрізнюють дві області застосування методу статистичного моделювання: для дослідження стохастичних об’єктів та для розв’язання детермінованих задач. Основною ідеєю, що використовується під час розв’язання детермінованих задач методом статистичного моделювання, є заміна детермінованої задачі еквівалентною схемою деякої стохастичної системи, вихідні характеристики якої збігаються з результатом розв’язання детермінованої задачі. Природно, що при такій заміні замість точного розв’язку задачі знаходиться наближений, похибка якого зменшується зі збільшенням кількості випробувань (реалізацій моделювального алгоритму) N.
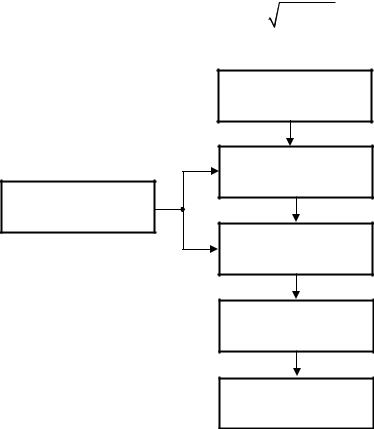
Як результат статистичного моделювання системи S отримують серію часткових значень шуканих величин або функцій, статистична обробка яких дозволяє одержати відомості щодо поводження реального об’єкта або процесу в довільні моменти часу (рис. 5.2). Якщо кількість реалізацій алгоритму N є досить великою, то отримані результати моделювання системи здобувають статистичну стійкість і з достатньою точністю можуть бути прийняті як оцінки шуканих характеристик процесу функціонування системи S .
Теоретичною основою методу статистичного моделювання систем на ЕОМ є граничні теореми теорії ймовірностей (Чебишева, Бернуллі, Пуассона, центральна гранична), які гарантують високу якість статистичних оцінок при досить великій кількості випробувань (реалізацій) N. Практично прийнятні при статистичному моделюванні кількісні оцінки характеристик систем часто
60
можуть бути отримані вже при порівняно невеликих значеннях N.
Використання статистичного моделювання для дослідження стоха-
стичних систем. Необхідно методом статистичного моделювання знайти оцінку вихідної характеристики стохастичної системи SR , функціонування якої
описується такими співвідношеннями: x =1−e−λ – вхідний вплив; v =1−e−ϕ – вплив зовнішнього середовища (де λ та ϕ – випадкові величини, для яких відомі їхні функції розподілу). Метою моделювання є оцінка математичного сподівання М[y] величини y, залежність якої від вхідного впливу х і впливу
зовнішнього середовища v має вигляд y = x2 + v2 .
Генерація випадкових чисел
Імітація випадкових впливів
Вхідні дані
Обчислення співвідношень моделі
Реєстрація
результатів
Статистична обробка результатів
Рисунок 5.2 – Схема методу статистичного моделювання
Як |
оцінку математичного |
сподівання |
М[y] використаємо середнє |
||||
|
|
N |
(де yi – випадкове значення величини y; |
|
|||
арифметичне: y = (1/ N )∑ yi |
N – |
||||||
|
|
i=1 |
|
|
|
|
|
кількість |
реалізацій, необхідна для статистичної стійкості результатів). |
|
|||||
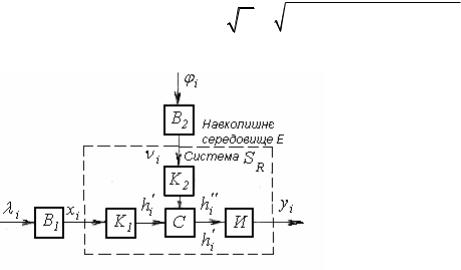
Елементи структурної |
схеми |
системи |
SR |
(рис, 5.3) виконують |
такі |
||
функції: |
|
|
|
|
|
|
|
– |
обчислення B : x =1−e−λi |
; v =1−e−ϕi ; |
|
|
|||
|
1 |
i |
|
i |
|
|
|
– |
піднесення до квадрата: K1 : hi′ = (1−e−λi )2 ; |
hi′′= (1−e−ϕi )2 ; |
|
||||
|
|
|
|
61 |
|
|
|
– |
підсумовування С: hi = hi′ + hi′′= (1−e−λi )2 + (1−e−ϕi )2 ; |
|
|
|
– |
добування кореня квадратного И: y = |
h = (1−e−λi |
)2 |
+ (1−e−ϕi )2 . |
|
i |
i |
|
|
Рисунок 5.3 – Структурна схема стохастичної системи SR
Ця модель дозволяє одержати методом статистичного моделювання оцінку математичного сподівання вихідної характеристики М[y] стохастичної системи SR , точність і вірогідність якої визначатиметься виконаною кількістю реалізацій N.
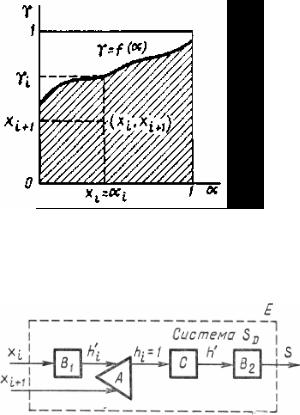
Використання статистичного моделювання для розв’язання детермінованих задач. Необхідно методом статистичного моделювання знайти оцінку площі фігури (рис. 5.4), обмеженої осями координат, ординатою α =1 і кривою γ = f (α) . Вважатимемо, що 0 ≤ f (α) ≤1 на всьому відрізку 0 ≤α ≤1.
Ця задача є детермінованою, а її аналітичне розв’язання зводиться до
1
обчислення визначеного інтеграла , тобто шукана площа фігури S = ∫ f (α) dα .
0
Для розв’язання цієї детермінованої задачі методом статистичного моделювання необхідно попередньо побудувати адекватну за вихідними характеристиками стохастичну систему SD (рис. 5.5), оцінки характеристик якої збігатимуться із шуканими в даній детермінованій задачі.
Елементи структурної схеми системи SD виконують такі функції:
– обчислення B1 : hi′ = f (xi ) ;
– аналіз А: hi =1, if xi+1 ≤ f (xi ); else 0 if f (xi ) > xi+1 ;
– підсумовування С: hi′ = ∑hi ;
62
– обчислення B2 : S = h′/ N (де N – кількість реалізацій, що необхідна для статистичної стійкості результатів).
Рисунок 5.4 – Геометрична інтерпретація оцінки площі фігури
Рисунок 5.5 – Структурна схема еквівалентної стохастичної системи SD
Система SD функціонує в такий спосіб: вибирається пара незалежних випадкових чисел із рівномірним розподілом на інтервалі [0, 1], що визначають координати точки (xi , xi+1) (рис. 5.4), обчислюється ордината γi = f (xi ) і проводиться порівняння величин γi та xi+1. Якщо точка (xi , xi+1) потрапила в площу фігури (у тому числі й на криву f (α) ), то результат випробування вважається позитивним hi =1. У підсумку можна визначити статистичну площу фігури для заданої кількості реалізацій N.
5.3.2 Способи генерації випадкових чисел При статистичному імітаційному моделюванні систем на ЕОМ важливе
значення має врахування всіх суттєвих випадкових факторів і впливів. Для їх формалізації використовують випадкові події, дискретні та неперервні величини, вектори і процеси. Формування на ЕОМ реалізацій випадкових об’єктів будь-якої природи зводиться до генерації та перетворення
63
послідовностей випадкових чисел. При дискретному моделюванні базовим
процесом є |
послідовність чисел { xi } = x0 , x1 ,..., xN , |
що є реалізацією |
незалежних, |
рівномірно розподілених на інтервалі (0, 1) |
випадкових величин |
{ ξi } = ξ0 , ξ1 ,..., ξN .
Слід враховувати, що для методу статистичного моделювання на ЕОМ характерними є велика кількість операцій (машинного часу), що витрачаються на дії з випадковими числами, та суттєва залежність отримуваних результатів від якості вихідних (базових) послідовностей випадкових чисел. Це робить актуальним створення простих і економічних способів формування послідовностей випадкових чисел.
До ідеального генератора ставиться ряд вимог. Зокрема, послідовності, що видаються ним, мають:
–складатися із рівномірно розподілених чисел;
–містити статистично незалежні числа;
–бути відтворюваними;
–містити числа, що не повторюються;
–створюватися із мінімальними витратами машинного часу;
–займати мінімальний обсяг машинної пам’яті.
Найпоширенішими на практиці є три основних способи генерації випадкових чисел: апаратний (фізичний), табличний (файловий) і алгоритмічний (програмний).
Апаратний спосіб. При цьому способі генерації випадкові числа виробляються спеціальною електронною приставкою – датчиком випадкових чисел. Реалізація цього способу не потребує додаткових обчислювальних операцій ЕОМ з генерації випадкових чисел (необхідна операція звертання до зовнішнього датчика). Як фізичний ефект, що лежить в основі таких генераторів, найчастіше використовуються шуми в електронних і напівпровідникових приладах та явища розпаду радіоактивних елементів.
Перевагами цього способу генерації є: необмежений запас чисел; мінімум машинних операцій та пам’яті. Його недоліками є: необхідність періодичної перевірки якості послідовності; неможливість відтворення послідовності; необхідність використання спеціального пристрою.
Табличний спосіб. При цьому способі випадкові числа, оформлені у вигляді таблиці, поміщають в пам’ять ЕОМ, попередньо сформувавши з них відповідний файл.
Перевагами цього способу генерації є: одноразова перевірка якості
64
послідовності; можливість відтворення послідовностей. Його недоліками є: великі витрати оперативної пам’яті (або часу при розміщенні файла в зовнішній пам’яті).
Алгоритмічний спосіб. При використанні цього способу випадкові числа формуються ЕОМ за допомогою спеціальних алгоритмів і реалізуючих їх програм.
Перевагами цього способу генерації є: можливість відтворення послідовностей; використання відносно невеликого обсягу пам’яті. Його недоліками є: обмеженість розміру послідовності її періодом; суттєві витрати машинного часу.
Як найбільш раціональний на практиці при моделюванні систем управління на універсальних ЕОМ найчастіше використовується алгоритмічний спосіб одержання випадкових чисел. При цьому, з урахуванням детермінованого характеру алгоритмів, отримувані з їх допомогою числа вважаються псевдовипадковими з квазірівномірним розподілом.
5.3.3 Процедури генерації випадкових чисел Найпоширеніше застосування в практиці моделювання на ЕОМ для
генерації послідовностей псевдовипадкових чисел знаходять алгоритми виду
Х1+1 = Ф(хі), |
(5.1) |
що є рекурентним співвідношенням першого порядку, для яких початкове число х0 і параметри оператора Ф(х) мають бути задані.
Історично однією з перших процедур одержання псевдовипадкових чисел була процедура методу серединних квадратів. Нехай є 2п-розрядне число,
менше за 1: x0 = 0,a1a2 ... a2n . Піднесемо його до квадрата: x02 = 0,b1b2 ...b4n , а потім відберемо середні 2п розрядів, які й будуть дробовою частиною
наступного числа псевдовипадкової послідовності x1 = 0,bn+1bn+2 ...b3n .
Наприклад, якщо початкове число х0 = 0,3771, то x02 = 0,14220441, а х1 = 0,2204,
потім x12 = 0,04857616 , а х2=0,8576 і т.д.
Недоліками цього методу є наявність кореляції між числами послідовності, а також можливість виродження послідовності, тобто х=0, починаючи з деякого значення i ≥ i * . Це істотно обмежує можливості використання методу серединних квадратів.
65
Широке застосування при моделюванні систем на ЕОМ одержали конгруентні процедури генерації псевдовипадкових послідовностей, що реалізуються послідовностями арифметичних операцій, в основі яких лежить фундаментальне поняття конгруентності.
Два цілих числа α і β конгруентні (порівняні) за модулем m , де m – ціле число, тоді й тільки тоді, коли існує таке ціле число k , що α − β = km , тобто якщо різниця α − β ділиться на m і числа α і β дають однакові залишки від ділення на абсолютну величину числа m . Наприклад, 5617 = 12 (mod 5), 5008=8 (mod 1000).
Конгруентні процедури є чисто детермінованими й описуються у вигляді рекурентного співвідношення, коли функція. (5.1) має вигляд
Xi +1 = λ Xi + μ(mod M ), |
(5.2) |
де X i , λ, μ, M – невід’ємні цілі числа. Розкриємо рекурентне співвідношення (4.10):
Якщо задано початкове значення Х0, множник λ і адитивна константа μ, то (5.2) однозначно визначає послідовність цілих чисел {Хі}, складену із залишків від ділення на М членів послідовності {{ λi x0 + μ( λi −1) /( λ −1 )} . Таким чином, для будь-якого i ≥1 справедлива нерівність Xi < M . За цілими числами послідовності {Хі} можна побудувати послідовність {хі} = {Хі /М} раціональних чисел з одиничного інтервалу (0, 1).
Конгруентна процедура може бути реалізована мультиплікативним методом (частковий випадок співвідношення (5.2) для μ = 0 ), що подається у вигляді: X i +1 = λ X i (mod M ). Він є простішим за змішаний метод (5.2) на одну операцію додавання.
Через детермінованість конгруентного методу можливим є відтворення послідовностей. Необхідний обсяг машинної пам’яті при цьому мінімальний, а точки зору обчислень необхідним є послідовний підрахунок добутку двох цілих чисел, що швидко реалізується сучасними ЕОМ.
5.3.4 Імітація випадкових подій Нехай маємо випадкові числа хі, тобто можливі значення випадкової
величини ξ , рівномірно розподіленої в інтервалі (0, 1). Необхідно реалізувати випадкову подію А, що настає із заданою ймовірністю р. Визначимо А як подію,
66
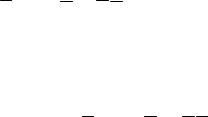
що відповідає виконанню умови xi ≤p . Тоді ймовірність події А буде
p
P( a ) = dx = p . Протилежна подія |
A |
полягає в тому, що x > p , а ймовірність |
|||
∫ |
i |
||||
0 |
|
|
|
|
|
протилежної події P( |
|
) =1 − p . |
|
||
A |
|
||||
Процедура моделювання в цьому випадку полягає у генерації хі і |
|||||
порівнянні їх зі значенням р. При цьому, якщо умова |
xi ≤p виконується, то |
||||
результатом випробування є подія А. |
|
||||
У такий же спосіб можна імітувати настання групи подій. Нехай А1, А2,
..., Ar – |
повна група подій, |
що |
настають із |
ймовірностями |
p1 , p2 ,..., pr |
||
відповідно. Визначимо Am як |
подію, яка полягає в тому, що |
значення |
хі |
||||
випадкової величини ξ |
задовольняє нерівності |
|
|
|
|||
|
|
|
lm−1 < xi ≤ lm , |
|
(5.3) |
||
|
m |
|
|
|
|
|
|
де lm = ∑pi . |
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
P( Am ) = |
lm |
|
|
|
|
|
Тоді |
∫dx = pm |
, а |
процедура |
моделювання |
полягає |
у |
|
|
lm-1 |
|
|
|
|
|
|
послідовному порівнянні випадкових чисел xi зі значеннями lm . Результатом випробування є подія Am , якщо виконується умова (5.3). Цю процедуру називають визначенням результату випробування за жеребом відповідно до ймовірностей p1 , p2 ,..., pr .
Процедуру імітації складних подій можна розглядати як розвиток попередніх. Нехай незалежні події А та В мають імовірності настання pA та pB відповідно. Можливими результатами спільних випробувань у цьому випадку будуть події AB , AB , AB , AB , що настають із імовірностями pA pB ,
( 1 − pA )pB , pA( 1 − pB ), ( 1 − pA )( 1 − pB ).
Для моделювання спільних випробувань можна використати два варіанти процедури: послідовну перевірку умов xi ≤pA і xi +1 ≤pB або визначення
одного з результатів AB , AB , AB , AB за жеребом з відповідними ймовірностями за умовою (5.3).
Перший варіант процедури може бути використаний для імітації у випадку, коли події А та В є залежними і настають із імовірностями pA та pB .
67

Позначимо через Р(В/А) умовну ймовірність настання події В за умови, що подія А відбулася. При цьому вважаємо, що умовна ймовірність Р(В/А) задана. Із послідовності випадкових чисел { xi } вибирається число xm . Якщо умова xm ≤pA виконується, то має місце подія А. Для випробування, пов’язаного з подією В, використовується ймовірність Р(В/А). Із послідовності випадкових чисел { xi } вибирається число xm+1 і перевіряється виконання умови xm+1 ≤Р(В/А). Залежно від того, виконується чи ні ця нерівність, результатом
випробування є AB або AB .
Якщо нерівність xm ≤pA не виконується, то має місце подія A . Для випробування, пов’язаного з подією В, необхідно визначити ймовірність P( B / A ), вибрати із послідовності { xi } число xm+1 і перевірити виконання умови xm+1 ≤Р( B / A ). Залежно від її виконання результатом випробування будуть AB , AB .
5.3.5Генерація випадкових величин із заданим законом розподілу
Упроцесі моделювання може поставати необхідність генерації випадкових величин не тільки з рівномірним, але й з іншими (заданими умовами задач) законами розподілу.
Безперервна випадкова величина η задана інтегральною функцією
розподілу:
y
Fη( y ) = P( η≤y ) = ∫fη( y ) dy ,
∞
де fη( y ) – щільність імовірностей.
Для одержання безперервних випадкових величин із заданим законом розподілу (як і для дискретних величин) використовують точний метод зворотної функції та наближені методи.
Метод зворотної функції засновано на тому, що взаємно однозначна монотонна функція η = F -1(ξ ), отримана шляхом розв’язання відносно η рівняння ξ = Fη( y ) , перетворює рівномірно розподілену на інтервалі (0, 1) величину ξ в η із необхідною щільністю fη( y ) . Виходячи з цього, щоб одержати число, яке належить послідовності випадкових чисел { yi }, що мають
68
функцію щільності / fη( y ) , необхідно розв’язати відносно yi |
рівняння |
yi |
|
∫fη( y ) dy = xi . |
(5.4) |
∞
Нехай необхідно одержати випадкові числа з показниковим законом
розподілу fη( y ) = λe λy , y > 0 . |
|
|
|
yi |
λy dy = x |
, |
де x – |
Відповідно до співвідношення (5.4) одержимо λ e |
|||
∫ |
|
i |
i |
o |
|
|
|
випадкове число, що має рівномірний розподіл в інтервалі (0,1). Розв’язавши
рівняння, |
отримаємо yi = −( 1 / λ ) ln ( 1 − xi ). З огляду |
на те, що випадкова |
величина |
ξ1 = 1 ξ має також рівномірний розподіл в |
інтервалі (0,1), можна |
записати yi = - ( 1 / λ ) ln xi .
Цей спосіб одержання випадкових чисел із заданим законом розподілу має обмежену сферу застосування в практиці моделювання систем на ЕОМ, що пояснюється такими обставинами: для багатьох законів розподілу інтеграл (5.4) не береться і доводиться використовувати чисельні методи інтегрування, що збільшує витрати машинного часу на одержання кожного випадкового числа; навіть для випадків, коли інтеграл (5.4) береться в кінцевому вигляді, виходять формули, що містять операції логарифмування, добування кореня й т.д., які реалізуються в ЕОМ шляхом розкладання, що також різко збільшує витрати машинного часу на одержання кожного випадкового числа.
Серед наближених методів (способів) виділяють універсальні (за допомогою яких можна одержувати випадкові числа із законом розподілу будьякого вигляду) та неуніверсальні (придатні для одержання випадкових чисел з конкретним законом розподілу).
Серед наближених виділяється універсальний метод одержання випадкових чисел, заснований на кусковій апроксимації функції щільності. Нехай потрібно одержати послідовність випадкових чисел { yi } з функцією щільності fη( y ) , можливі значення якої лежать в інтервалі (а, b). Подамо
fη( y ) у вигляді кусково-постійної функції, тобто розіб’ємо інтервал (а, b) на
mінтервалів (рис. 5.6). Тоді випадкову величину η можна надати у вигляді
η= ak + η* , де ak – абсциса лівої границі k-го інтервалу; η* – випадкова величина, можливі значення якої розташовуються рівномірно всередині k-го
69
