
2-Konspekt_lektsiy_MS
.pdf
інтервалу. Доцільно розбити (а, b) на інтервали так, щоб імовірність попадання випадкової величини у будь-який із інтервалів (аk, аk+1 ) була постійною та не
ak +1
залежала від номера інтервалу k: ∫fη( y ) dy = 1 / m .
ak
Рисунок 5.6 – Кусково-постійна апроксимація функції щільності fη( y )
Алгоритм реалізації цього способу зводиться до послідовного виконання таких дій:
–генерація випадкового числа хі з інтервалу (0, 1);
–вибір випадковим чином інтервалу (аk, аk+1 ) на основі числа хі (наприклад, методом жеребкування);
–генерація числа хі+1 і масштабування його до інтервалу (аk, аk+1 )
шляхом помноження на ( ak+1 − ak );
– обчислення випадкового числа yi = ak +( ak +1 - ak )xi +1 з необхідним законом розподілу.
Серед неуніверсальних найбільшого поширення на практиці набув спосіб перетворення послідовності рівномірно розподілених випадкових чисел { xi } у послідовність із заданим законом розподілу { yi } на основі граничних теорем теорії ймовірностей.
Нехай потрібно одержати послідовність випадкових чисел { yi }, що мають нормальний розподіл з математичним сподіванням а і середнім квадратичним відхиленням σ. Застосуємо центральну граничну теорему: якщо незалежні однаково розподілені випадкові величини ξ1, ξ2 ,...,ξN мають кожна математичне очікування а1 і середнє квадратичне відхилення σ1 , то їх сума
N
∑ξi асимптотично нормальна з математичним сподіванням а = N а1 і середнім
i =1
квадратичним відхиленням σ = σ1  N .
N .
70
Виходячи з цього, можна формувати випадкові числа { yi } у вигляді сум послідовностей випадкових чисел { xi }, що мають рівномірний розподіл в
N
інтервалі (0,1). Як показують розрахунки, ∑ξi має розподіл, близький до
i =1
нормального, уже при порівняно невеликих N = 10 – 12.
5.4 Особливості фіксації результатів статистичного моделювання При виборі способів фіксації та методів обробки результатів
статистичного моделювання необхідно враховувати такі особливості машинних експериментів з моделями систем.
1.Можливість отримувати при моделюванні системи S на ЕОМ великих вибірок дозволяє кількісно оцінити характеристики процесу функціонування системи, але перетворює в серйозну проблему зберігання проміжних результатів моделювання. Виходом є використання рекурентних алгоритмів обробки, коли оцінки обчислюють по ходу моделювання, причому великий обсяг вибірки дає можливість користуватися при цьому досить простими асимптотичними формулами.
2.Складність більшості досліджуваних систем при їх моделюванні на ЕОМ часто призводить до того, що апріорне судження щодо характеристик процесу їх функціонування, наприклад щодо типу очікуваного розподілу вихідних змінних, є неможливим. Виходом є використання непараметричних оцінок та оцінок моментів розподілів.
3. Блочність конструкцій машинних моделей M M і роздільне дослідження блоків пов’язані з програмною імітацією вхідних змінних для однієї часткової моделі за оцінками вихідних змінних, отриманих на іншій частковій моделі. Якщо ЕОМ, що використовується для моделювання, не дозволяє скористатися в повному обсязі отриманою інформацією, то можна подати відповідні змінні у формі, зручній для побудови алгоритму їх імітації.
|
|
Розглянемо найзручніші для програмної реалізації методи оцінки |
||||||||
розподілів та |
деяких їх |
моментів |
при достатньо |
великому обсязі |
вибірки |
|||||
(кількості реалізацій N). |
|
|
|
|
|
|
|
|||
|
|
Математичне сподівання та дисперсія випадкової величини ξ відповідно |
||||||||
мають вигляд: |
|
|
|
|
|
|
|
|
||
μ |
ξ |
= M [ξ ] = |
∞ x f ( x ) dx ; |
σ 2 = D[ξ ] = M [( x − μ |
ξ |
)2 ] = ∞( x − μ |
ξ |
)2 |
f ( x ) dx , |
|
|
|
∫ |
ξ |
|
∫ |
|
|
|||
|
|
−∞ |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
71 |
|
|
|
|
|
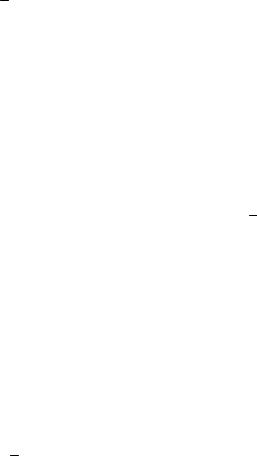
де f ( x ) – щільність розподілу випадкової величини ξ , що набуває значення х.
Під час проведення імітаційного експерименту зі стохастичною моделлю системи S визначити ці моменти не можна, тому що щільність розподілу, як правило, апріорі невідома. Тому при обробці результатів моделювання доводиться задовольнятися лише деякими оцінками моментів, отриманими на кінцевому числі реалізацій N. При незалежних спостереженнях значень
випадкової величини |
ξ як такі оцінки використовуються вибіркові середнє та |
|||||||
дисперсія |
|
|
|
|
|
|
|
|
~ |
N |
2 |
2 |
N |
2 |
|
|
|
= ( 1 / N )∑xi ; |
] =( 1 / N )∑ |
, |
(5.5) |
|||||
x = μξ |
Sb |
= [σξ |
( xi − x ) |
|||||
|
i =1 |
|
|
i=1 |
|
|
|
|
де x – вибіркове середнє; Sb2 – вибіркова дисперсія.
З великою кількістю реалізацій N (як результат моделювання на ЕОМ) отримують значний обсяг інформації щодо стану процесу функціонування системи. Тому необхідно раціонально організовувати фіксацію і обробку результатів моделювання, щоб оцінки характеристик формувалися поступово по ходу моделювання (без спеціального запам’ятовування всієї інформації щодо станів системи).
Для оцінки середнього значення x випадкової величини ξ відповідно до (5.5) необхідно зберігати лише суму значень випадкової величини, яких вона набуває при різних реалізаціях та значення кількості реалізацій N .
За оцінку ймовірності настання події можна використовувати вибіркове значення частоти її настання p = n / N (де n – кількість випадків настання події), що потребує зберігання лише значення n та N .
За оцінку дисперсії випадкової величини ξ під час обробки результатів моделювання можна використовувати формулу (5.5). Безпосереднє обчислення дисперсії за цією формулою є нераціональним, у зв’язку з тим, що середнє значення x змінюється в процесі накопичення значень xi . Це призводить до необхідності зберігання всіх N значень xi . Більш раціонально організувати фіксацію результатів моделювання для оцінки дисперсії з використанням простішої формули
72
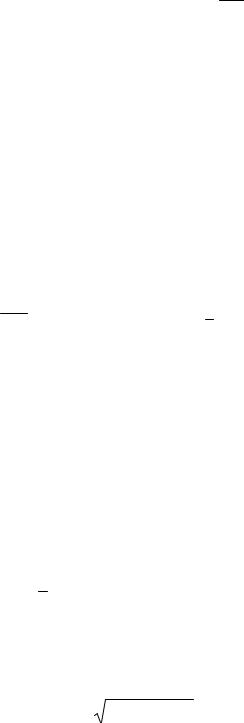
Sb2 |
|
N |
N |
|
=σξ2 |
] =1 /( N −1)[ ∑xi2 |
−(1/N )(∑x )2 ] . |
(5.6) |
|
|
|
i=1 |
i=1 |
|
Для обчислення за формулою (5.6) необхідно зберігати лише значення суми квадратів та квадрату суми значень випадкової величини.
При оцінці ймовірностей можливих значень випадкової величини (закону розподілу) область можливих значень випадкової величини ξ розбивається на m інтервалів. По ходу експериментів накопичується кількість попадань випадкової величини в кожен з інтервалів nk , k = 1,m . Оцінкою для ймовірності потрапляння випадкової величини в інтервал з номером k служить величина pk = nk / N . При цьому достатньо фіксувати m значень nk та значення кількості реалізацій N .
5.5 Оцінка точності результатів статистичного моделювання
Для забезпечення статистичної стійкості результатів, які отримують методом статистичного моделювання, відповідні оцінки обчислюють на основі великої кількості реалізацій N .
Нехай як оцінка деякого параметра a , що визначається за результатами
моделювання xi , i = 1,N , обрана величина x . Точність (похибка) оцінки визначається за співвідношенням: ε =| a x |. Ймовірність α того, що похибка ε не перевищить задане значення ε* , розглядається як достовірність оцінки
p[| a − x |≤ε*] =α .
Для ефективного управління процесом моделювання необхідно встановити залежність між точністю та достовірністю результатів і кількістю реалізацій N , за якими вони визначаються.
Нехай метою статистичного експерименту з моделлю M M деякої системи
S є визначення оцінки |
p |
ймовірності появи |
події p = p( A ). |
Як оцінку |
ймовірності використовують частоту появи події |
p = n / N , де n |
– кількість |
||
випадків настання події A . Тоді похибка оцінки |
|
|
||
|
|
ε = tα p( 1 − p ) N , |
|
(5.7) |
73 |
|
|
||
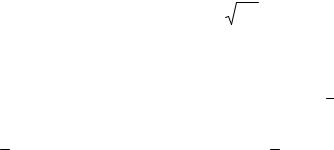
де tα – табличний параметр (квантиль нормального розподілу ймовірностей).
Із (5.7) можна визначити кількість реалізацій, необхідних для отримання
оцінки a з точністю ε і достовірністю α |
|
N = t2 p( 1 − p ) / ε2 . |
(5.8) |
α |
|
Якщо, як оцінка математичного очікування використовується середнє
N
арифметичне x = ( 1 / N )∑xi , формули для оцінки похибки і необхідної
i =1
кількості експериментів матимуть вигляд
ε = tασ / N ; |
(5.9) |
N = tα2σ2 / ε2 , |
(5.10) |
де σ – середньоквадратичне відхилення оцінки x .
Якщо за результатами статистичного моделювання здійснюється оцінка і ймовірності p , і математичного очікування x , використовують обидві пари формул (5.7) – (5.8) і (5.9) – (5.10) та обирають для кількості реалізацій більше з отриманих значень.
Контрольні запитання та завдання
1.Опишіть роботу алгоритму, побудованого за часовим принципом.
2.Які переваги мають алгоритми, побудовані за подійним принципом?
3.Як змінюється значення лічильника часу в алгоритмах, побудованих за принципом послідовного проведення заявок?
4.Назвіть основні форми подання моделювальних алгоритмів.
5.Що служить теоретичною основою методу статистичного моделювання.
6.Наведіть схему методу статистичного моделювання.
7.Розробіть моделювальний алгоритм для дослідження розглянутої вище стохастичної системи.
8.Опишіть алгоритм визначення оцінки площі фігури методом
74
статистичного моделювання.
9.Опишіть способи генерації випадкових чисел. Назвіть їх переваги та недоліки.
10.Який спосіб генерації випадкових чисел найчастіше використовується при статистичному моделюванні КСУА?
11.Опишіть суть процедури генерації випадкових чисел, побудованої на основі конгруентного методу.
12.У чому суть імітації випадкових подій за жеребом?
13.Опишіть алгоритм одержання випадкових чисел, заснований на кусковій апроксимації функції щільності.
14.Який з методів генерації випадкових величин із заданим законом розподілу є найточнішим?
15.Назвіть особливості машинних експериментів з моделями систем.
16.Запишіть співвідношення для оцінки вибіркових значень середнього, частоти, дисперсії.
17.Запишіть співвідношення для визначення точності оцінок за результатами статистичного моделювання.
18.Запишіть співвідношення для визначення необхідної кількості реалізацій N.
6АНАЛІТИЧНЕ МОДЕЛЮВАННЯ ДИНАМІКИ ОБ’ЄКТІВ
6.1Диференціальні моделі керованих об’єктів
Більшість моделей, що описують динаміку керованих об’єктів, є диференціальними, тобто являють собою диференціальні рівняння та їх системи. Серед диференційних моделей розрізняють: моделі у змінних входивиходи та моделі у змінних стану.
Опис об’єктів у змінних входи-виходи має вигляд:
y = Hu, |
(6.1) |
де y – вектор вихідних (керованих) змінних розмірністю m ×1; H – деякий оператор;
u – вектор вхідних змінних (змінних збурення і управління) розмірністю
l×1.
75

У залежності від виду рівняння до складу оператора H у (6.1) можуть входити операції алгебраїчних чи функціональних перетворень, диференціювання, інтегрування, визначення кінцевих різниць і т.п. В окремому випадку для лінійних стаціонарних об’єктів оператор H являє собою матрицю передаточних функцій (передаточну матрицю).
Нехай вихідна yi і вхідна uj змінні зв’язані диференціальним рівнянням з постійними коефіцієнтами:
|
d |
|
l |
d |
|
|
|
Ni ( |
)yi |
= ∑M j ( |
|
) u j , і=1, 2,…, т, |
(6.2) |
||
|
dt |
|
|||||
|
dt |
j =1 |
|
|
|
||
де Ni, Mj – поліноми степенів ni та mj |
відповідно, при чому ni ≥mj; |
|
|||||
yi(t) – вихідна змінна, яка визначається із рівняння (6.2) для заданих |
|||||||
початкових умов yi ( 0 ), yi′( 0 ),..., |
yi( ni −1 )( 0 ) ; |
|
|||||
uj(t) – функція, для якої права частина рівняння (6.2) має сенс. |
|
||||||
Якщо замінити у (6.2) символ диференціювання dtd на комплексну змінну p і ввести передаточну від uj(t) до yi(t) функцію виду:
W ( p ) = |
M j ( p ) |
, |
(6.3) |
|
|
|
|||
ij |
Ni ( p ) |
|
|
|
|
|
|
||
то рівняння (6.2) з урахуванням (6.3) можна записати у вигляді:
l
yi = ∑Wij ( p ) u j , i =1, 2,..., m , (6.4)
j =1
або у матричній формі:
y =W( p )u , |
(6.5) |
де W(p) – матриця передаточних функцій розмірності m×l, елементами якої є передаточні функції Wij(p).
При нульових початкових умовах і t=0 передаточна функція лінійної системи з постійними коефіцієнтами дорівнює відношенню перетворень
76
Лапласа ~i
y ( s )
~ |
|
|
|
|
|
|
та u j ( s ) відповідно вихідної yi(t) та вхідної uj(t) змінних: |
||||||
|
|
|
|
∞ |
|
|
|
~ |
|
|
∫ yi ( t ) e−st dt |
|
|
W ( s ) = |
yi ( s ) |
|
= |
0 |
. |
|
~ |
∞ |
|||||
ij |
|
|
|
|||
|
u j ( s ) |
|
∫u j ( t ) e−st dt |
|
||
|
|
|
|
0 |
|
|
Подання об’єктів у змінних входи-виходи (6.1) – (6.5) дає можливість досліднику мати справу з фізичними змінними не тільки у кінцевому результаті, але й на проміжних етапах. Однак при цьому описи різних навіть лінійних систем і блоків можуть суттєво відрізнятись.
Опис об’єктів у змінних стану. Введемо в (6.1) замість деяких (або усіх) вихідних змінних y інші змінні x, які будемо називати змінними стану. Тоді опис об’єктів у змінних стану може бути поданий у формі Коші, тобто у вигляді системи диференціальних рівнянь першого порядку, розв’язаних відносно похідних:
x = f ( x,u,t ), |
(6.6) |
де x=[x1, x2,…, xn] – вектор станів, компоненти x1, x2,…, xn – змінні стану. Рівняння (6.6) і (6.1) повинні бути еквівалентними у тому сенсі, що знаючи розв’язок одного з них, можна однозначно отримати розв’язок другого. Для цього змінні x і y повинні, перед усім, бути зв’язані однозначною
функціональною залежністю:
y =ϕ( x,u ) , |
(6.7) |
а також виконуватись умови існування розв’язку та (для багатьох практичних задач) його єдиності.
Рівняння (6.6) і (6.7) у матричній формі матимуть вигляд:
– для нестаціонарних об’єктів x = A(t)x + B(t)u; y = C(t)x + D(t)u;
– для стаціонарних лінійних об’єктів x = Ax + Bu; |
y = Cx + Du, |
де x Rn ; y Rm ; u Rl , а матриці A, B, C i |
D мають відповідно |
розмірність n ×n , n ×l , m×n , m×l .
Моделі у змінних стану більш одноманітні і зручні за формою.
77
6.2 Приклади моделей динаміки керованих об’єктів
Приклад 1. Модель управління запасами. Нехай мається деякий запас
розміром |
x( t ), який витрачається зі |
швидкістю y( t ) і |
поповнюється зі |
|||
швидкістю u( t ). Швидкість зміни запасу: |
|
|
||||
|
|
dx( t ) |
= u( t ) − y( t ). |
|
(6.8) |
|
|
|
|
|
|||
|
|
dt |
|
|
|
|
Темп |
витрат запасу |
y( t ) не підлягає управлінню. |
Закон |
управління |
||
повинен забезпечувати заданий постійний рівень запасу x( t ) = a >0 |
для будь- |
|||||
якого темпу витрат y( t ) . |
|
|
|
|
|
|
Таким умовам задовольняє такий закон управління: |
|
|
||||
|
y − k( x − a ), якщо y − k( x − a ) ≥0; |
|
(6.9) |
|||
|
u( t ) = |
|
|
− a ) <0, |
|
|
|
0, якщо y − k( x |
|
|
|||
де k – деяка додатна постійна. |
|
|
|
|||
Зважаючи на те, що |
управління |
ведеться тільки при x( t ) < a , та з |
||||
урахуванням того, що y( t ) ≥0 , модель закону управління для системи (6.8) – (6.9) може бути подана таким рівнянням:
u( t ) = −k( x − a ).
Приклад 2. Навігаційна задача швидкодії. Судно у момент часу t = t0
знаходиться у точці А(0) з координатами ( x1( 0 ) , x2( 0 ) ). Знайти такий курс судна
ϕ , на якому воно досягне заданої кінцевої точки t = t1 за найменший час:
t!
T = t1 −t0 = ∫dt → min .
t0
A( 1 )( x1( 1 ) , x(21 ) ) у момент
(6.10)
Якщо допустити, що судно має постійну швидкість v = const , а течія
78
(збурення) – постійну швидкість |
s = const , вектор якої співпадає з напрямком |
||||||||||
x1, то рівняння кінематики судна можна подати у такому вигляді: |
|||||||||||
|
|
|
dx1 |
= s + v cos ϕ ; |
|
dx2 |
= v sin ϕ , |
||||
|
|
|
|
|
|
||||||
|
|
|
dt |
|
|
dt |
|
|
|||
або |
dx1 |
= s + v u1 ; |
|
dx2 |
= v u2 , |
де u1 , |
u2 |
– управляючі параметри, значення |
|||
|
|
||||||||||
|
dt |
|
dt |
|
|
|
|
|
|||
яких повинні задовольняти умові: |
|
|
|
|
|
||||||
|
|
|
|
|
|
u12 + u22 =1. |
(6.11) |
||||
Таким чином, задача зводиться до вибору таких управляючих сигналів u1o
і u2o із області (6.11), які мінімізують значення часу (6.10).
6.3 Перетворення моделей динаміки
На практиці використовують різні математичні форми моделей динаміки керованих об’єктів, як з точки зору порядків систем рівнянь, так і з точки зору форми їх подання. З урахуванням специфіки задач моделювання і того, що методи аналізу моделей орієнтовані на деякі канонічні форми, виникає необхідність їх перетворення.
Перетворення моделей у змінних стану до форми Коші. Нехай динаміка досліджуваного об’єкта описується системою звичайних диференціальних рівнянь такого виду:
x = a′xx x + axx x + a′xy y + axy y + axz z + axδδ + fx ; |
|
y = a′yx x + ayx x + a′yy y + ayy y + ayz z + ayδδ + f y ; |
(6.12) |
z − a′zz z + azz z = azx x + azy y,
де x, y, z – змінні моделі, які характеризують стан об'єкта; aij – постійні коефіцієнти, і = x, y, z, j = x, y, z, δ;
δ – функція часу керуючого впливу; fх, fу – функції збурення.
79
