2-Konspekt_lektsiy_MS

–вибір методу ідентифікації та розробка алгоритмів оцінки параметрів об’єкта q ;

–перевірка адекватності отриманої моделі об’єкта.

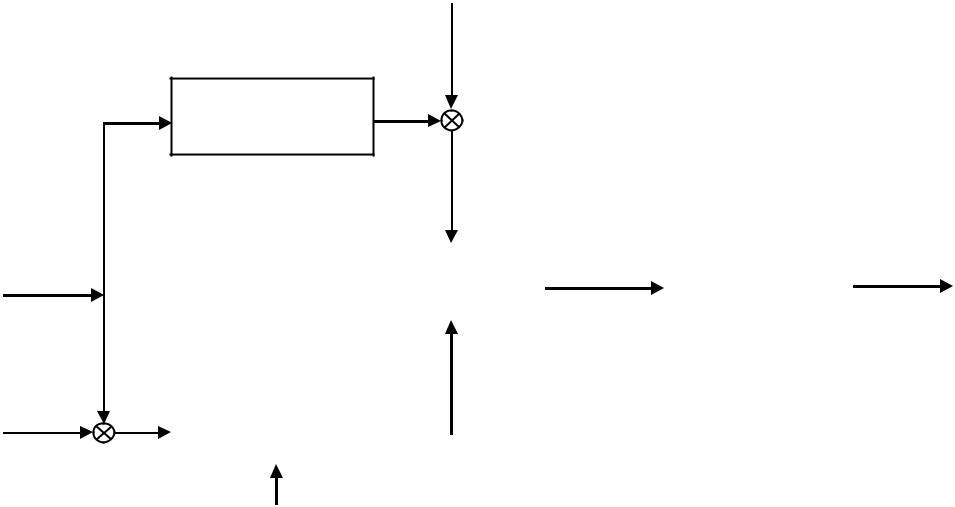
Процес параметричної ідентифікації здійснюється таким способом (рис. 2.3). На вхід об’єкта подається відомий сигнал u(t). Цей же сигнал подається на вхід моделі, але через завади ηM ( t ), вхідний сигнал моделі uM ( t ) є комбінацією u(t) и ηM ( t ). Оператор об’єкта F [ u, q,η] характеризується своєю структурою та m -вимірним вектором параметрів q . Модельний оператор об’єкта FM характеризується структурою, m -вимірним вектором qM параметрів і вектором похибок ηM ( t ). Приведена до виходу об’єкта похибка η(t) складається з двох частин η1 (t) – похибка вимірювання та η2 (t) – похибка неточності задання моделі або неточності визначення оператора об’єкта. Похибка η2 (t) частіше за все виникає через надмірне спрощення моделі.

Ефективність ідентифікації визначається критерієм подібності об’єкта і моделі K , який досягає глобального екстремуму у випадку еквівалентності F( t ) і FM ( t ) . Критерій K прийнято формувати як функцію (функціонал) від

де ΩM , QM – відповідно множини допустимих операторів і значень параметрів моделі.

Вичерпною характеристикою динамічних об’єктів є власні значення їх операторів (власні частоти об’єктів). У зв’язку з цим для забезпечення умов ідентифікованості необхідно: щоб вхідний сигнал об’єкта u(t) збуджував усі коливання, що відповідають власним частотам об’єкта, а вихідний сигнал y( t ) містив достатньо інформації щодо власних частот об’єкта. Перша умова є умовою керованості об’єкта, а друга – умовою спостережуваності.

Методи розв’язання задач ідентифікації розрізнюють: за виглядом моделей (функціональної ідентифікації – для об’єктів типу «чорний ящик» та параметричної ідентифікації – для об’єктів типу «сірий ящик»); за характером об’єктів, що ідентифікуються (лінійних і нелінійних, статичних і динамічних, одновимірних і багатовимірних, неперервних і дискретних об’єктів); за способом одержання інформації (пасивної та активної ідентифікації); за

21

Ідентифікація за методом найменших квадратів. Вихід моделі yM ( t )

формується на основі відомостей щодо класу функцій FM ( t ) , серед яких необхідно визначати найкращу модель. Це потребує знання аналітичного опису моделі з точністю до скінченої кількості числа параметрів, що робить можливим використання різних методів оцінки і прийняття рішень. Частіше за все під час розв’язання задач ідентифікації використовують методи (за назвою критеріїв (2.19)) найменших квадратів, найменших зважених квадратів.

Нехай об’єкт моделювання типу «сірий ящик» є статичним, а його модель має вигляд:

де yM(t) – вихідний сигнал моделі; FM – оператор моделі;

uM(t) – вхідний сигнал моделі; qM – вектор параметрів моделі;

ηM ( t ) – вектор завад на вході моделі.

Входи і виходи об’єкта та моделі спостерігаються у дискретні моменти

параметрів за методом найменших квадратів можуть бути визначені шляхом мінімізації критерію:

де QM – множина допустимих значень параметрів моделі.

Наведений критерій передбачає однакову важливість (точність) спостережень на всьому інтервалі [t1, tп]. За наявності додаткової інформації щодо важливості спостережень у кожний із моментів часу t1, t2, …, tп кращих результатів можна досягнути, використовуючи критерій найменших зважених квадратів:

×{ y( t j ) − Fm [ uM ( t j ), qM ,ηM ( t j )] } → min ,

qM QM

де RRij – елемент коваріаційної матриці, що враховує відносну вагу

23

похибок вимірювань сигналів у моменти часу ti та t j .

З математичної точки зору задача параметричної ідентифікації зводиться до визначення оцінок параметрів qMo , значення яких мінімізують критерії (2.21) або (2.22). У багатьох випадках розв’язки вдається визначити безпосередньо, розв’язуючи системи нормальних рівнянь виду:

Наприклад, нехай об’єктом дослідження є одновимірна система типу "сірий ящик", об’єкт знаходиться у стані вільного руху (на вході об’єкта відсутні сигнали, тобто u(t) = t), а модель визначена як поліном ступеня k:

Тоді за критерієм найменших квадратів (2.21) оптимальні значення параметрів з умови (2.23) визначатимуться як розв’язки системи лінійних алгебраїчних рівнянь:

де n – кількість сигналів, що спостерігаються (експериментів).

У загальному випадку для розв’язання задачі параметричної ідентифікації використовуються обчислювальні методи мінімізації функцій подібності об’єкта і моделі (2.19).

Контрольні запитання та завдання

1.За якими ознаками здійснюється класифікація видів моделювання?

2.Дайте визначення математичного моделювання.

3. У чому полягає відмінність аналітичного моделювання від

24

імітаційного?

4.Які переваги має імітаційне моделювання перед аналітичним?

5.Як визначається ефективність моделювання?

6.Які вимоги висуваються до математичних моделей?

7.Дайте визначення показників якості моделей.

8.Наведіть співвідношення для визначення стійкості розв’язків для моделей у вигляді систем лінійних алгебраїчних рівнянь.

9.Назвіть основні етапи моделювання систем.

10.У чому проявляється ітераційність процесу моделювання?

11.Що розуміють під формалізацією опису об’єктів моделювання?

12.Чим визначається множина властивостей об’єкта?

13.Сформулюйте задачі інженерного синтезу систем.

14.Дайте визначення поняття "ідентифікація об’єкта".

15.Які задачі розв’язуються у процесі ідентифікації об’єктів?

16.Дайте визначення структурної та параметричної ідентифікації.

17.За якими критеріями розв’язуються задачі ідентифікації?

18.Запишіть критерії найменших та найменших зважених квадратів.

3 МОДЕЛЮВАННЯ ПРОЦЕСІВ ПРИЙНЯТТЯ РІШЕНЬ

3.1 Проблема багатокритеріальної оптимізації

Задачі прийняття рішень традиційно формалізуються в термінах «умови – мета». При цьому «умови» розглядаються як множина станів об’єкта й операторів, що переводять його з одного стану в інший, а «мета» – як бажаний стан об’єкта. Формально задача полягає у виборі альтернативи x X , що призводить до деякого наслідку (результату) u U (U – множина можливих наслідків). Ефективність рішення (розв’язку) визначається ступенем відповідності отриманого наслідку u U поставленій меті й оцінюється за множиною показників (критеріїв).

Основними класами задач прийняття рішень є:

–задача в умовах визначеності – коли кожна альтернатива x X

призводить до єдиного наслідку u U , тобто існує детермінована залежність наслідків від альтернатив;

–задача в умовах ризику – коли кожна з альтернатив x X може призводити до одного з декількох наслідків u U x з певною ймовірністю;

–задача в умовах невизначеності – коли кожна з альтернатив x X може

25

призводити до одного з декількох наслідків u U x , причому відсутня навіть стохастична залежність наслідків від альтернатив.

У процесі розв’язання проблема прийняття рішень розглядається як система Pr:

де Tasks – множина задач;

Rels – множина відношень між задачами, що визначають схему їхніх взаємозв’язків за вхідними і вихідним даними;

Task6 – задача вибору екстремальної альтернативи xo X K .

Задача формалізації мети Task1 у найпростішому випадку полягає у

критеріїв) ефективності k1( x ), k2 ( x ),..., km ( x ). При цьому часткові критерії ki ( x ), i = 1, m , як правило, мають різний фізичний зміст, розмірність, інтервали вимірювання і є суперечливими.

Розв’язання задачі визначення універсальної множини альтернатив X U (Task2 ) здійснюється виходячи зі специфіки задачі або ситуації прийняття рішення.

Задача визначення множини допустимих альтернатив X X U (Task3 )

полягає у вилученні з універсальної множини X U підмножини варіантів X , які не задовольняють обмеження розв’язуваної задачі X = X U \ X . Задля цього потрібно визначати функціональні та вартісні характеристики варіантів x X U .

26

Основними засобами оцінки локальних властивостей k j ( x ) , j = 1, m варіантів

x X U є аналітичне й імітаційне комп’ютерне моделювання. Для одержання узагальнених оцінок якості варіантів P(x) використовуються методи експертного і багатофакторного оцінювання на основі функцій корисності часткових критеріїв (ФКЧК).

Задача виділення підмножини ефективних альтернатив X K X (Task4 ) полягає у вилученні з множини допустимих неефективних (неоптимальних) альтернатив X C , що належать до множини згоди. Розв’язок називають ефективним xo X (Парето-оптимальним, таким, що не може бути покращеним), якщо не існує більш кращого розв’язку x X , тобто xo x для всіх x X .

Розв’язання задачі ранжирування альтернатив Task5 здійснюється на основі парадигми максимізації корисності. Для її розв’язання використовуються два підходи: упорядкування варіантів особою, яка приймає рішення (ОПР) або формування узагальненого критерію ефективності й зведення задачі до задачі багатофакторного оцінювання. При цьому в обох підходах вважається, що кожному з варіантів із множини допустимих (або ефективних) x X приписується деяка корисність (цінність) P( x ), значення якої й визначають порядок:

x, y X : x ~ y ↔ P( x )= P( y );

xy ↔ P( x )> P( y );

x~ y ↔ P( x )≥P( y ) .

Порядок альтернатив може визначатися на основі ординальної (порядкової) та кардинальної (кількісної) теорії корисності.

Задача вибору найкращої альтернативи xo X K (Task6 ) у наведених вище умовах зводиться до вибору крайнього елемента впорядкованого ряду розв’язків або до безпосередньої екстремізації функції узагальненої корисності

(ФУК):

x X K

методами математичного програмування. 27

Процеси прийняття рішень, крім перерахованих, можуть включати інші задачі, що пов’язані зі специфікою проблемної ситуації, об’єкта проектування або керування, використовуваної методології. При цьому кожна із задач, у свою чергу, за необхідності може бути розбита на ряд взаємозалежних підзадач.

Схема вирішення проблеми багатокритеріального вибору в межах кардиналістичного підходу подається в такий спосіб:

де S – ситуація прийняття рішення;

A – аксіоматика прийняття рішення, що являє собою набір аксіом, які визначають схему компромісу (принцип упорядкування рішень);

оpt Θ – схема компромісу (узагальнений критерій, ФУК); xo – ефективний розв’язок.

Плідним для вирішення цієї проблеми виявляється застосування аналітико-евристичного підходу, що полягає у виборі ОПР аксіоматики А, на основі евристичних міркувань.

3.2 Бінарні відношення між альтернативними варіантами

Найважливішою серед виділених, з методологічної точки зору, вважається задача ранжирування альтернатив x X K (Task5 ). Її розв’язання передбачає вибір принципу оптимальності П й синтез на його основі функції вибору CΠ , що визначає метрику для ранжирування альтернатив P( x ). Вибір виду P( x ) являє, по суті, розв’язання задачі ідентифікації. При цьому найбільший інтерес, як у теоретичному, так і в практичному плані становляють питання вибору структури і параметрів моделі P( x ).

Для формалізації процедури вибору ефективних розв’язків ОПР використовується апарат бінарних відношень. Бінарним відношенням R на непустій множині альтернатив Х називають підмножину множини всіх

означає, що (x, y) належить R; аналогічно не x R y ( x R y ) означає, що (x, y) не належить R, або що x не перебуває у відношенні R до y.

У теорії прийняття рішень використовують три види бінарних відношень: 28

x R x для кожного x X;

–симетричним, якщо з x R y випливає y R x; асиметричним, якщо з x R y випливає y R x ;

–транзитивним, якщо з x R y і y R z випливає x R z; негативно

транзитивним, якщо з xR y і y R z випливає x R z ;

– зв’язаним, якщо x R y або y R x; слабко зв’язаним, якщо з x ≠ y випливає x R y або y R x.

Транзитивне бінарне відношення R( X ) називається впорядкуванням або відношенням порядку.

Як наслідок суб’єктивності ОПР на практиці досить часто зустрічаються приклади нетранзитивних переваг. Нехай потрібно вибрати варіант побудови системи управління на множині альтернатив з такими характеристиками:

–x: оперативність –8 с, надійність – 0.95, вартість – $350 тис.;

–y: оперативність – 9 с, надійність – 0.96, вартість – $400 тис.;

–z: оперативність – 10 с, надійність – 0.97, вартість – $450 тис.

ОПР може зволіти x більше, ніж y, розсудивши, що підвищення надійності не коштує втрати оперативності в 1 с і $50 тис. Виходячи з аналогічних міркувань вона воліє y скоріш, ніж z, але порівнюючи х і z , вона воліє z у порівнянні з x, вважаючи, що підвищення надійності в 0.02 важливіше за втрату оперативності в 2 с і $100 тис. В описаній ситуації переваги ОПР утворюють цикл x y, y

29