
Лекции атомная физика
.pdfвідношеннях взаємовиключні, то приходиться заключити, що електрони насправді не є ні тим, ні іншим. Однак, оскільки ми змушені для опису одних і тих же об’єктів користуватися і хвильовою і корпускулярною картинами, ми вже не можемо приписати цим об’єктам всі властивості частинок і всі властивості хвиль. Необхідно внести обмеження у застосуванні до електронів цих картин.
В класичній механіці стан матеріальної частинки в кожний момент часу характеризується її розташуванням і імпульсом. Наявність у електронів хвильових властивостей вносить суттєві обмеження в можливість такого опису стану системи мікрочастинок.
Припустимо, що нам відоме розташування мікрочастинки на осі х з
деякою неточністю х, так, що можна стверджувати, що частинка знаходиться на інтервалі від х до х+ х. Цей факт у хвильовій картині описується, очевидно,
тим, що амплітуда хвильової функції відмінна від нуля лише на ділянці х. Така функція становить собою хвильовий пакет – суперпозицію синусоїдальних хвиль із значеннями хвильового вектора в діапазоні від kx до kx+ kx .
Розглянемо хвильовий пакет, утворений синусоїдами з однаковою амплітудою, хвильові числа яких зростають на одну й ту ж величину. В точці х фази хвиль змінюються від від kxх до (kx+ kx )х, тобто на величину х kx . Якщо
х kx = 2 , то в цій точці всі синусоїди взаємно гасять одна одну. Знайдемо найближчу точку х+ х, в якій буде також відбуватися гасіння. В цій точці різниця фаз між крайніми синусоїдами буде дорівнювати
(kx kx)(x x) kx (x x) x kx x kx 2 x kx .
Найближче гасіння відбудеться, коли х kx 2 . Отже все хвильове змушення розіб’ється на відрізки довжиною х, на кінцях яких хвильове поле обертається в нуль. Якщо скористатися синусоїдами усіляких амплітуд, то можна всилити змушення в границях тільки одного відрізку х, а всюди в інших погасити. Це виходить із теореми Фур’є, причому необхідною умовою є виконання співвідношення:
х kx 2 .
Отже мінімальна ширина інтервалу kx в хвильовому пакеті повинна задовольняти наведеній умові. Домножаючи обидві частини цієї нерівності на
і зважаючи на те, що kx |
px , одержимо (для інших координат аналогічно): |
||
х px 2 |
|
|
|
|
2 |
Нерівності Гейзенберга, 1927 . |
(3.4) |
y py |
|||
|
2 |
|
|
z pz |
|
|
|
31

Із цих співвідношень виходить, що координата х і імпульс рх не можуть одночасно мати визначені значення, тобто якщо х = 0, то рх . Отже чим точніше локалізоване розташування частинки (чим менше х), тим більше невизначеність відповідної складової імпульсу, і навпаки. Таким чином,
принцип невизначеності Гейзенберга відбиває той факт, що в природі об’єктивно не існують стани мікрочастинок із точно визначеними значеннями обох змінних: х і рх.
Співвідношення Гейзенберга проявляється при будь-якій спробі
вимірювання точного розташування або імпульсу частинки.
Приклад 1. Розглянемо експеримент, що дозволяє прямим шляхом визначити швидкість електрона (мал. 3.7). Нехай на екран із щілиною ширини d (діафрагму) падає електрон, що рухається паралельно осі пристрою. Якщо електрон пройшов через щілину, то його координата х буде зафіксована з точністю х ~ d. Звужуючи ширину щілини можна визначити розташування
|
|
|
|
|
|
електрону |
|
з |
необхідною |
|
|
|
|
|
|
точністю. |
Здається, |
імпульс |
|||
|
|
|
|
A |
|
|||||
|
|
|
|
|
|
електрона |
|
також |
є |
цілком |
|
|
|
|
|
|
|
||||
p |
|
|
|
|
|
визначеним. |
Оскільки імпульс |
|||
d |
y |
р паралельний осі у, то рх = 0, |
||||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
а рy = р. Однак при проходжен- |
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
ні щілини |
пласка хвиля де- |
|||
|
|
|
|
Мал. 3.7 |
||||||
|
|
|
|
Бройля, що |
становить |
собою |
||||
|
|
|
|
|
|
|||||
рух вільного електрона, зазнає дифракції. А це означає наступне: уявимо замість одного електрона їх паралельний потік, що проходить через діафрагму паралельно осі у. Тоді на фотопластинці ми отримаємо дифракційну картину, із вигляду якої можна заключити, що деякі електрони змінюють свій напрямок.
Додатковий імпульс електрона, що потрапляє в точку А |
|
|||
px |
psin |
2 |
sin . |
(3.5) |
|
||||
|
|
|
|
|
Якщо враховувати потрапляння електрона в границі тільки головного дифракційного максимуму, то кут буде кутом між віссю у і напрямком до першого дифракційного мінімуму. Із умови мінімуму xsin і
співвідношення (3.5) отримаємо: х px 2 . Якщо врахувати також додаткові максимуми, то маємо: х px n2 , тобто х px 2 . Це і є співвідношення невизначеності.
Проведемо кількісну оцінку. Маса електрона me = 9∙10-31 кг. Нехай необхідно встановити належність електрона визначеному атому. Розмір атома ~
32
10-10 м, отже доцільна точність х ~ 10-11 м. Тоді |
|
|||||
v |
|
|
1,054 10 34 |
1,17 107 |
м/с. |
|
m x |
9,11 10 31 10 11 |
|||||
|
|
|
|
|||
У дослідах Франка і Герца при енергіях порядку 10 еВ швидкість електрона v ≈ 1,87∙106 м/с. Отже в цьому випадку невизначеність швидкості на порядок більше самої швидкості.
Приклад 2. Спостереження поведінки мікрочастинок в камері Вільсона показує, що при достатньо великій енергії частинок спостерігаються суворо прямолінійні траєкторії і ніяких ознак невизначеності імпульсу, що пов’язані із хвильовими властивостями, не виявляється. Для пояснення цього згадаємо, що прямолінійні траєкторії становлять собою гірлянду маленьких краплинок туману. Розміри краплинок ~ 10-6 м, тому в цьому випадку х = 10-6 м і р ~ 10-28 кг∙м/с у випадку електронів.
Так як з іншого боку прямолінійні траєкторії спостерігаються тільки при дуже великих енергіях, то р<< p, і у вказаних границях точності мікрочастинка буде поводитись як сповна класична частинка. Взагалі при дуже великих енергіях хвилі де-Бройля буде дуже малою, і так само, як в оптиці при дуже малих можна застосовувати геометричне наближення, тобто світлові промені, у випадку мікрочастинок можна говорити про визначені траєкторії.
Аналіз наведених і багатьох інших ситуацій, пов'язаних з вимірами, показує, що виміри у квантовій області принципово відрізняються від класичних вимірів. У квантовій фізиці існує природна межа точності вимірів. Вона у самій природі квантових об'єктів і не може бути переборена ніяким удосконалюванням приладів і методів вимірів. Співвідношення Гейзенберга встановлюють одну з таких меж.
Співвідношення невизначеностей є одним з фундаментальних положень квантової механіки. Одного цього співвідношення досить, щоб одержати ряд важливих результатів, зокрема:
1.Неможливий стан, у якому частинка перебувала б у стані спокою.
2.При розгляді руху квантового об'єкта необхідно в багатьох випадках відмовитися від самого поняття класичної траєкторії.
3.Часто втрачає зміст розподіл повної енергії Е квантової частинки на потенціальну U і кінетичну К, тому що потенціальна залежить від координат, а
кінетична – від імпульсу. Ці ж змінні не можуть мати одночасно визначені значення.
33
4.ФІЗИЧНІ ПРИНЦИПИ КВАНТОВОЇ МЕХАНІКИ
4.1.Рівняння Шредінгера
Виявлення хвильових властивостей мікрочастинок показало, що класична механіка неспроможна описати їх поведінку. Нова механіка, що враховувала ці властивості, була створена Шредінгером, Гейзенбергом, Діраком та ін. і
отримала назву квантової механіки.
Основним рівнянням квантової механіки є рівняння Шредінгера. Подібно рівнянням Ньютона в класичній механіці це рівняння не може бути отримане теоретично. Воно є суттєво новим принципом, який не можна вивести логічно із старих принципів, в яких він не міститься. Можна, звичайно, навести деякі міркування, що пояснюють встановлення рівняння Шредінгера (наприклад,
провести розумне узагальнення хвильового рівняння на випадок дебройлевських хвиль), але подібні узагальнення не можуть, звичайно,
слугувати доказом цього рівняння. Справедливість же рівняння Шредінгера, як і будь-якого вихідного положення нової теорії, підтверджується узгодженням з дослідом результатів, що отримуються з його допомогою.
Зауважимо, що рівняння Шредінгера є нерелятивістським постулатом квантової механіки. В релятивістській області використовується рівняння Дірака.
Пласка хвиля де-Бройля Aexp[i kr t ] описує вільний рівномірний рух мікрочастинки. Основна задача квантової механіки – визначення хвильової функції частинки, яка знаходиться в заданому силовому полі. Для розв’язання цієї задачі і слугує рівняння Шредінгера
|
2 |
2 U i |
д |
, |
(4.1) |
2m |
|
||||
|
|
дt |
|
||
де – хвильова функція, 2 – оператор Лапласа, U U(r,t) – потенціаль-
на енергія частинки.
Як виходить із рівняння (4.1) вигляд хвильової функції визначається потенціальною енергією, тобто характером сил, що діють на частинку. Взагалі кажучи U U(r,t). Для стаціонарного силового поля U не залежить явно від часу. В цьому випадку хвильова функція складається із амплітуди (функції, що не залежить від часу) і множника, періодичного за часом (стояча хвиля).
34

Припустимо, що містить час тільки у множнику типу e i t , тоді розпадається на два множники, один з яких залежить тільки від часу, другий – від координат:
(x,y,z,t) е i t (x,y,z).
Підставимо в (4.1): |
|
|
|
|
|
|
|
||
e i t ; |
|
|
|
i e i t , |
|
||||
|
|
|
|
||||||
|
|
|
|
|
|
|
t |
|
|
отже маємо |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
e i t |
U e i t i ( i ) e i t . |
|
|||||
|
|
||||||||
|
2m |
|
|
|
|
|
|
|
|
Приймаючи гіпотезу, що |
аналогічно квантам світла E |
- повна |
|||||||
енергія частинки у стаціонарному стані, отримаємо рівняння |
|
||||||||
|
|
|
|
2m |
(Е U) 0. |
(4.2) |
|||
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Це рівняння називають рівнянням Шредінгера для стаціонарних станів.
Функція U визначається класично, мов би частинка ніякими хвильовими властивостями не володіє.
Повна хвильова функція е i t є періодичним розв’язком. Але хоч рівняння Шредінгера в деяких випадках задовольняється періодичними розв’язками, ніяких реальних хвиль, що розповсюджуються у фізичному середовищі, вони не описують. Хвильову функцію принципово не можна спостерігати – це не фізична величина.
Згідно Борну, хвильовій функції слід надати статистичну (ймовірнісну) інтерпретацію. При розгляданні хвиль де-Бройля ми показали, що поведінка вільного електрона описується пласкою хвилею де-Бройля, але фізичний зміст має тільки квадрат амплітуди (інтенсивність) цієї хвилі, який пропорційний ймовірності виявити частинку в деякому місці простору (густина ймовірності).
Аналогічно цьому, квадрат модуля 2 * для будь-якої точки простору відіграє роль функції розподілу і характеризує густину ймовірності виявити частинку в момент t в об’ємі простору dV з координатами від r до r dr . Відповідна ймовірність
dP |
|
|
|
2 dV . |
(4.3) |
|
|
Для стаціонарних станів
* e i t ei t * *,
35
так що в цьому випадку густина ймовірності від часу не залежить.
Оскільки * ми інтерпретуємо як ймовірність, необхідно нормувати функцію так, щоб ймовірність достовірної події дорівнювала 1, отже умова нормування матиме вигляд
|
|
*dV 1. |
(4.5) |
Це означає, що частинка знаходить де-небудь у просторі.
Перейдемо до аналізу рівняння Шредінгера. За класифікацією це диференціальне рівняння другого порядку. На хвильову функцію, як розв’язок,
що задовольняє рівнянню другого порядку типу Штурма-Ліувілля повинні накладатися наступні умови. Вона повинна бути неперервною і мати неперервну похідну, крім того, повинна бути однозначною і скінченною у всьому просторі, а також задовольняти визначеним граничним умовам, що визначаються виглядом функції U(r).
Ці вимоги приводять до того, що розв’язки хвильових рівнянь існують не при будь-яких, а тільки при деяких значеннях параметра, які отримали назву
власних значень. У даному випадку таким параметром є енергія із власними значеннями Е1, Е2, Е3... . Відповідні цим власним значенням розв’язки хвильового рівняння 1, 2, 3 ... називаються власними функціями. Можливі значення енергії утворюють так званий енергетичний спектр. Далі ми побачимо, що у разі, коли рух частинки не обмежений у просторі, то її енергетичний спектр неперервний, якщо обмежений – то дискретний.
Отже Шредінгер вирішив проблему квантування енергії системи. Зокрема для атома водню власні значення Е, як ми покажемо пізніше, співпадають із тими, що дає теорія Бора. Знаходження власних значень і власних функцій становить досить складну задачу. В подальшому ми розглянемо деякі найбільш важливіші в атомній фізиці випадки руху.
4.2.Операторний метод
Вбільшості побудувань квантової механіки широко використовується операторний метод. Під оператором розуміють символ, який при дії на функцію деяких змінних дає нову функцію тих же змінних. Символічно це записується наступним чином:
f Qˆ ,
де Qˆ – символічна позначка оператора.
36

Під символом оператора ховається сукупність дій, за допомогою яких вихідна функція перетворюється в іншу функцію f. Наприклад, під символом оператора Лапласа розуміється операція
2 |
2 |
|
2 |
|
2 |
|
x2 |
y2 |
z2 |
||||
|
|
|
над деякою функцією . Зокрема оператор може визначати добуток вихідної функції на деяку функцію Q. Тоді f Qˆ Q і, відповідно, Qˆ = Q.
Звернемося до стаціонарного рівняння Шредінгера (4.2). Введемо оператор Hˆ , який називають оператором Гамільтона або гамільтоніаном:
Hˆ |
2 |
(4.6) |
U . |
2m
Тоді рівнянню Шредінгера можна надати вигляду |
|
Hˆ E . |
(4.7) |
Розглянемо елементи алгебри операторів.
1.Під сумою операторів Aˆ Bˆ розуміють такий оператор, дія якого на будь-яку функцію f(x) дає результат Aˆf(x) Bˆf(x) .
2.Під добутком операторів Aˆ Bˆ розуміють такий оператор, дія якого на будь-яку функцію f(x) дорівнює Aˆ[Bˆf(x)] (спочатку виконується Bˆ , потім Aˆ ).
Частковий випадок добутку – добуток оператора Aˆ на число , тобто Aˆ або
Aˆ .
3. В алгебрі операторів не завжди виконується комутативний закон відносно добутку. Це означає, що не завжди Aˆ Bˆ Bˆ Аˆ . Якщо ця рівність виконується, то говорять, що оператори Aˆ і Bˆ комутують один з одним, якщо ні – не комутують.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Наприклад, не комутують |
x |
|
|
і |
|
|
x : |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|||
|
|
f |
, |
|
|
|
|
|
|
(xf ) |
|
f |
. |
|||
x |
|
f x |
|
|
|
|
|
|
x f |
|
f |
|
||||
|
x |
|
|
|
|
x |
x |
|||||||||
|
x |
|
|
|
x |
|
|
|
|
|||||||
4.Оператор Aˆ називається лінійним, якщо для будь-яких двох функцій f і
і будь яких сталих і виконується співвідношення
Aˆ( f ) Aˆf Aˆ .
В квантовій механіці застосовуються тільки лінійні оператори.
37
Повернемося до рівняння Шредінгера (4.7). Специфіка його в тому, що оператор Hˆ , діючи на хвильову функцію , відтворює її с точністю до
довільного множника Е. Ясно, що це не може бути справедливим для довільної функції і довільного числа Е.
В алгебрі операторів вважається, що у разі виконання умови Fˆf f
величина становить собою власне значення оператора Fˆ , що належить до власної функції f цього оператора.
Таким чином, рівняння Шредінгера можна трактувати як рівняння для визначення власних значень і власних функцій оператора Hˆ . Величина Е становить собою усілякі значення енергії частинки (електрона) в силовому полі
U(r), отже можна вважати, що можливі значення енергії суть власні значення
оператора Hˆ . На цій підставі оператор Hˆ називається ще оператором енергії. Сукупність власних значень оператора енергії утворює спектр припустимих значень енергії частинки. В цьому і полягає принцип квантування
енергії частинки, що рухається в будь-якому силовому полі.
Таке зіставлення проводиться не тільки для енергії, а і для інших фізичних величин: кожній фізичній величині зіставляється оператор, сукупність
власних значень якого становить спектр припустимих значень цієї величини. В операторі енергії (4.6) другий доданок – потенціальна енергія частинки,
його можна розглядати як оператор потенціальної енергії частинки, тобто
Uˆ U . Тому оператор |
|
|
|
|
|
ˆ |
2 |
(4.8) |
|||
T |
|
|
|||
|
2m |
|
|
|
|
|
|
|
|
p2 |
|
слід розглядати як оператор кінетичної енергії. В класичній механіці T |
|
|
. |
||
|
|||||
|
|
|
|
2m |
|
Зважаючи на відповідність між квантовою і класичною механікою, слід
вважати, що Tˆ тільки множником |
1/2m може |
відрізнятись від |
оператора |
||||||||
квадрату імпульсу |
частинки. |
Звідси pˆ i |
– оператор імпульсу, а, |
||||||||
відповідно, оператори проекцій імпульсу мають вигляд |
|
||||||||||
pˆx |
i |
|
|
pˆy |
i |
|
|
pˆz i |
|
. |
(4.9) |
x |
y |
|
|||||||||
|
|
|
|
|
z |
|
|||||
Зупинимося ще на одному питанні, специфічному тільки для квантової механіки. Нехай Aˆ і Bˆ – два квантовомеханічних оператори, кожному із яких відповідає свій спектр власних значень. Виникає питання: чи завжди існує стан
, в якому величини А і В можуть бути виміряні одночасно?
38
Для відповіді на це питання припустимо, що n – власна функція і Aˆ і Bˆ ,
тобто
|
Aˆ |
n |
A |
n |
, |
|
Bˆ |
n |
B |
n |
, |
|
||||
|
|
|
n |
|
|
|
|
|
|
n |
|
|
||||
де A , B – числа, які є власними значеннями операторів Aˆ і Bˆ |
в одному і тому |
|||||||||||||||
n n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ж стані n . Домножаючи першу рівність ліворуч на оператор Bˆ |
отримаємо |
|||||||||||||||
|
ˆ ˆ |
|
ˆ |
|
|
ˆ |
|
|
|
|
|
|
|
|
||
|
BA n |
BAn n |
AnB n AnBn n , |
|
||||||||||||
аналогічно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AˆBˆ |
n |
B A |
n |
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
n n |
|
|
|
|
|
|
|
||
Звідси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(AˆBˆ BˆAˆ) n |
|
0. |
|
|
(4.10) |
||||||
На підставі цього рівняння ще не можна заключити, що AˆBˆ BˆAˆ 0, |
||||||||||||||||
тому що n |
– не довільна функція, а лише одна із спільних власних функцій |
|||||||||||||||
операторів Aˆ |
і Bˆ . Припустимо, однак, що кожна власна функція оператора Aˆ є |
|||||||||||||||
також власною функцією оператора Bˆ |
і навпаки. Існує математична терема, яку |
|||||||||||||||
ми доказувати не будемо, що довільна хвильова функція |
може бути |
|||||||||||||||
розкладена по власних функціях оператора Aˆ |
( або Bˆ ), тобто |
|
||||||||||||||
|
|
|
|
|
n cn n . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
Із цієї формули і співвідношення (4.10) виходить, що |
|
|
|
|||||||||||||
|
|
|
|
(AˆBˆ BˆAˆ) 0. |
|
|
|
|
|
|||||||
Тепер вже, зважаючи на довільність можна заключити: |
|
|||||||||||||||
|
|
|
|
|
AˆBˆ BˆAˆ , |
|
|
|
|
|
|
|
(4.11) |
|||
тобто оператори Aˆ і Bˆ комутативні.
Отже, якщо всі власні функції операторів Aˆ і Bˆ співпадають, то ці оператори комутують. Іншими словами, дві величини А і В можуть бути виміряні одночасно тоді і тільки тоді, коли відповідні їм оператори Aˆ і Bˆ комутують.
4.3. Моделювання потенціальних кривих для визначення
поведінки мікрочастинок
Лише небагато реалістичних квантовомеханічних задач (наприклад, теорія атома водню, гармонічного осцилятора та кілька інших задач)
39
допускають точні розв’язки в аналітичній формі, та й то побудова їх вимагає достатніх математичних знань. У ряді випадків (наприклад, у ядерній фізиці)
дійсний хід потенціальної функції U(х) невідомий. Апроксимуючи в таких випадках U(х) прямокутними бар’єрами і ямами встановлюють не лише загальні особливості поведінки мікрочастинок, а й отримують кількісні результати оціночного характеру.
|
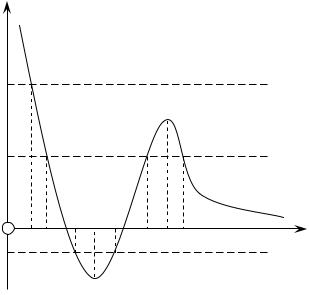
На мал. 4.1 зображений хід потенціальної кривої U(х), яка імітує основні |
||||||||||||
U |
|
|
|
|
й |
характерні |
риси |
потенціальної |
|||||
|
|
|
|
енергії |
|
мікрочастинки |
в |
полі |
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
певного |
|
силового |
центру. |
При |
||||
Е3 |
|
|
|
|
х 0, |
U . |
На |
ділянках |
|||||
|
|
|
|
|
(0, xmin ), |
(x xmax ) |
центр |
відштов- |
|||||
Е2 |
|
|
|
|
хує частинку, на ділянці (xmin , xmax ) |
||||||||
|
|
|
|
має місце притягання частинки до |
|||||||||
|
|
|
|
|
|||||||||
|
|
|
xmin |
xmax |
центру. |
|
|
|
|
|
|
||
0 |
|
|
|
Область |
(0, xmax ) називається |
||||||||
х1 |
х2 |
х3 х4 |
х5 х6 |
x |
|||||||||
|
|
|
|
|
|
|
|
||||||
Е1 |
|
|
|
|
потенціальною ямою, а ( xmin , ) – |
||||||||
|
|
|
Мал. 4.1 |
потенціальним бар’єром. Їх можна |
|||||||||
|
|
|
моделювати прямокутними |
потен- |
|||||||||
|
|
|
|
|
ціалами (мал. 4.2, а). |
|
|
|
|||||
|
Простішим |
шляхом, |
що дозволяє |
визначити |
особливості |
руху |
|||||||
мікрочастинок у складних потенціальних полях, є розглядання їх у потенціальних полях, що моделюють окремі елементи показаного на мал. 4.1
потенціалу (мал. 4.2).
Побудовані модельні поля дозволяють порівняти поведінку класичної і квантової частинок. Класична частинка з енергією Е1 (мал. 4.1) може перебувати лише в області (х3, х4), виконуючи коливання між крайніми її точками, тобто її рух буде фінітним. Частинка з енергією Е2 може здійснювати як фінітний (коливальний) рух в області (х2, х5), так і інфінітний в області (х ≥ х6). Зона ж (х5, х6) – заборонена для класичної частинки з енергією Е2. Нарешті, частинка енергією Е3 здійснює інфінітний рух в області (х > х1). Отже класична частинка не може подолати потенціальний бар’єр, якщо її енергія менша за висоту цього бар’єру.
Поведінка квантової частинки в аналогічних ситуаціях, як ми впевнимося пізніше, відрізняється від класичної. Зокрема вона може подолати бар’єр скінченної ширини (випадок Е2). Таке подолання дістало назву тунельного
40
