Примеры решения задач

Пример 1.Доказать, что следующие функции примитивно рекурсивны:а)б)в)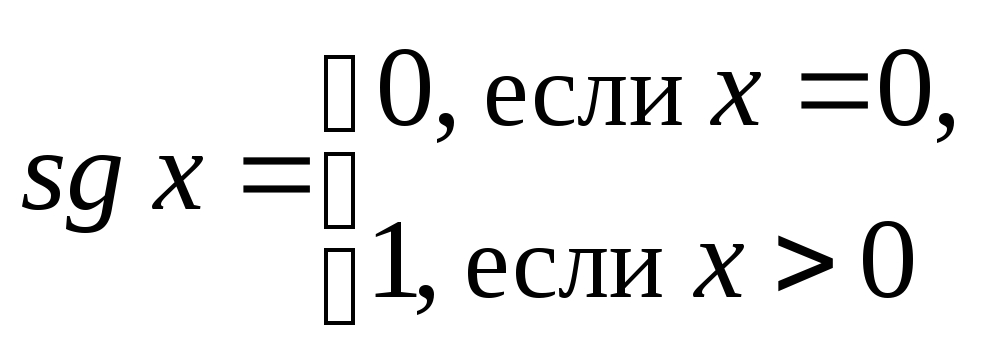(функция “сигнум”).

Решение.а)Имеем:оЭто схема примитивной рекурсии. Так как функцияпримитивно рекурсивна, то функциятоже.

б)Схема примитивной рекурсии для функциивыглядит так:s(oТак как функцияпримитивно рекурсивна, тотоже.

в)Имеем:Следовательно, функцияпримитивно рекурсивна.

Пример 2.Доказать, что функция

рекурсивна.

Доказательство.ПустьТак как функцияполучается из примитивно рекурсивных функций с помощью оператора минимизации, то функциярекурсивна. Ясно, что

Известно, что функция примитивно рекурсивна (см. предыдущее упражнение). Следовательно, функциярекурсивна. Это влечёт рекурсивность функцииа она совпадает с функцией

3.Выяснить, что из себя представляет функцияМгдефункция “сигнум” (см. предыдущую задачу).

Решение.ПустьМТогдаПоэтомуа остальные значения функциине определены.

Задачи для самостоятельного решения

1.Доказать, что следующие функции примитивно рекурсивны:

а)б)в)

в)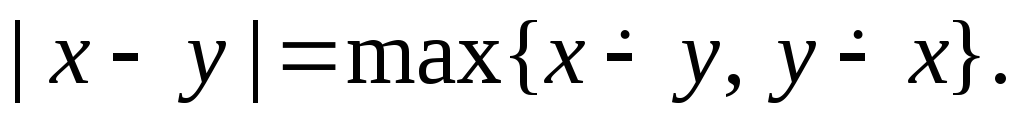

2.Доказать, что функцияявляется рекурсивной.

3.Доказать, что если функцияпримитивно рекурсивна, то функция– тоже. Используя это утверждение и результат задачи 1в), доказать примитивную рекурсивность функции

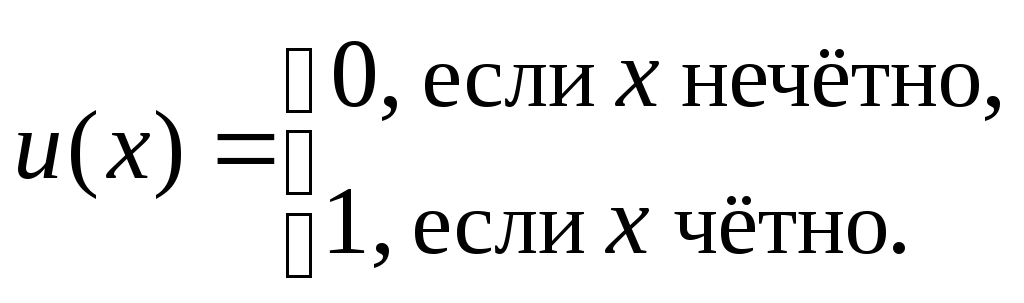
Ответы

1. Указание. а)б)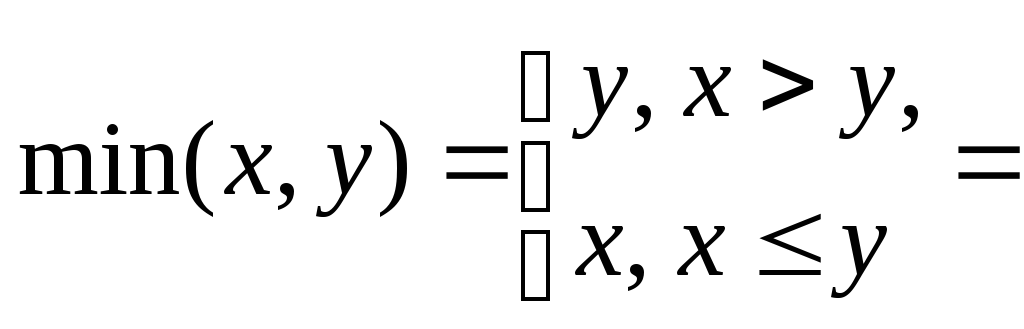

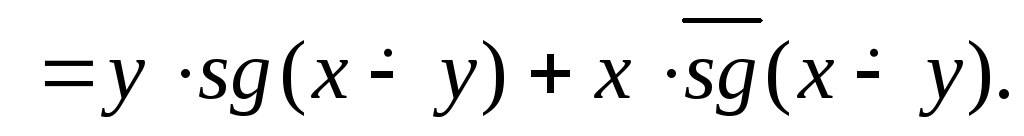2. Указание.

3. Указание:

§4.4. Алгоритмически неразрешимые задачи

В разных разделах математики встречаются алгоритмически неразрешимые задачи, т.е. задачи, для которых нет алгоритма решения, причём нет не потому что его пока не придумали, а потому что он невозможен в принципе. Разумеется, алгоритм надо понимать в смысле машин Тьюринга и рекурсивных функций (см. разделы 4.1, 4.2, 4.3). Сформулируем некоторые из этих задач. Доказывать их алгоритмическую неразрешимость мы не будем, так как это выходит далеко за рамки данного учебника.

Проблема остановки машины Тьюринга. Машина Тьюринга – это объект, определяемый конечным числом параметров. Все частичные отображения одного конечного множества в другое могут быть эффективным образом перенумерованы. Поэтому каждой машине Тьюринга можно присвоить номер (натуральное число). Пустьмашина Тьюринга с номеромНекоторые машины, начинающие работать на пустой ленте, в конце концов останавливаются, а некоторые работают бесконечно долго. Возникает задача: по натуральному числуопределить, остановится или нет машина Тьюрингазапущенная на пустой ленте. Эта задача алгоритмически неразрешима. То есть не существуетавтоматической процедуры, для каждогорешающей, останавливается или нет машинаЭто не исключает того, что для какой-либо конкретной машины мы установим, останавливается она или нет. Не существует метода, решающего этосразу для всех машин.

Проблема равенства слов. Группы и полугруппы часто задаются образующими элементами и определяющими соотношениями. Например, группаподстановок на трёхэлементном множестве имеет образующие элементыии определяющие соотношенияКаждый элемент изявляется произведением элементовивзятых, возможно, несколько раз, т.е. словом в алфавитепричём это слово в общем случае не единственно. Например,иодин и тот же элемент изВозникает вопрос: равны два данных слова в группеили нет? Существует ли алгоритм, решающий этот вопрос для любых двух слов? Для группыответ положительный: алгоритм существует, и читатель сформулирует его без труда. Однако, существуют полугруппы (и группы), для которых такого алгоритма нет. Итак, пусть полугруппазадана образующими элементамии соотношениями(слова от), то в общем случае не существует алгоритма, определяющего для двух произвольных словравны они как элементы изили не равны (т.е. следует равенствоиз равенствили не следует). Кроме того, в общем случае алгоритмически неразрешим вопрос о том, будет ли полугруппаконечной (или коммутативной, или периодической).

Проблема истинности формулы. Всякая аксиоматическая теория (например, теория групп или элементарная геометрия) определяется наличием аксиом (будем считать, что их конечное число) и правил вывода утверждений из аксиом. Утверждения, выводимые из аксиом, называются теоремами. Примеры правил вывода:

1) всякая аксиома есть теорема;

2) если итеоремы, тотеорема;

3) если итеоремы, тотеорема.

Пусть дана правильно построенная формула (т.е. не произвольный набор значков, а формула, построенная с правильным употреблением логических связок, расстановки скобок и т.д.). Является литеоремой, т.е. выводима лииз аксиомСуществуют аксиоматические теории, для которых выяснить для произвольной формулыистинна ли она (т.е. является ли теоремой), алгоритмически неразрешимо.

209