Решение типовых задач

Пример 1.Построить машину Тьюринга, вычисляющую функцию:

а) б)

Решение. а) Фактически надо, имея следующую ситуацию на ленте

уничтожить все единицы, кроме первой. Пусть состояние, в котором машина ищет крайнюю правую единицу, попутно стирая все единицы, начиная со второй,движение влево до оставшейся единицы. Программа машины выглядит так:

б) Словесно алгоритм вычисления функции можно сформулировать так: будем заменять в массивах из единиц последние единицы нулями до тех пор, пока в одном или обоих массивах не останется ровно одна единица; затем заменим все нули, стоящие между массивами из единиц, единицами; наконец, удалим две последние единицы.

Программа машины выглядит так:

	находим последнюю единицу в первом массиве из единиц и стираем её, если она не единственная
	то же делаем со вторым массивом из единиц
	возвращаемся к крайней левой единице
	заменяем промежуточные нули единицами
	стираем последние две единицы и останавливаемся у крайней левой единицы

2. Определить, какую функцию вычисляет машина Тьюринга, заданная следующей программой:

Решение.Если внимательно проследить за работой машины, то можно заметить, что если вначале на ленте была только одна единица, то машина, перейдя в состояниееё сотрёт и затем будет работать бесконечно долго, а если на ленте более одной единицы, то она сотрёт последнюю из них и остановится около первой. Поэтому

Задачи для самостоятельного решения

1.Построить машину Тьюринга, реализующую функцию:

а) б)

2.Определить, какие функции вычисляют следующие машины Тьюринга:

а)

		(функция двух переменных)

б)

		(функция одного переменного)

Ответы

1. а)

		(ответ неоднозначен)

1. б)

		(ответ неоднозначен)

2. а)б)

§4.3. Рекурсивные функции

Напомним, что в этой главе множество натуральных чисел содержит 0, т.е.Будем рассматривать функции (возможно, частичные)Таким образом, если, то либо, либоне определено. Введём в рассмотрениепростейшие функции

о s I

Эти функции могут быть вычислены с помощью соответствующего механического устройства (например, на машине Тьюринга). Определим операторы, которые по одной или нескольким заданным функциям строят новые функции.

Оператор суперпозиции. Пусть даны функцияотпеременных ифункцийотпеременных.. Суперпозицией функцийназывается функция

Мы говорим, что функция получается применением оператора суперпозицииSк функциями пишемS

Например, S(s,o) – это функцияs(oт.е. функция, тождественно равная 1, аS(s,s) – это функция

Оператор примитивной рекурсии. Пусть даны функциииПостроим функциюПусть зафиксированы значенияТогда полагаем:

Эти равенства определяют функцию однозначно. Функцияназывается функцией, полученной с помощью оператораRпримитивной рекурсии. Используется записьR

Индуктивное определение функции (продемонстрированное в операторе примитивной рекурсии) в математике не редкость. Например, индуктивно определяются степень с натуральным показателем: факториал:и т.д.

Определение. Функции, которые могут быть получены из простейшихоsIприменением конечного числа раз операторов суперпозиции и примитивной рекурсии, называютсяпримитивно рекурсивными.

Проверим, что функция является примитивно рекурсивной. Действительно, мы имеем:Это есть схема примитивной рекурсии, так какIаsSs,ЗдесьIаsS(s,I

Аналогично доказывается, что функции (считаем по определениюи многие другие являются примитивно рекурсивными.

Отметим, что примитивно рекурсивные функции всюду определены(т.е. определены для всех значений их аргументов). Действительно, простейшие функцииo,s,Iявляются всюду определёнными, а применение операторов суперпозиции и примитивной рекурсии ко всюду определённым функциям даёт также всюду определённые функции. Значит, такая функция, как

примитивно рекурсивной быть не может. Рассматривать функцию здесь мы не имеем права, так как значения функций должны быть натуральными числами. Однако, можно рассмотреть функцию

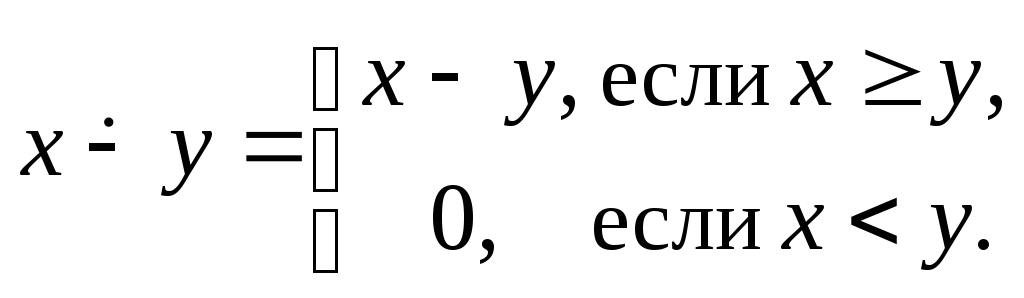
Проверим, что она примитивно рекурсивна. Докажем вначале, что функция примитивно рекурсивна. Действительно,что служит схемой примитивной рекурсии для функцииНаконец,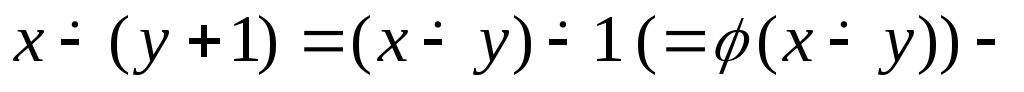схема примитивной рекурсии для

Существенно более широким классом функций, чем примитивно рекурсивные функции, является класс рекурсивныхфункций (определение см. ниже). В литературе эти функции называют такжечастично рекурсивными. Для их определения введём ещё один оператор.

Оператор минимизации. Пусть дана функцияЗафиксируем какие-либо значенияпервыхпеременных и будем вычислятьи т.д. Еслинаименьшее натуральное число, для которого(т.е. значениявсе существуют и не равныто полагаемТаким образом,

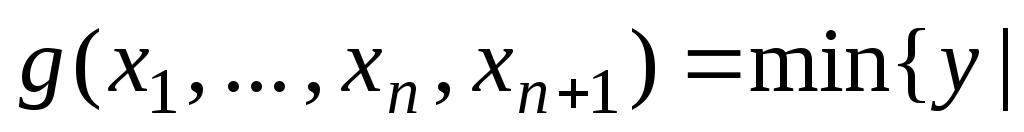
Если такого нет, то считаем, чтоне определено. Итак, возможны три случая:

1. существуют и не равныа

2. существуют и не равныане существует;

3. существуют при всехи отличны от

Если имеет место 1-й случай, то а если 2-й или 3-й, тоне определено. Про функциюполученную таким образом, говорят, что она получена изприменением оператора минимизацииМ. Мы пишемМ

Оператор минимизации – это очевидное обобщение оператора взятия обратной функции. Обобщение довольно глубокое, так как от функции не требуется, чтобы она была взаимно однозначной (по переменной

Функции, которые могут быть получены из простейших оsIприменением конечного числа раз операторов суперпозиции, примитивной рекурсии и минимизации, называются рекурсивными.

Класс рекурсивных функций шире класса примитивно рекурсивных функций хотя бы по тому, что он содержит не только всюду определённые функции. Докажем, например, что функция

является рекурсивной. Действительно, а ранее было установлено, что функцияпримитивно рекурсивна.

Рекурсивные функции отражают наше интуитивное представление о функциях, вычислимых некоторым механическим устройством. В частности, они вычислимы на машинах Тьюринга (см. предыдущий раздел). Наоборот, всякая функция, вычислимая на машине Тьюринга, рекурсивна. Мы не будем проверять этот факт, так как это потребовало бы слишком много времени и места. Полное доказательство можно найти, например, в книге А.И.Мальцева “Алгоритмы и рекурсивные функции”. В предыдущем разделе, впрочем, были построены машины Тьюринга, реализующие функции osIС другой стороны, не всякая функция натуральных аргументов является рекурсивной, даже не всякая функция одного аргумента. В самом деле, рекурсивных функций имеется лишь счётное число (т.е. их можно занумеровать натуральными числами), а все функцииобразуют несчётное множество. Существование нерекурсивных функций и является “математической причиной” наличия алгоритмически неразрешимых задач (о них см. следующий раздел).