Свойства операций над высказываниями

1. а) (коммутативность дизъюнкции);

б) (коммутативность конъюнкции);

2. а) (ассоциативность дизъюнкции);

б) (ассоциативность конъюнкции);

3. а) (дистрибутивность дизъюнкции относительно конъюнкции);

б) (дистрибутивность конъюнкции относительно дизъюнкции);

4. и–законы де Моргана.

5. ;;;

6. (или) (закон исключенного третьего);

(или (закон противоречия);

7. (или);(или);

(или );(или).

Приведенные свойства обычно используются для преобразования и упрощения логических формул. Здесь приведены свойства только трех логических операций (дизъюнкции, конъюнкции и отрицания), но дальше будет показано, что все другие операции могут быть выражены через них.

С помощью логических связок можно составлять логические уравнения, и решать логические задачи подобно тому, как решаются арифметические задачи с помощью систем обычных уравнений.

Пример.Однажды следователю пришлось одновременно допрашивать трех свидетелей: Клода, Жака и Дика. Их показания противоречили друг другу, и каждый из них обвинял кого-нибудь во лжи. Клод утверждал, что Жак лжет, Жак обвинял во лжи Дика, а Дик уговаривал следователя не верить ни Клоду, ни Жаку. Но следователь быстро вывел их на чистую воду, не задав им ни одного вопроса. Кто из свидетелей говорил правду?

Решение. Рассмотрим высказывания:{Клод говорит правду};{Жак говорит правду};{Дик говорит правду}.

Нам не известно, какие из них верны, но известно следующее:

1) либо Клод сказал правду, и тогда Жак солгал, либо Клод солгал, и тогда Жак сказал правду;

2) либо Жак сказал правду, и тогда Дик солгал, либо Жак солгал, и тогда Дик сказал правду;

3) либо Дик сказал правду, и тогда Клод и Жак солгали, либо Дик солгал, и тогда неверно, что оба других свидетеля солгали (т.е. хотя бы один из этих свидетелей сказал правду).

Выразим эти высказывания в виде системы уравнений:

Условие задачи будет выполнено, если одновременно истинны эти три высказывания, а значит истинна их конъюнкция. Перемножим эти равенства (т.е. возьмем их коньюнкцию)

.

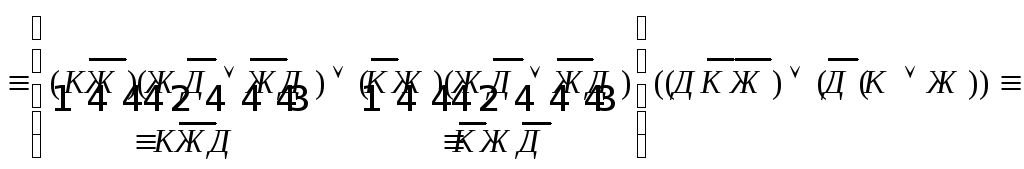
Но в том и только том случае, если, а. Следовательно, Жак говорит правду, а Клод и Дик лгут.

Любая -членная операция, обозначаемая, например,, будет полностью определена, если установлено, при каких значениях высказыванийрезультат будет истинным или ложным. Один из способов задания такой операции – заполнение таблицы значений:

И	И		И	И или Л
Л	Л		Л	И или Л

В таблице значений высказывания, образованного от простейших высказываний, имеетсястрок. Столбец значений имеет такжепозиций. Следовательно, имеетсяразличных вариантов его заполнения, и, соответственно, число всех-членных операций равно. Причисло одночленных операций равно 4, причисло двучленных – 16, приколичество трехчленных – 256 и т.д.

Рассмотрим некоторые специальные виды формул.

Формулу называют элементарной конъюнкцией, если она является конъюнкцией переменных и отрицаний переменных. Например, формулы,,,– элементарные конъюнкции.

Формулу, представляющую собой дизъюнкцию (возможно одночленную) элементарных конъюнкций, называют дизъюнктивной нормальной формой(д. н. ф.). Например, формулы,,.

Теорема 1 (о приведении к д. н. ф. ). Для любой формулыможно найти равносильную ей формулу, являющуюся д. н. ф. .

Эта теорема и следующая за ней теорема 2 будут доказаны в следующем пункте. Применяя эти теоремы, можно стандартизировать вид логических формул.

Формулу называют элементарной дизъюнкцией, если она является дизъюнкцией переменных и отрицаний переменных. Например, формулы,,и т.д.

Формулу, являющуюся конъюнкцией (возможно одночленной) элементарных дизъюнкций, называют конъюнктивной нормальной формой(к. н. ф.). Например, формулы,.

Теорема 2 (о приведении к к. н. ф.). Для любой формулыможно найти равносильную ей формулу, являющуюся к. н. ф.