
Полином Жегалкина
Полиномом
Жегалкина(полиномом по модулю 2)
от переменных![]() называется выражение вида
называется выражение вида
![]()
где
![]() .
.
Наибольший
из рангов элементарных конъюнкций
входящих в полином, называется степенью
этого полинома. Степень полинома
0 принимается равной![]() .
Число слагаемых в формуле полинома
называетсядлиной полинома.
.
Число слагаемых в формуле полинома
называетсядлиной полинома.
Теорема.Каждая функция из![]() представляется в виде полинома Жегалкина
и это представление единственно.
представляется в виде полинома Жегалкина
и это представление единственно.
Доказательство.Существование полинома для каждой булевой функции, отличной от константы 0, следует из того, что ее СДНФ применением равенств
![]()
сводится к полиному.
Для
доказательства единственности подсчитаем
число полиномов Жегалкина от переменных
![]() ,
т.е. число выражений вида
,
т.е. число выражений вида
![]() .
.
Число
слагаемых
![]() в указанной сумме равно количеству
подмножеств
в указанной сумме равно количеству
подмножеств![]() из
из![]() чисел
чисел![]() ,
т.е.
,
т.е.![]() .
Каждому полиному в соответствие можно
поставить вектор
.
Каждому полиному в соответствие можно
поставить вектор![]() длины
длины![]() ,
компонентами которого являются числа
,
компонентами которого являются числа![]() ,
равные 0 или 1. Следовательно, искомое
число полиномов равно
,
равные 0 или 1. Следовательно, искомое
число полиномов равно![]() ,
т.е. числу всех булевых функций от
переменных
,
т.е. числу всех булевых функций от
переменных![]() .
.
Следствие.Из доказанной теоремы вытекает единственность представления булевой функции посредством полинома Жегалкина.
Приведем основные методы построения полиномов Жегалкина от заданной функции.
1. Метод
неопределенных коэффициентов.
Пусть![]() – искомый полином Жегалкина, реализующий
заданную функцию
– искомый полином Жегалкина, реализующий
заданную функцию![]() .
.
Запишем его в виде
![]()
Вектор
![]() длины
длины![]() назовемвектором коэффициентов
полинома
назовемвектором коэффициентов
полинома ![]() .
Найдем его компоненты. Для этого заметим,
что если переменным
.
Найдем его компоненты. Для этого заметим,
что если переменным![]() придать значения
придать значения![]() из
из![]() -ой
строки таблицы, то значение
-ой
строки таблицы, то значение![]() будет равно сумме
будет равно сумме![]() с компонентами вектора
с компонентами вектора![]() ,
соответствующими ненулевым конъюнкциям
,
соответствующими ненулевым конъюнкциям![]() (
(![]() ).
В итоге получим систему из
).
В итоге получим систему из![]() уравнений с
уравнений с![]() неизвестными, имеющую единственное
решение. Решив ее, находим коэффициенты
полинома
неизвестными, имеющую единственное
решение. Решив ее, находим коэффициенты
полинома![]() .
.
2.
Метод, основанный на преобразовании
формул над множеством связок
![]() .Строят некоторую формулу
.Строят некоторую формулу![]() над множеством связок
над множеством связок![]() ,
реализующую данную функцию
,
реализующую данную функцию![]() .
Затем заменяют всюду подформулы вида
.
Затем заменяют всюду подформулы вида![]() на
на![]() ,
раскрывают скобки, пользуясь дистрибутивным
законом
,
раскрывают скобки, пользуясь дистрибутивным
законом![]() ,
и применяют эквивалентности
,
и применяют эквивалентности![]() .
.
Пример.Построить полином Жегалкина функции![]() .
.
Решение.1. (Метод неопределенных коэффициентов).
Запишем искомый полином в виде![]()
Табл. 1.11
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
![]()
![]()
![]()
![]()
Получаем систему уравнений

Из
системы уравнений находим
![]() .
.
Следовательно,
![]()
2. (Метод преобразования формул). Имеем
![]()
Задачи для самостоятельного решения
1. Представить в виде СДНФ следующие функции:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ;
;
г)
![]() .
.
2. Представить в виде СКНФ следующие функции:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ;
;
г)
![]() .
.
3.
Подсчитать число функций
![]() ,
у которых СДНФ удовлетворяет следующему
условию:
,
у которых СДНФ удовлетворяет следующему
условию:
а) содержит не более двух элементарных конъюнкций;
б) отсутствуют элементарные конъюнкции, у которых число букв с отрицаниями равно числу букв без отрицаний;
в)
каждая элементарная конъюнкция содержит
хотя бы две буквы с отрицаниями (![]() );
);
г) отсутствуют элементарные конъюнкции, содержащие нечетное число букв с отрицаниями;
д) в каждой элементарной конъюнкции число букв с отрицаниями не больше числа букв без отрицаний.
4.
Подсчитать число функций
![]() ,
у которых СКНФ является одновременно
и ДНФ (необязательно совершенной).
,
у которых СКНФ является одновременно
и ДНФ (необязательно совершенной).
5.
Найти длину СДНФ функции
![]() :
:
а)
![]()
б)
![]()
6.
С помощью эквивалентных преобразований
построить какую-нибудь ДНФ функции
![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
7.
С помощью эквивалентных преобразований
построить какую-нибудь КНФ функции
![]() :
:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
8.
Применяя преобразования вида
![]() и
и![]() ,
построить из заданной ДНФ функции
,
построить из заданной ДНФ функции![]() ее СДНФ:
ее СДНФ:
а)
![]() ;
;
б)
![]() .
.
9.
Применяя преобразования вида
![]() и
и![]() ,
построить из заданной КНФ функции
,
построить из заданной КНФ функции![]() ее СКНФ:
ее СКНФ:
а)
![]() ;
;
б)
![]() .
.
10. Методом неопределенных коэффициентов найти полиномы Жегалкина для следующих функций:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]()
11.
Используя метод, основанный на
преобразовании формул над множеством
связок
![]() ,
найти полиномы Жегалкина для следующих
функций:
,
найти полиномы Жегалкина для следующих
функций:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ;
;
г)
![]() .
.
12. Найти число:
а)
полиномов Жегалкина степени
![]() над множеством переменных
над множеством переменных![]()
![]()
б)
полиномов Жегалкина степени
![]() над множеством
над множеством![]() ,
обращающихся в 1 на наборе
,
обращающихся в 1 на наборе![]()
![]()
в)
полиномов Жегалкина длины
![]() над множеством
над множеством![]() ,
,![]()
г)
полиномов Жегалкина длины
![]() над множеством
над множеством![]() ,
удовлетворяющих условию: в полиноме не
могут содержаться одновременно (в
качестве слагаемых) конъюнкции одинакового
ранга
,
удовлетворяющих условию: в полиноме не
могут содержаться одновременно (в
качестве слагаемых) конъюнкции одинакового
ранга![]()
13.
Выяснить, на скольких наборах из
![]() обращается в единицу полином
обращается в единицу полином![]() :
:
а)
 ;
;
б)
 .
.
14.
Найти функцию
![]() ,
у которой длина полинома Жегалкина в
,
у которой длина полинома Жегалкина в![]() раз превосходит длину ее СДНФ (
раз превосходит длину ее СДНФ (![]() ).
).
Ответы
1.
а)![]() ;б)
;б)![]()
![]() ;в)
;в)![]() ;
;
г)![]() .
.
2.
а)![]() ;б)
;б)![]()
![]() ;в)
;в)![]()
![]() г)
г)![]()
![]() .
.
3.
а)![]() ;
б) если
;
б) если![]() четное, то
четное, то![]() ;
если
;
если![]() нечетное, то
нечетное, то![]() ;в)
;в)![]() ;г)
;г)![]() ;д)если
;д)если![]() нечетное, то
нечетное, то![]() ,
если
,
если![]() четное, то
четное, то![]() .4.
.4.![]() .
.
5.
а)![]() ;б)
;б)![]() .6. а)
.6. а)![]() ;
;
б)![]() ;в)
;в)![]() ;г)
;г)![]() .
.
7.
а)![]() ;б)
;б)![]() .
.
8.
а)![]() ;
;
б)![]() ;в)
;в)![]() .
.
9.
а)![]()
![]() .10. а)
.10. а)![]() ;
;
б)![]() ;в)
;в)![]() ;
;
г)![]() .
.
11.
б)![]() ;
;
в)![]() .
.
12.
а)1 при![]() ;
;![]() ,
где
,
где![]() при
при![]() ;б)
;б)![]() ;в)
;в)![]() ;г)
;г)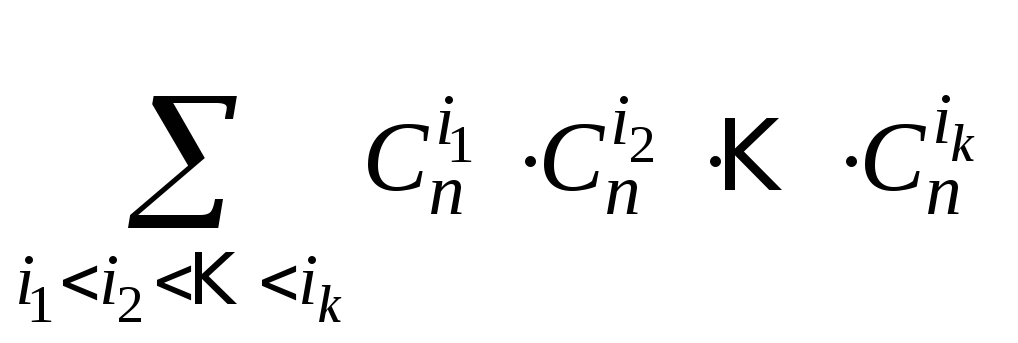 .
.
13.
а)![]() ;б)
;б)
![]() .
14.
.
14.![]() .
.
