3.8. Матрицы, ассоциированные с графом
Во многих задачах теории графов (особенно
реализуемых на ЭВМ) графы удобно описывать
матрицами. Пусть
 - произвольный неориентированный граф
с m вершинами и n
ребрами. Занумеруем вершины графа .
- произвольный неориентированный граф
с m вершинами и n
ребрами. Занумеруем вершины графа .
Определение. Матрицей
смежности неориентированного
графа
 называется матрица
называется матрица
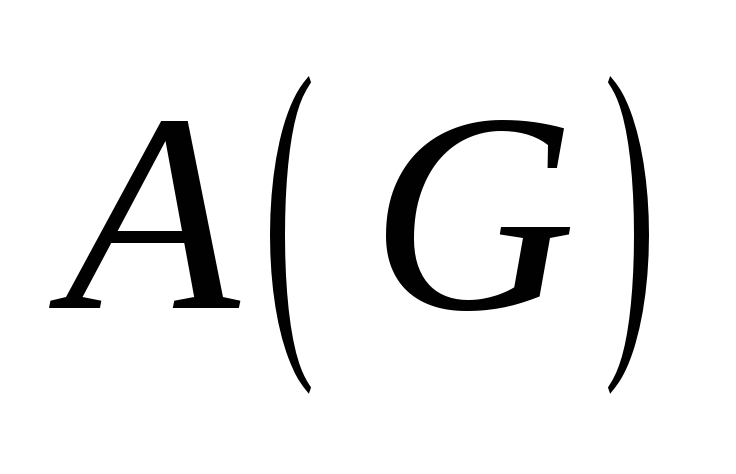 размера
размера
 ,
элементы которой
,
элементы которой
 ,
где
,
где
 - число ребер, соединяющих вершины
с номерами
- число ребер, соединяющих вершины
с номерами
 ,
причем при
,
причем при
 каждую петлю учитываем дважды.
каждую петлю учитываем дважды.
Замечание.
Для каждого графа имеется несколько
матриц смежности, отвечающих различным
упорядочениям множества вершин графа.
Очевидно, что одна такая матрица смежности
получается из другой с помощью некоторой
перестановки строк и аналогичной
перестановки столбцов.
Помимо вершин занумеруем ребра графа.
Определение. Матрицей
инцидентности неориентированного
графа
 называется матрица
называется матрица
 размера
размера
 ,
элементы которой
,
элементы которой
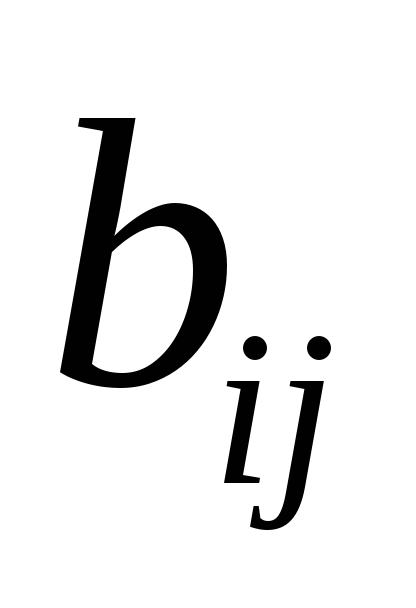 определены следующим:
определены следующим:
1.
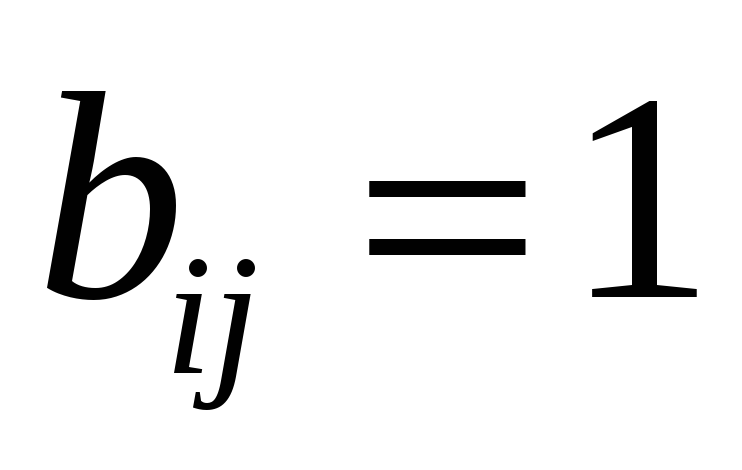 ,
если вершина с номером i
инцидентна ребру с номером j
и j-ое ребро не
является петлей;
,
если вершина с номером i
инцидентна ребру с номером j
и j-ое ребро не
является петлей;
2.
 во всех остальных случаях.
во всех остальных случаях.
Замечание.
Для каждого графа имеется несколько
матриц инцидентности, отвечающих
различным упорядочениям множества
вершин и ребер графа. Очевидно, что одна
такая матрица инцидентности получается
из другой с помощью некоторой перестановки
строк и некоторой перестановки столбцов.
П ример.
ример.
 ;
;
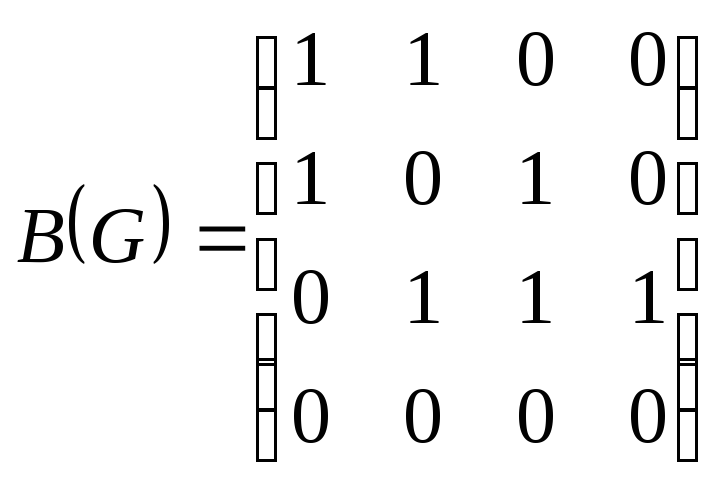 .
.
44


 ример.
ример.
 ;
;
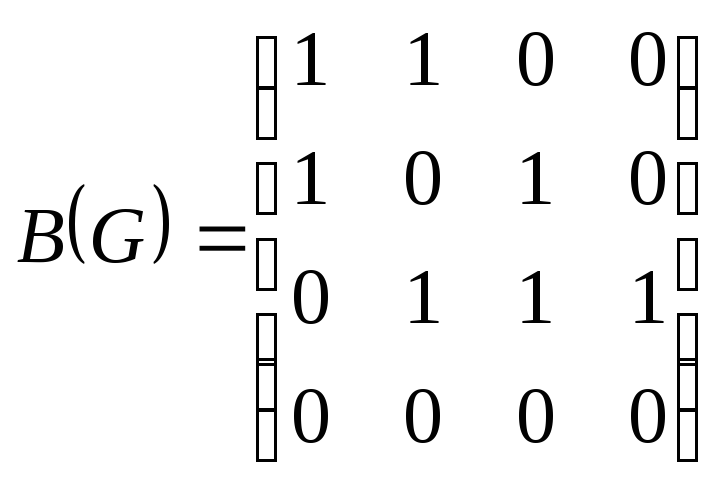 .
.