
Курс лекций по высшей математике. 2 часть
.pdf
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
3 |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
dx |
1 |
|
|
|
|
dx |
|
|
65 |
|
26 |
dx |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x2 |
4x 3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
20 x 1 52 x 3 |
|
|
x2 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
4x 5 |
|
|
|
4x 5 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
ln |
|
x 3 |
|
|
|
1 |
|
|
|
|
|
|
|
4x 15 |
. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
ln |
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
20 |
|
52 |
130 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Вычислим |
последний |
|
интеграл, |
введя |
новую |
переменную: |
|||||||||||||||||||||||||||||||||||||||||||||
x 2 |
z, |
x z |
2, |
|
dx |
|
|
dz; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4x 15 |
|
dx |
|
|
|
4z 7 |
dz 2 |
|
|
d z 2 |
1 |
|
7 |
|
|
|
|
|
dz |
|
|
|
2ln z 2 1 |
||||||||||||||||||||||||||||
|
x 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1 |
|
|
|
|
z 2 |
1 |
|
|
|
|
|
|
|
|
|
z 2 |
1 |
|
|
|
|
|
|
|
|
z 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
7 arctg z |
C |
2 ln |
|
x2 |
|
|
4x |
5 |
|
|
|
|
7 arctg x |
2 |
|
|
|
C. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
x |
1 |
|
|
ln |
x 3 |
|
|||||||||||||||||
Следовательно, |
|
x2 |
4x 3 x2 |
|
|
|
4x 5 |
20 |
52 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
ln x2 4x |
5 |
|
7 |
|
arctg x |
2 |
C. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
65 |
130 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
§4. Интегрирование тригонометрических функций |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
1.Интегралы |
|
|
вида |
|
|
|
|
|
|
|
sin kx sin mxdx, |
|
|
|
|
|
sin kx cos mxdx, |
||||||||||||||||||||||||||||||||||
cos kx cos mxdx вычисляются преобразованием произведения триго-
cos mxdx вычисляются преобразованием произведения триго-
нометрических функций в сумму по формулам:
|
sin kx sin mx |
|
|
1 |
|
|
cos k |
m x |
cos k |
m x |
, |
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
sin kx cos mx |
|
|
|
1 |
|
|
sin k |
m x |
sin k |
m x |
, |
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
cos kx cos mx |
|
|
|
1 |
|
|
cos k |
m x |
cos k |
|
m x . |
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
sin 3x |
cos 5xdx |
1 |
|
|
|
|
|
sin |
|
2x sin 8x dx |
|
1 |
|
sin 2xdx |
1 |
|
sin 8xdx |
||||||||||||
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
1 |
sin 2xd 2x |
|
|
|
|
|
1 |
|
1 |
|
sin8xd 8x |
1 |
cos 2x |
|
1 |
cos 8x |
C. |
|||||||||
2 |
2 |
|
|
|
|
2 |
|
8 |
|
4 |
16 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
23

2.Интегралы вида cos m x  sinn xdx , где m или n– нечетное положи-
sinn xdx , где m или n– нечетное положи-
тельное число, вычисляются подведением под знак дифференциала. Например,
|
cos3 x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
dx |
sin 2 x |
cos 2 x |
cos xdx |
cos xdx |
d sin x; cos 2 x 1 sin2 x |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
sin |
|
|
2 x 1 |
d sin x |
|
sin 2 |
xd sin x |
sin 2 xd sin x |
||||||||||||||
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 sin 2 x |
sin 2 |
|
|
|
|
|
|
sin5 x C. |
|
|
|
|||||||||||||
x C |
2 |
|
sin x |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|||
3.Интегралы вида cos m x  sinn xdx , где m и n–четные положи-
sinn xdx , где m и n–четные положи-
тельные числа, вычисляются с помощью формул понижения степени:
|
|
sin |
2 |
|
|
1 |
1 |
|
cos 2 |
|
|
|
|
|
; cos 2 |
|
1 |
|
1 |
cos 2 |
; sin |
|
cos |
|
1 |
sin 2 . |
||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
sin2 3x cos 2 3xdx |
|
|
|
sin 6x |
|
dx |
|
sin2 6xdx |
|
1 |
cos12x dx |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
4 |
|
4 |
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
dx |
1 |
|
cos12dx |
|
1 |
x |
1 |
|
|
|
1 |
|
sin12x |
|
C |
|
x |
|
sin12x |
|
C. |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
8 |
|
8 |
|
|
|
|
|
|
|
8 |
|
|
8 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
96 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
4.Интегралы |
|
|
tg m xdx, сtg m xdx, где m N, вычисляются заменой |
|||||||||||||||||||||||||||||||||||||||||||||||||||
переменной: tg x |
|
z, x |
|
|
|
|
arctg z, dx |
|
|
|
|
|
|
dz |
|
|
или сtg x |
z, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
z |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x |
arcctg z, dx |
|
|
|
|
dz |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
tg 3 xdx |
|
|
z3dz |
|
|
|
|
|
неправильн ая дробь |
z3 |
z |
z |
dz |
|
|
z z 2 |
1 |
dz |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
z 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
zdz |
|
|
|
|
|
zdz |
|
1 |
|
d 1 |
z 2 |
|
z 2 |
|
|
|
1 |
ln 1 |
|
z 2 |
C |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
z 2 |
|
|
|
|
|
2 |
|
1 |
|
|
z 2 |
2 |
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
tg 2 x |
|
|
1 |
ln 1 |
tg 2 x |
|
|
C. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
24

5.Интегралы вида R sin x,cos x dx сводятся к интегралам от ра-
циональных дробей с помощью универсальной тригонометрической
подстановки tg 2x
|
|
cos x |
|
|
1 |
z2 |
|
||||
|
|
|
1 |
z2 |
|
||||||
|
|
|
|
|
|
|
|||||
ля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 tg |
x |
|
|||
|
|
|
x |
|
|
|
|
|
|
||
cos |
2 |
|
]= |
|
2 |
|
|
||||
|
2 |
1 |
|
tg 2 |
x |
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
||
Например,
z , тогда x |
|
2arctg z, dx |
|
|
|
|
2dz |
|
, sin x |
2z |
, |
|||||||||||||
|
|
|
|
1 z 2 |
|
1 z2 |
||||||||||||||||||
|
|
|
2 sin |
|
x |
cos |
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(т.к. sin x |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
=[после деления числите- |
||||||||||
cos 2 |
|
x |
|
sin2 |
|
x |
|
|||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
знаменателя |
|
|
|
на |
||||||||||
|
cos 2 |
|
x |
|
sin2 |
|
x |
|
|
1 |
|
|
tg 2 |
x |
|
|
|
|
||||||
; cos x |
2 |
|
2 |
|
|
|
|
|
2 |
|
). |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cos 2 |
|
|
sin2 |
|
|
|
|
1 |
|
|
tg 2 |
|
|
|
|
|||||||||
|
|
x |
|
|
x |
|
|
|
|
x |
|
|
|
|
||||||||||
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2dz
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
1 |
|
z |
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
dz |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8 |
|
4 sin x 7 cos x |
|
8 |
4 |
|
2z |
|
7 |
1 |
z 2 |
8 |
|
8z 2 8z |
7 |
7z 2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z 2 |
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
dz |
|
|
|
|
|
|
|
d z 4 |
|
|
|
1 |
|
z 4 |
1 |
|
|
tg |
x |
|
|
5 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
ln |
|
|
|
|
|
|
|
C ln |
|
|
|
|
|
C. |
|||||
|
z2 8 z 15 |
|
|
|
z 4 2 |
1 |
|
|
2 |
z 4 1 |
|
tg |
x |
3 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
Следует заметить, что использование универсальной подстановки |
||||||||||||||||||||||||||||||||||||||
нередко приводит к громоздким выкладкам. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
§5. Интегрирование простейших иррациональностей |
||||||||||||||||||||||||||||||||||||||
|
|
Рассмотрим методы интегрирования простейших видов иррацио- |
||||||||||||||||||||||||||||||||||||||
нальностей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1. |
|
ax |
b dx |
|
|
|
.Функции такого вида интегрируются так же, как |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
mx2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
nx |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
простейшие рациональные дроби 3–го типа: в знаменателе из квадратного трехчлена выделяется полный квадрат и вводится новая переменная.
25
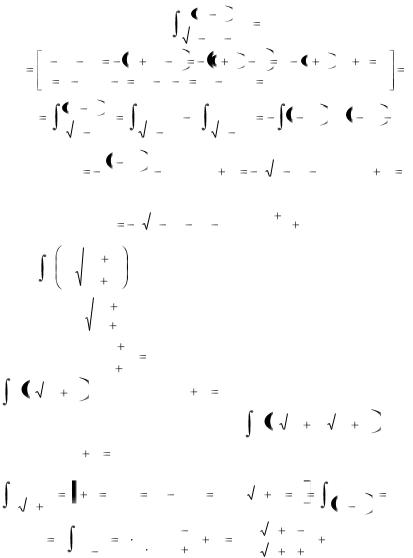
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
1 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2x |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 2x x2 |
|
|
|
|
|
x2 |
|
2x 3 |
|
|
|
x 1 2 |
|
|
|
4 4 x 1 2 ; x 1 z, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x z 1, 2x 1 2z 2 1 2z 3, dx dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2z |
3 dz |
|
|
|
|
|
|
|
|
2zdz |
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
4 |
|
z2 |
|
|
2 d 4 |
|
z2 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
z2 |
|
|
|
|
|
|
|
4 |
z2 |
4 |
|
z2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
4 |
|
z |
2 |
2 |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
||||||||||||
|
|
3 arcsin |
|
|
|
|
|
|
3 arcsin |
|
|
C |
2 |
4 |
|
|
z2 |
|
|
3 arcsin |
|
|
C |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 arcsin |
x |
1 |
|
C. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
2x |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2. |
|
R |
x, n |
ax |
|
|
b |
|
|
|
dx (под знаком интеграла–рациональная функция |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
cx |
|
|
d |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
аргументов |
|
x, |
n |
ax |
b |
|
). Интегралы такого вида вычисляются с помо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
cx |
d |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
щью |
замены |
|
|
|
ax |
|
b |
|
|
z n . |
|
|
В |
|
частности, |
в |
интегралах |
вида |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
cx |
|
d |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z n . Если подынтегральная функ- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
R x, n ax |
b dx обозначают ax |
|
b |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
ция содержит корни разных степеней: |
|
R x, m ax |
b, k ax |
b dx , то |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
обозначают ax |
b |
|
|
|
z n , где n– наименьшее общее кратное чисел m,k. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2 , x |
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2zdz |
|
|||||||||||||||
|
|
|
|
|
|
|
x |
9 |
|
|
|
|
|
9, dx |
|
|
2zdz, |
|
|
x |
9 |
|
|
|
z |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2 |
9 z |
|
|||||||||||||||||||||||||||||||||||||||||
|
x x |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
dz |
|
|
|
|
2 |
|
|
|
|
1 |
|
|
ln |
z 3 |
|
|
C |
|
1 |
ln |
|
x 9 3 |
|
|
C. |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
9 |
|
|
|
|
|
|
|
|
2 3 |
z 3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
x 9 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
6 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
dx |
|
|
x |
z |
6 ,dx |
|
|
6z5dz,6 x |
z,3 x |
z 2 , x |
z3 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
1 |
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 z 6z5dz |
6 |
|
|
z3 |
z 2 dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
z |
2 |
|
|
z |
3 |
|
|
|
|
|
|
|
|
z 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
–неправильная рациональная дробь, выделим целую часть: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
z 3 |
z 2 |
|
|
|
|
|
|
|
|
|
|
z 2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z 3 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
z |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
z 2 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– z |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6 |
z |
|
1 |
|
|
|
z |
1 |
dz |
6 zdz |
6 |
dz |
6 |
|
zdz |
|
|
|
6 |
|
|
dz |
|
|
|
6 |
|
z |
2 |
6 z |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
z 2 |
1 |
|
z |
2 |
|
|
1 |
|
z 2 |
1 |
|
2 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6 |
ln z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1 |
|
|
6 arctg z |
C |
33 |
|
x |
66 |
x |
|
3 ln 3 |
|
x |
1 |
6 arctg 6 x |
|
C. |
|
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
3.Интегралы |
|
|
вида |
|
R x, |
|
|
a2 |
|
|
x2 dx, |
|
|
|
|
|
|
|
|
R x, |
a2 |
x2 |
dx, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
R x, |
x2 |
|
|
a2 |
dx |
вычисляются с помощью тригонометрических под- |
|||||||||||||||||||||||||||||||||||||||||||||||||
становок:
1 |
R |
x, |
a 2 |
x2 |
|
|
|
dx; x |
|
a sin z; dx |
|
a сos zdz; |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a2 |
x2 |
|
|
|
a2 |
|
|
|
a2 sin2 z |
|
a |
1 sin2 z |
|
a cos z. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
adz |
; |
|
|
|
|||||||
2 |
R |
x, |
|
|
a2 |
x2 |
dx; |
x |
|
a tg z; dx |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2 z |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
||
|
a2 |
x2 |
|
|
|
a2 |
|
|
|
a2 tg 2 z a 1 tg |
2 z |
|
|
. |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
cos z |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a sin zdz |
; |
|
|
|||||||||||||||
3 |
R |
x, |
|
|
x2 |
a2 |
dx; x |
|
; dx |
|
|
|||||||||||||||||||||||
|
|
cos z |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2 |
z |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
1 |
cos 2 z |
|
a sin z |
|
|
||||||||||||||
|
x2 |
a2 |
|
|
|
|
a2 |
|
a |
a tg z. |
||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
cos z |
||||||||||||||||
|
|
|
|
|
|
cos |
z |
|
|
|
|
|
|
|
cos |
z |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
27

|
Пример 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||
|
|
|
|
|
|
dx |
|
|
|
x |
|
|
tg z,dx |
|
|
|
, 1 |
|
x2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 2 z |
|
|
|
cos z |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos 4 zdz |
|
|
|
|
|
|
cos zdz |
|
|
|
|
sin |
|
4 zd sin z |
||||||||||||||||||||
|
cos z |
|
|
tg 4 z |
cos 2 z |
|
|
sin4 z cos3 z |
|
|
|
|
|
sin4 |
z |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
sin |
3 z |
|
|
|
|
C |
1 |
|
|
|
C |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
C |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 sin3 z |
|
|
|
|
|
|
|
tg 3 x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
cos3 x |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
x2 3 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
x3 |
|
|
|
|
|
3x3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
x2 |
4 |
x2 dx |
|
|
|
|
x |
2 sin z,dx |
2 cos zdz, |
4 |
|
|
x2 |
|
|
2 cos z |
|
|
|
4 sin2 z 2 cos z |
||||||||||||||||||||||||||||||||||||||
2 cos zdz |
16 |
|
sin2 z |
cos2 zdz |
16 |
1 |
|
sin2 2zdz |
4 |
|
1 |
|
1 |
|
cos 4z dz |
|||||||||||||||||||||||||||||||||||||||||||
4 |
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
dz |
2 cos 4zdz |
2z |
|
1 |
sin 4z |
|
C |
|
2z |
sin 2z |
cos 2z |
|
C |
|
2z 2 sin z |
||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
||||||||||||||||||||||||||||
cos z 1 2 sin2 z |
|
|
|
|
|
C |
2 arcsin |
2 |
|
|
4 |
|
|
x2 |
1 |
2 |
|
|
C |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|||||||||
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 arcsin |
|
|
4 x2 2 |
|
x2 |
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
28

ГЛАВА 3
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§1. Задача о площади криволинейной трапеции
Пусть |
y f x – |
непрерывная положительная функция, |
заданная |
||||||||
на отрезке |
a,b . Фигура, ограниченная кривой |
y |
f x , прямыми x=a |
||||||||
и x=b и осью ОХ, называется криволинейной трапецией (рис.1). |
|
||||||||||
|
|
|
|
|
Поставим перед собой задачу вы- |
||||||
y |
y |
f |
x |
числить площадь криволинейной тра- |
|||||||
|
|
|
|
пеции. Для этого разобьем отрезок |
|||||||
|
|
|
|
a,b произвольным образом на n час- |
|||||||
|
|
|
|
тей. Абсциссы точек деления обозна- |
|||||||
|
|
|
|
чим |
a |
x0 |
x1 |
x2 |
xn 1 xn |
b . |
|
|
|
|
|
Получим |
n |
малых |
отрезков |
||||
|
|
|
|
x0;x1 , x1;x2 , , |
xn 1;xn . Обозначим их |
||||||
0 a |
|
b |
x |
длины соответственно |
x1 , |
x2 ,..., |
xn |
||||
|
Рис. 1 |
|
|
xi |
xi |
xi-1 . |
|
|
|
|
|
Проведя через точки деления прямые, параллельные оси OY, мы разобьем криволинейную трапецию на n малых криволинейных трапеций. Площадь всей криволинейной трапеции S равна сумме площадей всех малых криволинейных трапеций
(рис.2):
|
n |
S ΓS1 ΓS2 ΓSn , или S |
ΓSi |
|
i 1 |
y |
y f x |
x
0 x0=a ξ1 x1 ξ2 x2 |
xn-1 ξn b=xn |
Но вычислить площади малых криволинейных трапеций не проще, чем площадь большой. Поэтому поступим следующим образом. В каждом из от-
резков |
xi 1; xi |
выберем |
произвольную |
точку |
|
ξi xi 1 |
ξi xi |
и каждую |
|
Рис. 2 |
малую |
криволинейную |
|
|
трапецию заменим прямо- |
|
угольником с тем же основанием xi 1; xi |
и высотой, |
равной f ξi . |
|
Получим Si |
f ξi xi – площадь каждой малой |
криволинейной |
|
29

трапеции приближенно равна площади прямоугольника, а площадь всей криволинейной трапеции приближенно равна площади получившейся
|
n |
ступенчатой фигуры: S |
f ξi xi |
i |
1 |
Очевидно, чем меньше длины отрезков xi , тем меньше погреш-
ность этого приближенного равенства, поэтому естественно за точное значение площади криволинейной трапеции принять предел площадей ступенчатых фигур при условии, что наибольшая из длин отрезков разбиения стремится к нулю (следовательно, число отрезков разбиения n стремится к бесконечности):
|
|
n |
|
S |
lim |
f i xi |
(1) |
|
n |
0 i 1 |
|
|
max x |
|
|
|
i |
|
|
§2. Определение определенного интеграла
К нахождению предела сумм, аналогичных сумме (1), приводит целый ряд задач естествознания. Поэтому вполне естественно изучить этот процесс независимо от конкретного содержания задачи.
|
|
Пусть на отрезке |
a,b |
задана функция y f |
x |
. Выполним сле- |
||||||||||
дующие действия. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1.С помощью точек деления |
x1 |
x2 |
... |
xn 1 |
|
разобьем отрезок |
||||||||
a,b |
на |
n |
“малых” |
отрезков |
|
x0;x1 , |
x1;x2 , , xn 1;xn , |
где |
||||||||
x0 |
|
a, xn |
b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.В каждом из малых отрезков |
xi 1; xi |
i |
1, 2, ..., n выберем |
|||||||||||
произвольную точку |
ξi , |
xi 1 |
ξi |
|
xi , |
и умножим значение функции |
||||||||||
f |
x |
в точке |
i на длину |
xi |
xi |
xi 1 |
соответствующего отрезка: |
|||||||||
f |
ξi |
xi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Составим |
сумму |
|
ζn |
|
всех |
|
таких |
произведений: |
||||||
ζn |
f |
ξ1 |
x1 |
f ξ2 x2 |
f |
ξn |
xn , или |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζn |
|
f |
ξi |
xi |
|
|
|
(2) |
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
Сумма вида (2) называется интегральной суммой для функции |
||||||||||||||
f |
x |
на отрезке |
a,b . |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4.Наибольшую |
из |
длин |
малых |
отрезков |
обозначим |
λ |
||||||||
λ |
|
max |
x1, x2 , , |
xn |
и назовем ее шагом разбиения. Пусть число |
|||||||||||
30

отрезков разбиения неограниченно растет |
n |
и |
0 . Если при |
||||||||
этом интегральная сумма ζ n |
имеет конечный предел, который не зави- |
||||||||||
сит ни от способа разбиения отрезка |
a,b |
на малые отрезки, ни от вы- |
|||||||||
бора точек |
i |
в каждом из них, то этот предел называется определенным |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
интегралом от функции |
f x |
на отрезке |
a,b и обозначается f x dx. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
n |
|
|
|
|
|
Таким образом, |
f |
x dx |
lim |
f |
ξi |
xi. |
|
|
|||
|
|
|
a |
|
|
λ 0 i 1 |
|
|
|
|
|
Числа a и b называются соответственно нижним и верхним преде- |
|||||||||||
лами интегрирования, |
f |
x – подынтегральной функцией, x – перемен- |
|||||||||
ной интегрирования, |
a,b – отрезком интегрирования (или областью |
||||||||||
интегрирования). |
|
|
|
|
|
|
|
|
|
||
Функция f x , |
для которой на отрезке |
a,b |
существует определен- |
||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
ный интеграл |
f |
x dx, |
называется интегрируемой на этом отрезке. |
||||||||
a
Имеет место теорема существования определенного интеграла. Всякая непрерывная на отрезке a,b функция интегрируема на
этом отрезке.
Возвращаясь к §1, отметим факт, выражающий геометрический смысл определенного интеграла: определенный интеграл от неотрицательной непрерывной функции численно равен площади криволинейной
трапеции, ограниченной кривой y |
f x , |
прямыми x a и x b и |
||
|
b |
|
|
|
осью OX. |
f |
x dx |
|
Sкр.тр. |
|
a |
|
|
|
Замечания. |
|
|
|
|
1.Определенный интеграл не зависит от обозначения переменной |
||||
b |
b |
b |
|
|
интегрирования: f x dx |
f z dz |
f |
t dt и т.д. |
|
a |
a |
a |
|
|
|
|
a |
|
|
2.Будем полагать по определению: |
f |
x dx 0 |
||
a
31

3.При введении понятия определенного интеграла мы полагали
|
|
|
|
b |
|
a |
|
a b . В случае b |
a примем по определению: f |
x dx |
f |
x dx |
|||
|
|
|
|
a |
|
b |
|
§3. Свойства определенного интеграла |
|
|
|||||
b |
|
b |
b |
|
|
|
|
1. f x g x |
dx |
f x dx |
g x dx |
|
|
|
|
a |
|
a |
a |
|
|
|
|
|
|
|
|
|
b |
|
b |
|
|
y |
f |
2. |
kf x dx |
k |
f x dx, |
|
|
|
a |
|
a |
||
|
|
|
|
|
|
||
где k=const.
0 |
a |
c |
b |
x |
|
|
Рис. 3 |
|
|
3.Если отрезок интегрирования |
a,b разбит на две части a,с и |
|||
|
b |
c |
b |
|
c,b , то |
f x dx |
f x dx |
f x dx |
– свойство аддитивности. |
|
a |
a |
c |
|
y f 
0 |
a |
b |
x |
Рис. 4
f x g x , то
g x , то
Геометрически это значит, что площадь криволинейной трапеции с основанием a,b равна сумме площадей криволинейных трапеций с основаниями a,с и c,b (рис.3).
4.Если |
на |
отрезке |
a,b |
|
b |
|
|
f x 0, то |
f |
x dx 0. |
|
|
a |
|
|
5.Если |
на |
отрезке |
a,b |
32
