
Курс лекций по высшей математике. 2 часть
.pdf
Можно показать что ряд (8) имеет область сходимости 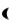 1;1 . Пример 4. Разложить в степенной ряд функцию f (x) arctgx . Проинтегрируем обе части разложения (7) от 0 до x при x
1;1 . Пример 4. Разложить в степенной ряд функцию f (x) arctgx . Проинтегрируем обе части разложения (7) от 0 до x при x  1;1 :
1;1 :
x |
dt |
x |
|
|
|
|
|
1 n x2n |
|
|
|
|
|
1 x2 |
x4 x6 ...... |
... dx или |
|
||||||||
|
|
|
||||||||||
0 1 x2 |
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x3 |
|
x5 |
... ( 1)n |
x 2n 1 |
|
|||
|
|
arctgx |
x |
|
|
|
|
|
|
... |
(9) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
5 |
|
|
2n |
1 |
|
||
Можно показать, что ряд (9) |
имеет область сходимости |
1;1 . |
||||||||||
6. Применение рядов к приближенным вычислениям
Числовые и функциональные ряды широко применяются в приближенных вычислениях. Рассмотрим это на примерах.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x2 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 1. Вычислить |
e |
с точностью до 0,001. |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Воспользуемся |
|
|
|
|
|
|
|
|
|
|
полученным |
|
|
|
|
|
разложением: |
|||||||||||||||||||||||||
e x |
2 |
|
|
|
|
x |
2 |
|
|
x |
4 |
|
|
x |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
... . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1! |
|
|
2! |
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
x |
2 |
|
|
|
|
1 |
|
|
|
x |
2 |
|
x |
4 |
|
|
x |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Тогда: |
|
|
e |
dx |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
... dx |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
|
0 |
|
1! |
2! |
|
|
3! |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
|
x3 |
|
|
|
x5 |
|
|
|
|
x7 |
|
|
|
|
x9 |
|
|
|
|
x11 |
|
|
|
1 |
1 1 |
1 |
1 |
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3 |
|
|
|
10 |
|
|
|
|
42 |
|
|
|
9 |
4! |
|
11 5! |
|
0 |
|
3 |
10 |
42 |
216 |
1320 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0,3333 0,1 0,0238 0,0046 0,0008 0,7475 0,748
Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит
0,001.
Пример 2. Вычислить 3 10 с точностью до 0,001.
10 с точностью до 0,001.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
8 10 |
|
|
|
|
|
|
2 |
|
|
|||
3 10 |
|
|
|
2 |
3 1 |
2 (1 0,25) 3 |
. Используем биномиальный |
||||||||||
|
|
|
|
||||||||||||||
|
|
|
8 |
|
|
|
|
|
|
8 |
|
|
|
|
|
||
ряд: x |
0,25 , |
m |
|
1 |
. |
|
|
|
|
|
|
||||||
3 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
103

|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
( |
1 |
|
1) |
|
|
|
1 |
|
( |
1 |
1) ( |
1 |
2) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0,25 |
3 |
|
3 |
|
0,252 |
|
3 |
|
3 |
3 |
0,253 |
||||||||||
3 10 |
2 |
(1 |
|
|
|
|
|
|
|
||||||||||||||||||||||
3 |
|
|
|
|
|
2! |
|
|
|
|
|
|
|
3! |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
1 |
|
1 |
1 |
2 |
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
3 |
|
3 |
|
3 |
|
0,254 ) 2 |
|
1 |
|
0,0833 |
|
0,0069 0,00096 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
4! |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
1 |
|
0,0833 |
0,0069 |
|
|
2,1528 |
2,153 |
|
|
|
|
|
|
|
|
|
|||||||||||||
Так как ряд знакочередующийся и 0,00096<0,001, то все слагаемые, начиная с 0,00096, отбрасываем и при этом погрешность не превосходит
0,001.
Пример 3. Вычислить e0,1 с точностью до 0,001. Для функции e x формула Тейлора имеет вид:
|
|
|
|
|
e x |
1 |
|
|
x |
|
|
x 2 |
... |
|
|
xn |
R (x) , где R |
|
( x) |
|
x n |
1 |
|
ec , c |
0; x . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
n! |
n |
|
|
|
|
|
(n 1)! |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
При |
|
|
x |
|
|
0,1 |
получаем |
|
знакоположительный |
|
числовой |
ряд; |
|||||||||||||||||||||||||||||
c |
0;0.1 . 0.1 |
|
|
|
0;0,5 , поэтому |
0 |
c |
0,1 |
0,5 и |
ec |
|
|
e0,5 |
2 . |
Тогда |
|||||||||||||||||||||||||||||||
|
Rn (x) |
|
|
|
|
x |
|
n 1 |
|
|
|
ec |
2 |
|
x |
|
n 1 |
. Необходимо взять столько членов ряда, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
(n |
1)! |
|
|
|
(n |
1)! |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
n 1 |
|
|
||||||||||||||||||||
чтобы |
|
выполнялось |
|
|
|
|
условие |
|
|
|
|
|
|
|
или |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Rn (x) |
|
(n |
1)! |
0,001 |
||||||||||||||||||||||||||||||||||||
|
|
x |
|
n 1 |
0,0005 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(n |
1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
При x |
0,1 получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
e0,1 |
1 |
|
0,1 |
|
|
0,1 2 |
0,1 |
3 |
1 |
0,1 |
0,005 |
|
0,0002 |
1,1052 |
1,105 . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Так как 0,0002<0,0005, то достаточно взять четыре слагаемых. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Пример |
|
|
4. |
|
Проинтегрировать |
дифференциальное |
уравнение |
||||||||||||||||||||||||||||||||||
|
y |
y |
x 2 , |
y(0) |
|
2 методом последовательного дифференцирования. |
||||||||||||||||||||||||||||||||||||||||
Будем искать решение в виде ряда Маклорена:
|
y(x) |
y 0 |
y 0 |
|
x |
y 0 |
x 2 ... |
y n |
0 |
x n ... . |
|
|
1! |
|
2! |
n! |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
y |
y x 2 , |
y |
y |
2x , y |
y 2 , y 4 |
y 5 , ... , y n |
y 3 |
||||
при n |
4, 5, ... . |
|
|
|
|
|
|
|
|
|
|
104

При |
x |
0 |
получаем: |
y(0) |
2 , |
y 0 |
2 , |
y (0) |
2 , |
y n (0) |
0 при n |
3, 4, 5, ... . Окончательно получаем |
|
|
|
||||
y x |
2 |
2x |
x 2 . |
|
|
|
|
|
|
§3. Ряды Фурье
1. Разложение в ряд Фурье функций с периодом 2
Многие процессы, происходящие в природе и технике, обладают свойством повторяться через определѐнные промежутки времени. Такие процессы называются периодическими. Периодические процессы описываются периодическими функциями. Простейшими периодическими
функциями с периодом |
2 являются sin x |
и cos x . Легко показать, |
||||||||||||||||||||
что функции sin wx и cos wx имеют период |
|
2 |
. |
|
|
|||||||||||||||||
w |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим несколько интегралов, которые нам понадобятся в даль- |
||||||||||||||||||||||
нейшем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k и n–натуральные числа |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
cosnxdx |
cosnxdnx |
sin nx |
|
|
0. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
sin nxdx |
|
sin nxdnx |
|
cosnx |
|
0. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
n |
|
1 |
|
|
n |
|
|
|
|
|
|
0, n |
k |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
cos k x cos nk dx |
cos(k n)x |
|
|
cos(k |
n)x dx |
|||||||||||||||||
|
|
|
|
|
|
|
, n |
k |
||||||||||||||
2 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
sin k x sin nxdx |
1 |
|
cos(k |
|
|
|
n)x |
|
cos(k |
n)x dx |
0, n |
k |
||||||||||
|
|
|
|
|
|
|
|
|
, n |
k |
||||||||||||
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
sin k xcosnxdx |
1 |
|
|
|
sin(k |
|
n)x |
sin(k |
|
n)x dx 0. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим функциональный ряд вида
105

|
a0 |
a1 cos x b1 sin x |
a2 cos 2x |
b2 sin 2x |
|
||||
2 |
|||||||||
|
|
|
|
|
|
(1) |
|||
|
|
|
|
|
a0 |
|
|||
|
an cos nx |
bn sin nx |
|
an cos nx bn sin nx . |
|||||
|
2 |
|
|||||||
|
|
|
|
|
|
n 1 |
|
||
Этот ряд |
называется |
тригонометрическим |
рядом, а числа |
||||||
a0 , a1 ,b1 , a2 ,b2 , , an ,bn , –коэффициентами тригонометрического
ряда. |
|
|
|
|
|
Если ряд (1) сходится к функции f (x) , то функция |
f (x) |
являет- |
|||
ся периодической с периодом 2 |
. Поэтому будем рассматривать сумму |
||||
ряда f (x) в любом интервале длины 2 , например, |
; |
. Будем |
|||
считать, что функция f (x) есть сумма ряда (1): |
|
|
|||
f (x) |
a0 |
an cos nx bn sin nx |
(2) |
||
2 |
|
||||
|
|
n 1 |
|
|
|
Предположим, что ряд (2) можно почленно интегрировать в пределах от –  до
до  , сделаем это.
, сделаем это.
f (x)dx |
|
|
a0 |
dx |
|
(a |
|
cosnxdx b |
sin nxdx) . |
||||
|
|
|
|
||||||||||
|
|
2 |
|
|
|
n |
|
|
n |
|
|
||
|
|
|
|
|
n 1 |
|
|
|
|
|
|||
cos nxdx |
0 |
|
|
|
и |
|
|
sin nxdx |
0 , |
поэтому |
|||
f (x)dx |
a0 |
dx |
a |
|
, откуда |
|
|
|
|||||
2 |
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
a0 |
|
|
|
f (x)dx . |
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|||
Умножим обе части равенства (2) на coskx и проинтегрируем по- |
|||||||||||||
лучено равенство от – |
до . |
|
|
|
|
|
|||||||
f (x) cos kxdx |
|
a0 |
cos kxdx |
|
|
||||||||
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
an |
cos nx cos kxdx |
bn sin nx cos kxdx |
|
||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
106

|
|
Учитывая, |
что |
|
|
cosk xdx |
0, |
sin nx cosk xdx 0, |
||||||||
|
cos nxcos k xdx |
0, n |
k |
|
|
|
|
|
|
|
|
|
||||
|
, n |
k , |
|
|
|
|
|
|
|
|
|
|||||
|
|
получаем |
|
f (x) cos k xdx |
ak |
. |
Отсюда |
|||||||||
ak |
1 |
|
f (x) cos k xdx. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Переобозначая k на n , получаем |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
an |
1 |
|
f (x) cos nxdx. |
(4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Аналогично, умножая обе части равенства (2) на sin kx и интегри- |
||||||||||||||
руя от – до , получим |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
bn |
1 |
|
|
f (x)sin nxdx. |
(5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Определение: |
|
|
Тригонометрический |
ряд |
||||||||||
|
a0 |
|
|
|
an cosnx |
bn sin nx , коэффициенты которого вычисляют- |
||||||||||
2 |
|
n 1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ся по формулам (3), (4), (5), называется рядом Фурье, соответствующим
функции f (x) , а числа a0 , an ,bn , n |
1,2, , называются коэффици- |
ентами Фурье. |
|
Мы предполагали, что функция |
f (x) является суммой тригоно- |
метрического ряда, который можно почленно интегрировать от – до
до
. Какова область сходимости построенного ряда Фурье? Сходится ли он к функции f (x) ? Ответы на эти вопросы даѐт следующая теорема.
Теорема Дирихле:
Пусть периодическая функция f (x) с периодом 2 на любом отрезке [ a;b ] удовлетворяет условиям:
1)функция непрерывна на [ a;b ] или имеет на нѐм конечное число точек разрыва I рода;
107

2)функция кусочно–монотонная на [ a;b ]. Тогда ряд Фурье, соответствующий этой функции, сходится во всех точках числовой оси. При этом в каждой точке непрерывности функции f (x) сумма ряда Фурье
S (x) |
совпадает с f (x) . В каждой точке x0 |
||||||||
f (x) |
имеем: S (x0 ) |
1 |
|
lim f (x) |
|
lim |
|||
|
|
|
|
||||||
2 |
|
||||||||
|
|
|
x x0 |
|
|
x x0 |
|||
Пример: Разложить в ряд Фурье функцию |
|||||||||
периодом 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ao |
|
1 |
xdx |
1 |
|
x2 |
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
разрыва I рода функции
f (x) .
f (x) x на (–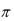 ;
; ] с
] с
0
|
|
|
|
|
|
a |
1 |
|
|
x cosndx |
1 |
|
x |
1 |
|
sin nx |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
udv |
uv |
vdu |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
sin nxdx |
|
|
1 |
|
|
|
sin n |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
u |
|
x, dv cosnxdx |
|
|
|
|
|
|
1 |
|
|
|
sin n |
|
1 |
|
cosnx |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
du |
|
dx,v |
cosnxdx |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
n |
2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
sin nx |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
(cosn |
|
cosn |
) 0. |
|
||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
b |
1 |
xsin nxdx |
|
1 |
x( |
|
1 |
cosnx) |
|
|
|
1 |
|
|
cosnxdx |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
u x, dv |
sin nxdx, du |
|
|
dx |
|
|
|
|
|
|
|
|
2 |
|
|
cosn |
|
|
1 |
|
sin nx |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n2 |
|||||||||||||||||||||||||||
v |
sin nxdx |
|
1 |
cosnx |
|
|
2 |
|
|
|
|
|
n |
|
|
|
n 1 |
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
1) |
|
|
( |
1) |
|
|
|
|
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||
Получаем f (x) ~ |
( |
1) |
n 1 2 |
|
sin nx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Замечание: Нетрудно показать, что если функция |
f (x) имеет пе- |
||||||||||||||||||||||||||||||||||||||||
риод 2 |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
108

|
2 |
f (x)dx |
f (x)dx , где –любое число. Этот факт можно ис- |
пользовать при вычислении коэффициентов Фурье.
2. Ряды Фурье для четных и нечетных функций
Отметим некоторые известные свойства чѐтных и нечѐтных функ-
ций. |
|
|
|
|
|
|
Если функции f (x) |
и |
(x) |
одновременно обе чѐтные или обе |
|||
нечѐтные, то их произведение |
f (x) |
(x) являются чѐтной функцией. |
||||
Если одна из функций f (x) и |
(x) чѐтная, |
а другая нечѐтная, то |
||||
их произведение f (x) |
(x) являются нечѐтной функцией |
|
||||
|
|
|
|
a |
|
|
Если f (x) –нечѐтная на [–a;a] функция, то |
f (x)dx 0 . |
|
||||
|
|
|
|
a |
|
|
Если |
f (x) –чѐтная |
на |
[ a; a] |
функция, |
то |
|
a |
a |
|
|
|
|
|
f (x)dx 2 f (x)dx . |
|
|
|
|
|
|
a |
0 |
|
|
|
|
|
Учитывая эти свойства, разложение в ряд Фурье чѐтной или нечѐтной функции упрощается.
Пусть функция f (x) –чѐтная и удовлетворяет теореме Дирихле. Тогда функции f (x)  cos nx –чѐтны, а f (x)
cos nx –чѐтны, а f (x)  sin nx –нечѐтные при любых n=1,2,... Поэтому
sin nx –нечѐтные при любых n=1,2,... Поэтому
a0 |
2 |
f (x)dx , an |
2 |
f (x) cos nxdx, bn |
0 . |
|
|
||||
|
|
||||
|
|
0 |
|
0 |
|
Ряд Фурье для чѐтной функции имеет вид:
|
f (x) ~ |
a0 |
an cosnx |
|
2 |
||
|
|
n 1 |
|
Пусть функция |
f (x) нечѐтная и удовлетворяет теореме Дирихле. |
||
Тогда функции f (x) |
cos nx –нечѐтные, а |
||
f (x)  sin nx –четные при любых n=1,2,... Поэтому
sin nx –четные при любых n=1,2,... Поэтому
a0 0 , an 0 , bn |
2 |
f (x) sin nxdx. |
|
||
|
||
|
|
0 |
Ряд Фурье для нечѐтной функции имеет вид:
109

|
f (x) ~ |
|
bn |
sin nx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример: |
Разложить |
в |
ряд |
Фурье |
|
функцию |
f (x) |
| x | |
при |
|||||||||||||||||||||||||||||||||||||||||||||||||
x |
( |
; |
|
|
] с периодом 2 |
. Данная функция четная, поэтому bn |
|
0 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
a0 |
|
2 |
|
|
|
xdx |
|
2 |
|
|
|
|
|
x2 |
|
|
|
, |
|
an |
|
2 |
|
|
x cos nxdx |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
2 |
|
|
1 |
|
|
|||||||||||
|
u |
x, dv |
|
cosnxdx, du |
|
dx |
|
|
|
x |
sin nx |
|
|
|
|
|
sin nxdx |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
0 |
|
|
0 n |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
v |
|
cos nxdx |
|
|
|
1 |
sin nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
( 1)n |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
0 |
|
|
|
|
|
cosnx |
|
|
|
|
|
1 . |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
0 |
|
|
|
n2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0, n |
2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Заметим, что an |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
, n |
2k |
1, k |
1,2, . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2k |
|
1)2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Получим ряд Фурье: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
| x |~ |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
cos(2k 1)x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
|
|
k |
1 (2k |
1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
3. Ряд Фурье для функции с периодом 2e |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Пусть функция |
|
|
f (x) имеет период 2e , где e |
0 –любое число. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сделаем замену переменной: |
|
x |
|
|
et |
, |
|
тогда функция |
|
f |
|
et |
|
|
(t) |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
имеет |
|
|
|
|
|
|
|
|
|
|
период |
|
|
|
|
2 . |
|
|
|
|
|
|
Действительно, |
||||||||||||||||||||||||||||||||||||
f |
e(t |
2 |
) |
|
|
|
|
f |
|
|
|
et |
2e |
|
f |
|
|
|
et |
. |
|
Разложим функцию |
(t) |
в |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
ряд Фурье, считая что она удовлетворяет теореме Дирихле. Получим |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(t) |
|
|
f |
|
et |
|
~ |
|
a0 |
|
|
|
|
|
an cosnt |
|
bn sin nt |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
110

где |
|
|
|
a0 |
1 |
f |
et |
|
dt , |
an |
1 |
|
f |
et |
cos ntdt , |
||||
|
|
|
|
|
|
|
|
|
|
||||||||||
b |
1 |
f |
et |
|
sin ntdt . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возвратимся |
к |
прежней |
переменной: t |
x |
, |
dt |
|
|
dx , x – |
|||||||||
|
|
|
|
||||||||||||||||
|
e |
|
e |
||||||||||||||||
изменяется от e до e , если t изменяется от 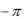 до
до  . Ряд Фурье имеет вид:
. Ряд Фурье имеет вид:
|
|
f (x) ~ |
a0 |
|
|
|
|
|
|
an cos |
nx |
|
|
bn |
sin |
nx |
|
|
|
, |
|
|
|
|
||||||||||||||||
|
|
2 |
|
n 1 |
|
|
|
e |
|
|
|
e |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
a0 |
|
|
1 e |
f (x)dx , |
|
|
|
|
|
|
1 e |
|
|
nx |
|
||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|
f (x) cos |
|
dx , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
e |
e |
|
|
|
e |
e |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
||||||||
|
|
|
1 e |
|
|
|
|
|
|
|
nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
b |
|
|
|
|
|
f (x) |
sin |
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
n |
|
e e |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Если функция |
f (x) –чѐтная с периодом 2e , то a0 |
2 e |
f (x)dx , |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
e 0 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 e |
|
|
|
|
|
|
nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a |
n |
|
|
|
|
f (x) cos |
|
|
|
|
|
dx , |
|
b |
|
|
0 . |
Ряд Фурье для четной функции |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
e 0 |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) ~ |
a0 |
|
|
|
|
an |
cos |
|
nx |
|
|
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
n 1 |
|
e |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Если |
функция |
|
|
f (x) –нечѐтная |
с |
периодом 2e , |
то |
a0 |
0 , |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 e |
|
|
|
|
|
|
|
nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
n |
|
0 , b |
|
|
|
|
|
f (x) sin |
|
|
|
|
|
|
dx . Ряд Фурье для нечѐтной функции |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
e 0 |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
имеет вид: |
|
f (x) ~ |
|
|
|
b sin |
nx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Пример. Разложить в ряд Фурье |
функцию |
f (x) |
|
x |
4 |
при |
||||||||||||||||||||||||||||||||
x |
|
( 4;4] с периодом 2e |
|
8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
111

|
|
|
|
|
|
a0 |
1 4 |
|
|
x |
|
|
|
4 dx |
1 |
|
|
|
(x |
4)2 |
|
|
4 |
|
|
|
|
|
8 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
n x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
nx |
|
|
|
4 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
a |
|
(x |
|
4)cos |
dx |
|
|
(x |
4) |
|
|
sin |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
n |
4 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
4 |
|
|
|
4 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
u |
x |
|
4;dv |
cos |
nx |
|
|
|
dx;du |
|
|
|
dx |
|
|
|
1 4 |
|
4 |
|
sin |
nx |
|
|
|
dx |
|
0 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 4 n |
|
4 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
nx |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
nx |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
nx |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||||||||||||
v |
cos |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
||||||||||||||||||
|
|
4 |
|
|
|
n |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 2 |
|
4 |
|
|
|
4 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
nx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
nx |
|
|
|
4 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
b |
|
|
|
|
(x |
4) sin |
|
|
|
|
dx |
|
|
|
|
(x |
4) |
|
cos |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
n |
4 4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
u x |
4; dv |
sin |
|
nx |
|
|
dx; du |
|
|
|
dx |
|
|
|
|
|
1 |
|
|
4 4 |
cos |
|
nx |
|
dx |
|
|
|
8 |
cos n |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
n |
|
|
|
|
4 |
|
|
|
|
|
n |
|
||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
v |
sin |
nx |
|
|
dx |
|
|
4 |
|
cos |
|
nx |
|
|
|
|
|
4 |
|
sin |
nx |
|
|
|
|
4 |
|
|
|
8( |
|
1)n 1 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
2 |
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
n |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Получаем ряд Фурье: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
x |
4 ~ |
4 |
|
|
8 |
|
|
|
|
( |
|
|
1)n |
1 |
sin |
nx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
n |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4. Разложение в ряд Фурье непериодических функций |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если функция |
|
f (x) |
задана на всей числовой оси и непериодиче- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ская, то еѐ нельзя разложить в ряд Фурье, так как сумма тригонометрического ряда является периодической функцией.
Рассмотрим |
непериодическую непрерывную функцию |
f (x) на |
||||
промежутке ( e; e] |
и построим ряд Фурье, который имел бы еѐ своей |
|||||
суммой в |
этом |
интервале. Для этого рассмотрим вспомогательную |
||||
|
__ |
|
|
|
__ |
|
функцию |
f (x) |
с |
периодом |
2e такую, |
что f (x) |
f (x) при |
|
|
|
|
|
__ |
|
x ( e; e] . Разложив в ряд Фурье функцию |
f (x) , мы получили тем |
|||||
самым разложение |
f (x) на ( |
e; e] . |
|
|
||
112
