
Курс лекций по высшей математике. 1 часть
.pdf
ГЛАВА I.
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
§1. Определители
1.1.Определители второго порядка
Определение. Выражение
|
a11 |
a12 |
a11 |
a22 |
a21 a12 называется определителем 2-го |
|
a21 |
a22 |
|||
порядка. |
|
|
|
|
|
Числа a11 , a12 , a21 , a22 |
– это элементы определителя. Определи- |
||||
тель 2-го порядка имеет две строки и два столбца. Индексы, стоящие внизу соответствующего элемента, означают номер строки и номер столбца определителя, на пересечении которых стоит указанный элемент. Например, элемент a12 стоит в первой строке и втором столбце
определителя.
Элементы a11 , a22 называют элементами главной диагонали опре-
делителя, а другие два элемента – соответственно элементами побочной диагонали.
Пример 1. Вычислим определитель
5 |
4 |
5 3 2 ( 4) 23 . |
|
2 |
3 |
||
|
1.2. Определители 3-го порядка
Определение. Выражение
a11 |
a12 |
a13 |
|
a22 |
a23 |
|
a21 |
a23 |
|
a21 |
a22 |
|
(1.1) |
|||
|
|
|
|
|||||||||||||
a |
|
a |
|
a |
|
a |
a |
a |
|
|||||||
|
21 |
|
22 |
|
23 |
11 |
a32 |
a33 |
12 |
a31 |
a33 |
13 |
a31 |
a32 |
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
|||
называется определителем 3-го порядка. Пример 2. Вычислить определитель:
1 |
2 |
1 |
|
3 |
4 |
2 |
. |
1 |
2 |
1 |
|
|
|
|
|
Решение. По определению получим:
|
1 |
4 |
2 |
2 |
3 |
2 |
1 |
3 |
4 |
1 (4 |
4) |
2 |
(3 |
2) |
|
|
2 |
1 |
|
1 |
1 |
|
1 |
2 |
|
|
|
|
|
1 |
(6 |
|
4) |
2 |
2 |
|
4. |
|
|
|
|
|
|
|
3
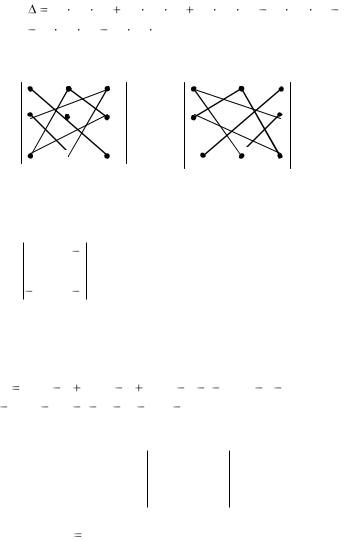
Если в формуле (1.1) раскрыть определители 2-го порядка и собрать слагаемые с одинаковыми знаками, то имеем:
a11 a22 a33 |
a21 a32 a13 |
a12 a23 a31 |
a31 a22 |
a13 |
(1.2) |
|
|
|
|
|
|
a11 a32 a23 |
a21 a12 a33. |
|
|
|
|
Элементы со знаком плюс и со знаком минус выбираются из определителя, как показано на рисунке:
Этот способ вычисления определителя 3-го порядка называется
правилом треугольника.
Пример 3. Вычислить определитель:
2 0 1 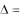 6 3 4 по правилу треугольника.
6 3 4 по правилу треугольника.
5 2 1
Решение. Перемножим элементы главной диагонали определителя, затем – элементы, лежащие на параллелях к этой диагонали, и элементы из противоположного угла определителя согласно правилу треугольника. Элементы, входящие в формулу (1.2) со знаком минус строим аналогично, но относительно побочной диагонали.
 2
2  3
3 ( 1) 6
( 1) 6  2
2  ( 1) 0
( 1) 0  4
4  ( 5) ( 5)
( 5) ( 5)  3
3 ( 1) 2
( 1) 2  4
4  2
2  6
6  0
0  ( 1)
( 1)  6 12 15 16
6 12 15 16 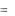 49.
49.
Замечание. Если применить правило треугольника к определителю треугольного вида
a11 a12 a13 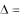 0 a22 a23 ,
0 a22 a23 ,
0 0 a33
то этот определитель будет равен произведению элементов главной диагонали, то есть  a11
a11  a22
a22  a33 .
a33 .
Определение. Минором элемента определителя 3-го порядка называется определитель 2-го порядка, получающийся из данного определителя вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
4

Минор элемента a ij , стоящего на пересечении i-й строки и j-го
столбца определителя, обозначают Мij. Например, для определителя
2 |
1 |
3 |
|
5 |
4 |
0 |
(1.3) |
6 |
2 |
7 |
|
|
|
|
|
миноры: M |
|
2 |
3 |
4, M |
|
1 |
3 |
12. |
22 |
6 |
7 |
31 |
4 |
0 |
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Определение. Алгебраическим дополнением элемента определителя 3-го порядка называется минор этого элемента, взятый со знаком плюс, если элемент стоит на пересечении строки и столбца с четной суммой номеров, и со знаком минус, если элемент стоит на пересечении строки и столбца с нечетной суммой номеров.
Алгебраическое дополнение элемента aij обозначают Aij . Согласно определению:
|
A |
( 1)i j |
M |
ij |
. |
|
|
ij |
|
|
|
|
|
Для определителя 3-го порядка знаки алгебраических дополнений |
||||||
определяются по таблице: |
|
|
|
|
|
|
|
+ |
- |
+ |
|
|
|
|
- |
+ |
- |
|
|
|
|
+ |
- |
+ |
|
|
|
|
|
|
|
|
|
|
Например, алгебраическое дополнение элемента a23 0 определителя (1.3) равно минору этого элемента, взятому со знаком минус:
A23 |
2 |
1 |
( 4 6) |
2 . |
|
6 |
2 |
||||
|
|
|
|||
|
|
|
|
|
Из определения определителя 3-го порядка вытекает, что
a11  A11 a12
A11 a12  A12 a13
A12 a13  A13 .
A13 .
Теорема разложения. Определитель 3-го порядка равен сумме парных произведений элементов какого-либо ряда определителя на их алгебраические дополнения (под рядом понимается строка или столбец).
Таким образом, имеет место шесть разложений:
5

a11 |
A11 |
a12 |
A12 |
a13 A13 , |
|
a21 |
A21 |
a22 |
A22 |
a23 A23 , |
|
a31 |
A31 |
a32 |
A32 |
a33 A33 , |
(1.4) |
a11 |
A11 |
a21 |
A21 |
a31 A31 , |
|
a12 |
A12 |
a22 |
A22 |
a32 A32 , |
|
a13 |
A13 |
a23 |
A23 |
a33 A33 . |
|
Можно доказать, что сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения элементов параллельного ряда равна нулю.
Пример 4. Вычислить определитель
1 2 3 2 1 2 ,
3 2 1
разлагая его по элементам второй строки. Решение. Согласно теореме разложения имеем:
2 |
2 |
3 |
1 |
1 |
3 |
2 |
1 |
2 |
2 (2 |
6) |
(1 |
9) |
2 (2 |
6) |
8 . |
|
2 |
1 |
|
3 |
1 |
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.3. Свойства определителей
Формулируя свойства, мы не будем указывать порядок определителя, так как эти свойства справедливы для определителей любого порядка, но доказательства свойств проведѐм для определителей 3-го порядка.
1.Определитель не меняет своего значения при замене всех его строк соответствующими столбцами, то есть
a11 |
a12 |
a13 |
|
a11 |
a21 |
a31 |
|
|
a21 |
a22 |
a23 |
|
a12 |
a22 |
a32 |
. |
(1.5) |
a31 |
a32 |
a33 |
|
a13 |
a23 |
a33 |
|
|
Действительно, разложим определитель слева по элементам первой строки, а определитель справа по элементам первого столбца. Тогда в обоих случаях согласно теореме разложения получим a11  A11 a12
A11 a12  A12 a13
A12 a13  A13 , что и доказывает неизменность определителя.
A13 , что и доказывает неизменность определителя.
Замечание. Определитель в правой части формулы (1.5) называют транспонированным по отношению к определителю в левой части этой формулы.
2.Если переставить две строки (столбца) определителя, то он изменит знак.
Пусть в определителе
6

a11 |
a12 |
a13 |
|
a21 |
a22 |
a23 |
, |
a31 |
a32 |
a33 |
|
например, переставлены первая и вторая строки. Тогда получим определитель
~ |
a21 |
a22 |
a23 |
|
||
a11 |
a12 |
a13 |
. |
|||
|
|
|||||
|
|
a31 |
a32 |
a33 |
|
|
Разложим определитель |
~ по элементам второй строки с учѐтом |
|||||
знаков, приписываемых алгебраическим дополнениям: |
||||||
|
+ |
- |
|
+ |
|
|
|
- |
+ |
|
- |
|
|
|
+ |
- |
|
+ |
|
|
|
|
|
|
|
|
|
Так как знаки миноров элементов второй строки противоположны зна-
кам миноров элементов первой строки, то |
|
|
|||
~ |
a11 |
( A11) a12 |
( A12 ) a13 |
( A13) |
. |
|
|||||
Следствие. Если две строки (столбца) определителя равны, то определитель равен нулю.
В самом деле, если в определителе
a11 a12 a13 a11 a12 a13 .
a31 a32 a33
переставить первую и вторую строки с одинаковыми элементами, то с одной стороны определитель не изменится, а с другой стороны – он поменяет знак, то есть 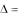
 , откуда
, откуда 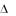 0 .
0 .
3.Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя.
Пусть дан определитель
~ |
K a11 |
K a12 |
K a13 |
|
|
a21 |
a22 |
a23 |
. |
||
|
|||||
|
a31 |
a32 |
a33 |
|
Разложим его по элементам первой строки. Тогда он будет равен: |
|||||
~ |
K a11 |
A11 |
K a12 A12 |
K a13 |
A13 |
|
|||||
|
K (a11 |
A11 |
a12 A12 |
a13 A13 ) |
K . |
Следствие 1. Если все элементы какого-либо ряда определителя равны нулю, то такой определитель равен нулю.
7

Следствие 2. Если элементы какого-либо ряда определителя пропорциональны элементам параллельного ряда, то определитель равен нулю.
Пусть, например, элементы первой и второй строк определителя пропорциональны. Тогда имеем
a11 |
a12 |
a13 |
|
a11 |
a12 |
a13 |
|
K a11 |
K a12 |
K a13 |
K |
a11 |
a12 |
a13 |
0 . |
a31 |
a32 |
a33 |
|
a31 |
a32 |
a33 |
|
4.Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель можно представить в виде суммы двух определителей, у которых все ряды, кроме данного, прежние, а в данном ряду в первом определителе стоят первые, а во втором – вторые слагаемые.
Допустим, что элементы первой строки определителя являются суммами двух слагаемых. Тогда имеем:
a11 |
b11 a12 |
b12 a13 |
b13 |
|
|
|
|
|
|
|
|
||
a21 |
a22 |
a23 |
|
|
|
|
|
|
|
|
|||
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|||
(a11 |
b11 ) |
A11 |
(a12 |
b12 ) A12 |
|
(a13 |
b13 ) |
A13 |
|||||
(a11 |
A11 |
a12 |
A12 |
a13 A13 ) |
(b11 A11 |
b12 |
A12 b13 A13 ) |
||||||
|
|
|
a11 |
a12 |
a13 |
|
|
b11 |
b12 |
b13 |
|
||
|
|
|
a21 |
a22 |
a23 |
|
|
a21 |
a22 |
a23 |
, |
||
|
|
|
a31 |
a32 |
a33 |
|
|
a31 |
a32 |
a33 |
|
||
так как в первых скобках записано разложение по первой строке определителя с элементами a11 , a12 , a13 , а во вторых – разложение опреде-
лителя с элементами b11 , b12 , b13 .
5.Величина определителя не изменится, если к элементам какоголибо ряда определителя прибавить или отнять элементы параллельного ряда, умноженные на одно и то же число, то есть составить линейную комбинацию строк или столбцов.
Для доказательства этого рассмотрим определитель
a11 a12 a13 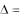 a21 a22 a23 .
a21 a22 a23 .
a31 a32 a33
Составим определитель, полученный из данного прибавлением к элементам его первой строки элементов второй строки, умноженных на число K.
8
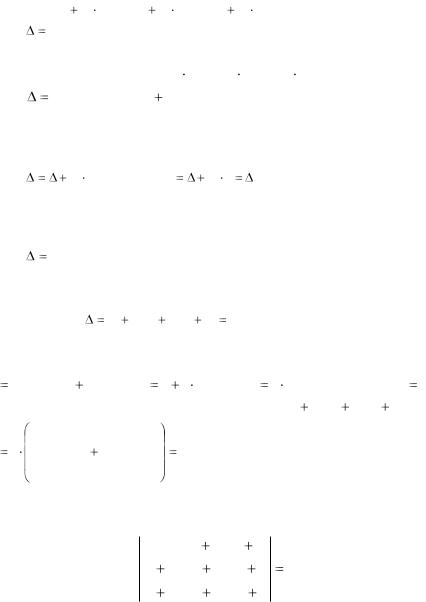
|
|
~ |
a11 |
|
K a21 |
a12 |
|
K a22 |
a13 |
K a23 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
a21 |
|
|
|
|
|
|
a22 |
|
|
a23 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
a31 |
|
|
|
|
|
|
a32 |
|
|
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
~ |
a11 |
|
a12 |
a13 |
|
|
K a21 |
|
K a22 |
|
K a23 |
|
|
|
|
|
|
||||||||||||||||
|
|
a21 |
|
a22 |
a23 |
|
|
|
a21 |
|
|
a22 |
|
a23 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
a31 |
|
a32 |
a33 |
|
|
|
a31 |
|
|
a32 |
|
a33 |
|
|
|
|
|
|
|||||||||||||
по свойству 4. Далее по свойству 3 и следствию 2 к нему получим |
|
|
|||||||||||||||||||||||||||||||||
|
|
~ |
|
|
|
|
|
a21 |
a22 |
a23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
K |
|
a21 |
a22 |
a23 |
|
|
K 0 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
a31 |
a32 |
|
|
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 5. Вычислить определитель |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4 |
5 |
|
6 |
|
, используя свойства определителей. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
7 |
8 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Решение. |
|
|
|
|
1 |
3 |
|
|
2 3 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
8 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1 |
2 |
3 |
|
|
|
3 |
|
3 |
3 |
|
|
0 |
|
3 |
1 |
1 |
1 |
|
3 |
|
1 |
|
1 |
|
1 |
|
|
|||||||
|
7 |
8 |
9 |
|
|
|
7 |
|
8 |
9 |
|
|
|
|
|
|
|
7 |
8 |
9 |
|
|
1 |
6 |
|
2 |
6 |
3 |
6 |
|
|||||
|
|
|
2 |
3 |
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
|
1 |
1 |
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
|
0 , |
так |
как у |
|
первого |
определителя, |
||||||||||||||
|
|
|
1 |
2 |
3 |
|
|
|
|
6 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стоящего в скобках, первая и последняя строки равны, а у второго – вторая и последняя строки пропорциональны.
Пример 6. Решить уравнение
x x 1 x 2
x 3 x 4 x 5 0 . x 6 x 7 x 8
Решение. Снова преобразуем определитель, используя свойство 4.
9

x |
x |
1 |
x |
2 |
|
|
x |
x |
1 |
|
x |
2 |
|
|
||||
x 3 x 4 x 5 |
|
x 3 x 1 3 x 2 3 |
|
|||||||||||||||
x 6 x 7 x 8 |
|
x 6 |
x 7 |
|
x 8 |
|
||||||||||||
|
|
x |
x |
1 |
x |
2 |
|
|
x |
|
x 1 |
|
x |
2 |
|
|
||
|
|
|
|
|
|
|
|
|||||||||||
|
|
x |
x |
1 |
x |
2 |
|
|
3 |
|
3 |
3 |
|
|
|
|
||
|
|
x 6 x 7 x 8 |
|
|
x 6 x 7 x 8 |
|
||||||||||||
|
|
|
|
|
x |
|
x |
1 |
x |
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
3 |
|
|
3 |
|
3 |
|
|
|
|
|
|
||
|
|
|
|
x |
6 |
x |
1 6 |
x |
2 |
6 |
|
|
|
|
|
|||
|
|
x |
x |
1 |
x |
2 |
|
|
|
x |
x |
1 |
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
3 |
3 |
|
3 |
|
|
|
3 |
|
3 |
3 |
|
0. |
||||
|
|
x |
x |
1 |
x |
2 |
|
|
6 |
|
6 |
6 |
|
|
|
|
||
Равенство нулю исходного определителя справедливо при любых значениях x, так как у первого определителя две строки равны, а у второгопропорциональны.
Таким образом, x ( , ) .
1.4.Определители 4-го порядка. Методы их вычисления
Определение. Выражение
|
a11 |
a12 |
a13 a14 |
|
|
|
|
a22 |
a23 |
a24 |
|
a21 |
a23 |
a24 |
||||
|
|
|
|
|
|
|||||||||||||
|
a21 |
a22 |
a23 |
a24 |
|
|
|
|
|
|||||||||
|
|
a11 |
|
a32 |
a33 |
a34 |
a12 |
a31 |
a33 |
a34 |
||||||||
|
a31 |
a32 |
a33 |
a34 |
|
|
||||||||||||
|
|
|
|
|
a42 |
a43 |
a44 |
|
a41 |
a43 |
a44 |
|||||||
|
a41 |
a42 |
a43 |
a44 |
|
|
a21 |
a22 |
a23 |
|
|
|
|
|
|
|||
|
|
a21 |
a22 |
a24 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a13 |
a31 |
a32 |
a34 |
|
|
a14 |
a31 |
a32 |
a33 |
|
|
|
|
|
|
|||
|
|
a41 |
a42 |
a44 |
|
|
|
|
a41 |
a42 |
a43 |
|
|
|
|
|
|
|
называется определителем 4-го порядка. Этот определитель можно за-
писать в виде: |
ai1 Ai1 |
ai2 Ai2 |
ai3 Ai3 |
ai4 Ai4 , |
(1.6) |
|||||
где A |
( 1)i j |
M |
ij |
, i |
1,2,3,4, |
j 1,2,3,4, |
M |
ij |
– это минор эле- |
|
ij |
|
|
|
|
|
|
|
|
||
мента, стоящего на пересечении i-ой строки, j-го столбца, Aij |
– его ал- |
|||||||||
гебраическое дополнение.
Формулу (1.6) можно записать короче с помощью значка суммиро-
|
4 |
|
вания : |
aij Aij , где i 1,2,3,4. |
(1.7) |
j |
1 |
|
10
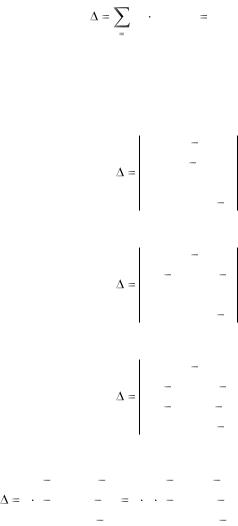
Формула (1.7) называется разложением определителя по i-й строке. Можно записать и разложение определителя по j-му столбцу:
4
aij Aij , |
j 1,2,3,4. |
(1.8) |
i 1
Ясно, что формулы (1.7) и (1.8) значительно упрощаются, если все элементы строки или столбца за исключением одного равны нулю.
Метод понижения порядка определителя основан на обращении всех, кроме одного, элементов определителя в нуль с помощью свойств определителей.
Пример 7. Вычислить определитель
2 3 3 4
2 |
1 |
1 |
2 . |
6 |
2 |
1 |
0 |
2 |
3 |
0 |
5 |
Решение. Умножая первую строку на –1, прибавим еѐ ко второй и четвѐртой строкам определителя. Имеем
2 3 3 4
0 2 2 2 .
6 2 1 0
0 0 3 9
Далее умножим первую строку на –3 и сложим еѐ с третьей стро-
кой:
2 |
3 |
3 |
4 |
|
0 |
2 |
2 |
2 |
. |
0 |
7 |
10 |
12 |
|
0 |
0 |
3 |
9 |
|
|
|
|
|
|
Полученный определитель разложим по элементам первого столбца и преобразуем его:
|
2 |
2 |
2 |
|
|
1 |
1 |
1 |
|
2 |
7 |
10 |
12 |
2 |
2 |
7 |
10 |
12 |
. |
|
0 |
3 |
9 |
|
|
0 |
3 |
9 |
|
|
|
|
|
|
|
|
|
|
|
Далее опять обращаем в нуль все элементы первого столбца, кроме одного, для чего умножим первую строку на –7 и прибавим ко второй строке, чтобы на месте элемента –7 получить нуль, а затем вычислим определитель второго порядка:
11

|
|
1 |
1 |
1 |
|
|
|
|
3 |
5 |
|
|
|
|
|
|
|||||
2 |
2 |
0 |
3 |
5 |
|
2 |
2 ( |
1) |
||
|
3 |
9 |
||||||||
|
|
0 |
3 |
9 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
4 |
( |
27 |
15) |
4 |
( |
12) |
48 . |
|
|
|
Метод приведения к треугольному виду заключается в таком преобразовании данного определителя, когда все элементы его, лежащие по одну сторону одной из его диагоналей, становятся равными нулю.
Пример 8. Вычислить определитель
1 |
1 |
1 |
1 |
|
|
1 |
1 |
1 |
1 |
приведением к треугольному виду. |
|
1 |
1 |
1 |
1 |
||
|
|||||
1 |
1 |
1 |
1 |
|
Решение. Вычтем первую строку определителя из остальных его строк. Тогда получим
1 |
1 |
1 |
1 |
|
0 |
2 |
0 |
0 |
. |
0 |
0 |
2 |
0 |
|
0 |
0 |
0 |
2 |
|
Этот определитель равен произведению элементов главной диагонали. Таким образом, имеем 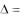 8 .
8 .
Замечание. Всѐ рассмотренное выше можно обобщить для определителей n-го порядка.
§2. Матрицы
2.1.Операции над матрицами
Определение. Матрицей размера m n называется прямоугольная
таблица из чисел aij , i 1,2,3, , m, |
j 1,2,3, , n, |
||||
|
a11 |
a12 |
a1n |
|
|
A |
a21 |
a22 |
a2n |
, |
|
|
|
|
|||
|
|
||||
am1 am2 amn
состоящая из m строк и n столбцов.
Матрица размера m m называется квадратной.
12
