
Курс лекций по высшей математике. 1 часть
.pdf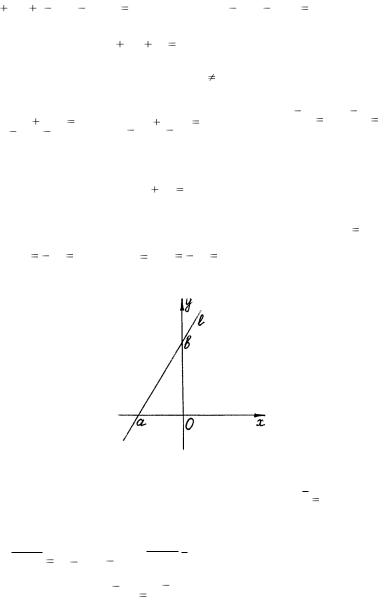
Раскрыв скобки и сгруппировав слагаемые |
в |
(2.12), |
|
получим |
|||||||||||||||||||||||
Ax By ( |
A x0 |
|
B y0) |
0 . |
|
Обозначим |
A x0 |
B y0 |
|
C , |
уравнение |
||||||||||||||||
примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Ax |
By |
|
C |
0 . |
|
|
|
|
|
|
|
(2.13) |
||||||||
(2.13) – общее уравнение прямой на плоскости. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
Если в уравнении (2.13) A , |
B , C |
0 , то, перенеся слагаемое С в |
|||||||||||||||||||||||||
правую часть и разделив на него обе части уравнения, получим |
|
|
|
||||||||||||||||||||||||
|
Ax |
By |
1 , |
или |
|
x |
|
|
|
|
|
y |
1 . |
Обозначим |
|
C |
a |
, |
|
C |
b , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
B |
||||||||
|
C |
C |
|
C |
|
|
|
|
|
C |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
||
тогда уравнение примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
1 |
|
|
|
|
|
|
|
(2.14) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(2.14) – уравнение прямой в отрезках, здесь a и b – отрезки, отсекаемые прямой на осях координат (рис. 21): из уравнения (2.13) при x 0 по-
лучим y |
C |
b , а при |
y 0 |
x |
C |
a . |
|
|
|
||||||
B |
A |
||||||
|
|
|
|
|
Рис. 21
Пусть M 0 (x0 ; y0) – заданная точка на прямой l , a (m, n) – век-
тор, параллельный прямой, его называют направляющим вектором прямой, и пусть M (x, y) – произвольная точка прямой l (рис. 22). Тогда
M0M ( x x0 ; y y0 ) , M 0 M 
 a
a 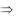
x x0 |
|
y y0 |
. |
(2.15) |
m |
|
n |
||
|
|
|
(2.15) – каноническое уравнение прямой, или уравнение прямой, проходящей через данную точку параллельно данному вектору.
53

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
В частности, |
если прямая |
l параллельна оси Ox , |
то ее направ- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ляющий |
вектор |
|
a |
( m,0 ) , |
|
и каноническое |
уравнение имеет |
вид |
|||||||||||||||||||||||||||||||||||
|
x |
x0 |
|
|
y |
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
Oy , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
, |
или y |
|
y |
0 |
. |
Если |
|
то |
|
a |
( 0,n ) , и каноническое |
|||||||||||||||||||||||||||||
|
|
|
m |
|
|
|
0 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
x0 |
|
y |
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
уравнение прямой |
|
|
|
|
|
, или x x . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Если в уравнении (2.15) величину отношения положить равной t |
||||||||||||||||||||||||||||||||||||||||
( t |
– параметр, переменная величина, |
t |
|
|
|
): |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
x |
x0 |
|
t , |
|
|
y |
|
|
y0 |
t , то, выразив x |
и y |
из уравнений, получим |
|||||||||||||||||||||||||||
|
|
|
|
|
m |
|
|
|
|
|
n |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
mt |
x0 , y |
nt |
|
y0 . |
|
|
|
|
|
(2.16) |
||||||||||||
(2.16) – параметрические уравнения прямой. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
Пусть на прямой l |
заданы две точки M 1 (x1 ; y1) |
и M 2 (x2 ; y2) . То- |
||||||||||||||||||||||||||||||||||||||
гда вектор |
|
|
|
|
|
(x2 x1; y2 |
y1) является направляющим вектором |
||||||||||||||||||||||||||||||||||||
|
M1 M 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
прямой и, используя уравнение (2.15), можно записать |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x1 |
|
|
|
y |
y1 |
|
. |
|
|
|
|
|
|
|
(2.17) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
x1 |
|
|
y2 |
y1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
(2.17) – уравнение прямой, проходящей через две данные точки. |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
Пусть |
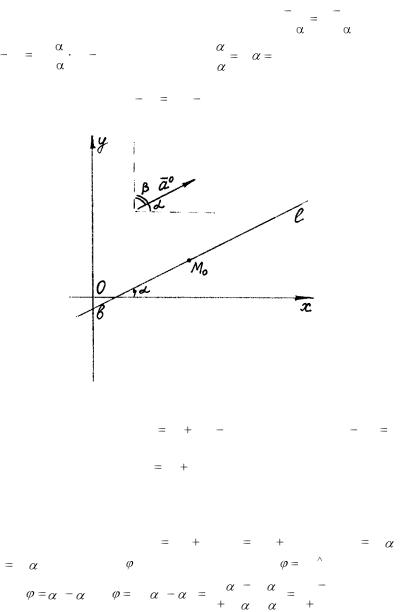
M 0 (x0 ; y0) – заданная точка на прямой l , |
|
|
|
– угол наклона |
|||||||||||||||||||||||||||||||||||
прямой к оси Ox , |
|
|
|
|
|
|
(рис. 23). В качестве направляющего вектора |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
возьмем единичный вектор |
|
0 . Координаты единичного век- |
||||||||||||||||||||||||||||||||||||||
прямой l |
a |
||||||||||||||||||||||||||||||||||||||||||
тора |
совпадают |
|
|
с |
его |
|
направляющими |
косинусами, |
поэтому |
||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||
|
a |
|
(cos |
|
; cos |
|
|
) , |
|
|
|
но |
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
sin |
|
a |
(cos |
;sin |
) . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используя |
уравнение |
(2.15), |
получим |
x |
x0 |
|
y y0 |
, или |
||||
cos |
|
sin |
||||||||||
|
|
|
|
|
|
|
|
|
||||
y y0 |
sin |
( x x0 ) . Обозначив |
sin |
|
tg |
k |
( k |
– угловой коэф- |
||||
cos |
cos |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
фициент прямой), получим уравнение |
|
|
|
|
|
|
||||||
|
|
y |
y0 k( x |
x0 ) . |
|
|
|
|
|
(2.18) |
||
|
|
|
|
|
|
|
Рис. 23 |
|
|
|
|
|
|
|
|
|
|||
Выразив из (2.18) |
y : |
y |
|
kx |
|
( y0 |
k x0) |
и обозначив y0 |
kx0 |
b , |
|||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
kx |
b . |
|
|
|
|
|
|
|
(2.19) |
|||
(2.18), (2.19) – уравнения прямой с угловым коэффициентом. В |
|||||||||||||||||||
уравнении (2.19) b – ордината точки пересечения прямой с осью Oy . |
|
||||||||||||||||||
Угол между двумя прямыми. Пусть прямые l1 и l 2 заданы соот- |
|||||||||||||||||||
ветственно |
уравнениями |
y |
|
k1x |
|
b1 , |
y |
k2 x |
|
b2 , |
где |
k1 tg |
1 , |
||||||
k 2 tg 2 . |
Обозначим |
|
угол между прямыми: |
|
|
(l1 |
l 2) |
(рис. 24). |
|||||||||||
Тогда |
|
|
, tg |
tg ( |
|
|
) |
tg |
2 |
tg |
1 |
|
k 2 |
k1 |
. |
|
|||
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
1 |
tg 1tg |
|
1 |
k1 k 2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
55

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg |
k 2 |
k1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.20) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Если l1 |
l 2 , то |
|
|
|
1 |
|
|
|
2 , а следовательно, tg |
1 |
|
tg |
2 , то есть k1= k2. |
||||||||||||||||||||||||||||
|
|
|
Если |
l1 |
l2 , |
то |
|
|
|
|
90 , |
tg |
|
не определен, |
ctg |
1 |
|
|
k1 k 2 |
0 , |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 2 |
k1 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
следовательно, |
1 |
|
|
k1 k 2 |
0 , или k 2 |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
k1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Если прямые l1 |
|
и l 2 заданы соответственно уравнениями |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
A1 x |
B1 y |
|
|
|
|
|
|
0 , |
|
|
A2 x |
B2 y |
|
|
|
|
0 , |
|
где |
|
|
|
|
|
|
(A1 , B1) , |
|||||||||||||||
|
|
|
|
C1 |
|
|
|
|
C2 |
|
|
|
n1 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
(A2 , B2) |
– |
нормальные векторы прямых, |
то cos |
|
|
|
n1 |
n2 |
|
, или |
|||||||||||||||||||||||||||||||
n2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
|
n2 |
|
|
||||
|
|
|
|
|
|
A1 A2 |
B |
|
B |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
cos |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
A12 |
B12 |
|
|
A22 |
|
|
B22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
A1 |
|
B1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Если l1 |
l 2 , то n1 |
n2 |
, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Если l1 |
l2 , n1 |
|
n2 |
0 , то есть |
A1 A2 |
B1 B2 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Расстояние от точки до прямой. Пусть прямая l |
на плоскости за- |
||||||||||||||||||||||||||||||||||||||||
дана |
уравнением |
|
Ax |
|
|
By C |
|
0 |
и |
|
точка |
|
|
M 0 |
имеет координаты |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
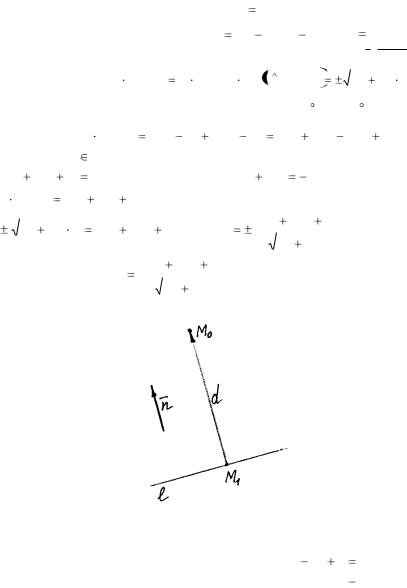
(x0 , y0) (рис. 25). Обозначим |
M 1 (x1, y1) – |
основание перпендикуляра, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
опущенного из точки M 0 на прямую l , |
|
d |
M1 M 0 , |
d – расстояние от |
||||||
|
|
|
|
|
|
|
||||
точки M 0 до прямой l . Тогда |
M1 M 0 |
(x0 |
x1; y0 |
y1) , а n (A; B) – |
||||||
нормальный вектор прямой. Рассмотрим скалярное произведение n  M1 M 0 .
M1 M 0 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С одной стороны, |
|
n M 1 M 0 |
|
n |
|
M 1 M 0 |
|
cos n |
M 1 M 0 |
|
|
|
A2 |
B2 d , |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
так как n |
|
M1 M 0 , |
следовательно, |
угол между ними 0 |
или180 |
. С дру- |
||||||||||||||||||||||||||||||||||||||
гой |
стороны, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B y0 (A x1 B y1) , |
||||||||||||||||||||||||||||
n M1 M 0 A(x0 |
|
x1) B( y0 |
y1) |
A x0 |
||||||||||||||||||||||||||||||||||||||||
но точка M 1 |
l , поэтому ее координаты удовлетворяют уравнению |
|||||||||||||||||||||||||||||||||||||||||||
|
Ax1 |
By1 |
C |
0 , |
|
|
|
|
|
|
откуда |
|
|
|
Ax1 By1 |
C , |
поэтому |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
n M 1 M 0 |
Ax0 |
|
|
By0 |
|
|
C . Приравнивая выражения, получим |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax0 |
|
By0 |
|
C |
или |
|
|
||||||||||||||||||
|
|
|
|
|
A2 B2 |
d |
|
|
Ax0 |
|
|
By0 C . Тогда d |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
Ax0 |
By0 |
|
C |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(2.21) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Рис. 25 |
|
Пример 12. Прямая l задана уравнением 2x 3y 6 |
0 . Соста- |
|
вить уравнения а) прямой l1 , |
проходящей через точку K (5; |
4) парал- |
лельно прямой l ; б) прямой |
l 2 , проходящей через начало координат |
|
перпендикулярно прямой l . |
|
|
57
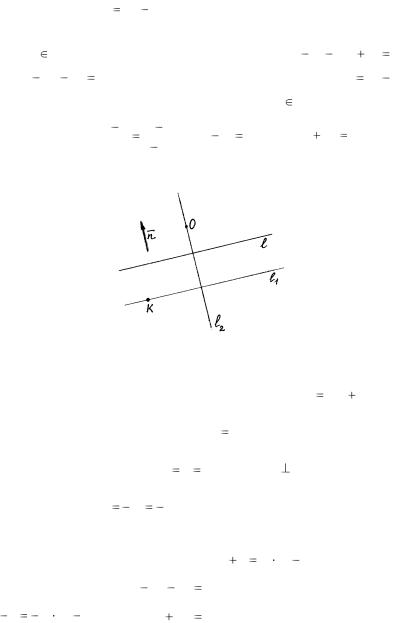
Решение. 1-й способ. Из уравнения прямой l определим нормальный
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вектор этой прямой n |
(2; |
|
|
3) . Этот вектор перпендикулярен и прямой |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
l1 (рис. |
26). Таким образом, для |
l1 известен нормальный вектор n |
и |
|||||||||||||||||
точка K |
l1 . Воспользуемся уравнением (2.12): 2(x |
5) 3( y |
4) |
0 |
||||||||||||||||
или 2x |
3y 22 |
0 – уравнение |
l1 . Для прямой l2 |
вектор |
|
|
|
|
||||||||||||
n |
(2; |
3) |
||||||||||||||||||
является |
направляющим |
|
|
|
|
|
и точка |
|
l2 . |
Воспользуемся |
||||||||||
( n |
l2 ) |
O( 0;0 ) |
||||||||||||||||||
уравнением (2.15): |
|
x |
0 |
|
|
y 0 |
, или 3x |
2y , или |
3x |
2y |
0 – урав- |
|||||||||
|
|
|
2 |
|
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
нение l2 .
|
|
|
|
|
Рис. 26 |
|
|
|
|
|||||
2-й способ. Запишем уравнение прямой l в виде |
y |
|
2 |
x 2 . Най- |
||||||||||
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
||||||
дем угловой коэффициент прямой l : |
k |
. Прямая |
l |
l , следователь- |
||||||||||
|
||||||||||||||
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
но, ее угловой коэффициент |
k1 |
k |
2 |
; прямая l2 l , поэтому ее угло- |
||||||||||
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вой коэффициент k 2 |
1 |
|
|
3 |
. Зная угловой коэффициент прямой и |
|||||||||
k |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
координаты точки на этой прямой, можно воспользоваться уравнением
(2.18). Получим уравнение прямой l |
: y |
4 |
2 |
(x 5) |
или, умножив |
|||||||
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
обе |
части |
на |
3, 2x 3y |
22 |
0 , |
и |
уравнение |
прямой l2 : |
||||
y 0 |
|
3 |
|
(x |
0) , то есть 3x |
2y |
0 . |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
58
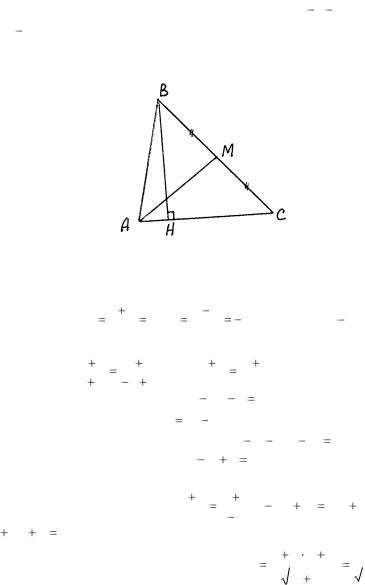
Пример 13. |
В треугольнике с |
вершинами A( 3; 2) , B(1; 4) , |
C(5; 6) составить уравнения медианы |
AM , высоты BH , найти длину |
|
высоты BH (рис. |
27). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Решение. M – середина отрезка BC , |
ее координаты найдем по |
||||||||||||||||||||||||||||||||
формулам (2.7): x |
1 |
5 |
|
3 , y |
4 |
6 |
|
|
|
1, то есть |
M (3; 1) . Таким |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
образом, на медиане известны две точки |
A и M . Воспользуемся урав- |
||||||||||||||||||||||||||||||||||
нением (2.17): |
x |
3 |
|
|
y |
2 |
|
, или |
x |
3 |
|
|
y |
2 |
|
– уравнение медианы |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3 |
3 |
|
|
1 |
2 |
|
|
|
|
|
6 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
AM . Его можно привести к виду x |
|
6y |
9 |
|
0 . Для составления урав- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
нения высоты BH |
найдем |
|
AC |
|
(8; |
4) |
|
– нормальный вектор прямой |
|||||||||||||||||||||||||||
ВН. Воспользуемся уравнением (2.12): 8(x |
1) |
|
4( y |
4) |
|
0 . Разделив |
|||||||||||||||||||||||||||||
на 4 и раскрыв скобки, получим 2x |
|
y |
2 |
|
0 – уравнение BH . Соста- |
||||||||||||||||||||||||||||||
вим уравнение прямой |
AC , используя уравнение (2.15) и рассматривая |
||||||||||||||||||||||||||||||||||
|
|
|
|
x |
3 |
|
y |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
AC как направляющий вектор: |
|
|
4(x |
3) |
|
8( y 2) , или |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x 2y 7 0 . Тогда длину высоты |
BH |
найдем по формуле (2.21) как |
||||||||||||||||||||||||||||||||
расстояние от точки B(1; 4 ) до прямой AC : d |
|
|
2 |
4 |
|
7 |
|
|
16 |
|
. |
||||||||||||||||||||||||
|
1 |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
2 |
2 |
|
5 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
§ 11. Кривые второго порядка
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат х, у.
59
Эллипс
Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
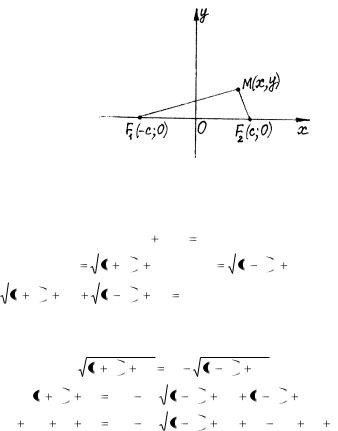
Обозначим фокусы F1, F2, расстояние между ними – 2с, постоянную из определения – 2а (по условию 2а > 2с, то есть а > с). Выберем декартову прямоугольную систему координат так, чтобы ось ОХ проходила через фокусы и точка О находилась на середине отрезка F1F2. В такой системе координат F1(-с; о), F2(с; о) (рис. 28).
Рис. 28
Выведем уравнение эллипса в выбранной системе координат. Для этого рассмотрим произвольную точку эллипса М(х, у).
По определению МF |
МF 2а. |
|
|
||||||
|
|
|
|
1 |
|
|
2 |
|
|
Но |
М F |
х |
с 2 |
у 2 |
, |
М F |
х с 2 у 2 , следовательно, |
||
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
х с 2 |
у 2 |
х |
с 2 |
у 2 |
|
2а. Преобразуем это уравнение, дважды |
|||
возводя в квадрат обе части:
х с
х 2 2хс с
|
х с 2 |
у 2 2а |
х с 2 |
у 2 ; |
|||||
|
|
|
|
|
|
|
|
|
|
2 |
у 2 |
4а 2 |
4а х |
с 2 |
у 2 |
х с 2 у 2 ; |
|||
|
|
|
|
|
|
|
|
|
|
2 |
у 2 |
4а 2 |
4а х |
с 2 |
у 2 |
х 2 2хс с 2 у 2 ; |
|||
60
4а х с 2 |
у 2 |
|
4а 2 |
|
4хс ; а х с 2 |
|
у 2 |
а 2 |
хс ; |
||||||||
а 2 |
х с 2 |
у 2 |
|
а 4 |
2а 2 хс х 2 с 2 ; |
|
|||||||||||
а 2 х 2 2а 2 хс а 2 с 2 |
|
а 2 у 2 |
а 4 |
|
2а 2 хс х 2 с 2 ; |
|
|||||||||||
|
а 2 |
с 2 х 2 |
а 2 у 2 |
а 2 а 2 с 2 . |
|
|
|
||||||||||
Обозначим а 2 с2 |
в2 |
|
0: в2 х 2 а 2 у2 |
а 2в2 . Разделив обе части |
|||||||||||||
на а2в2, получим каноническое уравнение эллипса: |
|
|
|
||||||||||||||
|
|
|
х 2 |
|
у |
2 |
1. |
|
|
|
|
|
|
|
|
(2.22) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
а 2 |
|
в2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Уравнение содержит только четные степени х, у, следовательно, |
|||||||||||||||||
кривая симметрична относительно осей координат. |
В первой коорди- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
натной четверти уравнение имеет вид |
у |
|
а |
2 |
х 2 , |
0 х а ; при |
|||||||||||
|
|
|
|||||||||||||||
|
а |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
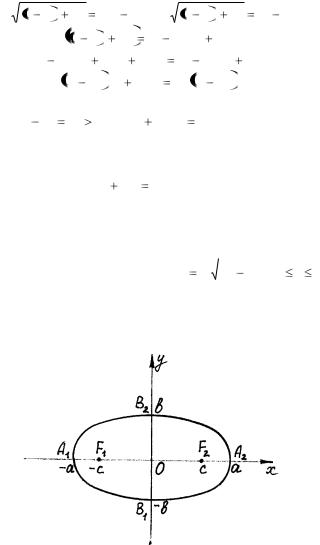
возрастании х от 0 до а у убывает от в до 0. Учитывая симметрию, можно сделать вывод о форме эллипса (рис. 29).
Рис. 29
Оси симметрии эллипса называются осями эллипса, точка их пересечения 0 – центром эллипса. Ось, на которой расположены фокусы, называется фокальной осью. Точки пересечения эллипса с осями назы-
ваются вершинами эллипса (А1, А2, В1, В2). Отрезки А1А2 и В1В2, а также их длины 2а и 2в называются соответственно большой и малой ося-
61
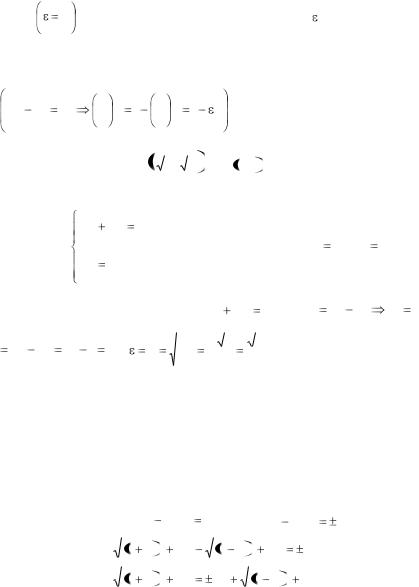
ми эллипса. Числа а и в называются соответственно большой и малой полуосями эллипса.
Отношение половины расстояния между фокусами к большой по-
луоси |
с |
называется эксцентриситетом эллипса. < 1. |
|
а |
|||
|
|
Эксцентриситет характеризует форму эллипса: чем меньше эксцентриситет, тем меньше его малая полуось в отличается от большой полуоси а, то есть тем меньше вытянут эллипс вдоль фокальной оси
а 2 |
с 2 |
в 2 |
|
|
в |
2 |
|
1 |
|
с |
2 |
1 |
2 . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
а |
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 14. Эллипс, симметричный относительно осей координат, |
||||||||||||||||||||||||||||||||
проходит через точки |
|
|
|
|
|
|
|
|
|
и А 6; 0 . Написать его уравнение, |
|||||||||||||||||||||||
М 2 |
3 ; |
|
6 |
|
|||||||||||||||||||||||||||||
найти эксцентриситет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Решение. Координаты точек М и А должны удовлетворять уравне- |
||||||||||||||||||||||||||||||||
|
|
|
|
12 |
|
|
6 |
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нию (2.22): |
|
а 2 |
в 2 |
Решив систему, получим а 2 |
36 , в2 |
9, то- |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
36 |
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х 2 |
у 2 |
в2 |
а 2 с2 |
с2 |
|||||||||
гда |
уравнение |
|
|
эллипса |
|
|
|
|
|
|
|
|
|
|
|
1; |
|||||||||||||||||
|
|
|
|
|
|
36 |
|
|
|
9 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
а 2 |
в2 |
|
36 9 27 ; |
|
с |
|
|
|
|
27 3 3 |
|
|
3 |
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
36 |
|
|
6 |
|
|
2 |
|
|
|
|
|
|||||||
Гипербола
Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Обозначим фокусы F1, F2, расстояние между ними – 2с, постоянную из определения – 2а (по условию 2а < 2с, а < с). Выберем систему координат так же, как при выводе уравнения эллипса (см. рис. 28).
По определению |
М F |
М F |
2а , или МF |
МF |
2а ; |
|||||||
|
|
|
1 |
2 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
с 2 |
у 2 |
|
х с 2 |
у 2 |
2а ; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
с 2 |
у 2 |
|
2а |
х с 2 |
у 2 ; |
|
|||
62
