Курс лекций по высшей математике. 2 часть

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Владивостокский государственный университет экономики и сервиса

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Составим ряд из абсолютных величин членов данного ряда:

.pdf

Скачиваний:

Добавлен:

13.04.2015

Размер:

4.24 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Замечание:

Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходится.

Например, ряд	1 n	сходится по признаку Лейбница, а ряд		1	–
	n		n 1 n
n 1

расходится (гармонический ряд)

5. Остаток ряда и его оценка

Рассмотрим сходящийся ряд

U1 U2 ...	Un	Un 1 Un 2 ...		(1)
Вычисление суммы ряда	S	lim Sn	обычно	технически очень
		n
сложно. Поэтому в качестве S берут Sn:S			Sn. Точность последнего ра-
венства возрастает с увеличением n.

Определение: Если числовой ряд сходится, то разность Rn=S–Sn называется n–м остатком ряда.

Таким образом, Rn представляет собой сходящийся числовой ряд:

Rn=Un+1+Un+2+…

Заметим, что lim Rn	lim S Sn S S 0 .
n	n

Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна |Rn|=|S–Sn|.

Таким образом, если требуется найти сумму ряда с точностью до >0, то надо взять сумму такого числа n первых членов ряда, чтобы вы-

полнялось условие: |Rn|< .

Однако в общем случает находить точно Rn не удается.

Теорема: (об оценке остатка знакочередующегося числового ряда) Если знакочередующийся числовой ряд сходится по признаку

Лейбница, то его n–й остаток по абсолютной величине не превосходит модуля (n+1)–го члена ряда.

Доказательство: Пусть ряд U	U	2	U	3	U	4	...	1 n	U	n	... схо-
1
дится по признаку Лейбница. Тогда			n–й		остаток			ряда	Rn= (Un+1–

Un+2+Un+3–…) сам является суммой знакочередующегося числового ряда

и по теореме Лейбница |Rn|

|Un+1|. Теорема доказана.

Пример:

Вычислить

с точностью

до

0,01

сумму ряда

....

1! 3!

Очевидно,

ряд

сходится

по

признаку

Лейбница.

0,166;

0,008 0,01 . Поэтому S 1–0,166

0,84.

§2. Функциональные ряды

1. Основные понятия

Определение. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают:

u1 x	u2 x	... un x ...	(1)
Определение. Если при x	x0	ряд (1) сходится, то	x0 называется
точкой сходимости ряда (1).

Определение. Множество всех значений x , при которых функциональный ряд сходится, называется областью сходимости этого ряда.

Очевидно, что в области сходимости функционального ряда его сумма является функцией от x . Будем ее обозначать S(x) .

2. Степенные ряды

Определение. Степенным рядом называется функциональный ряд вида:

a 2 ...

a n ...

(2)

где a, a0 , a1, a2 , ..., an , ... – некоторые числа, называемые коэффициен-

тами степенного ряда.

Теорема (о структуре области сходимости степенного ряда).

Областью сходимости степенного ряда:

a a

a 2 ...

a n ...

(2)

является интервал

a R;a

R ,

к которому в зависимости от конкрет-

ных

случаев

могут

быть

присоединены

точки

R и

a R , где

lim

(если этот предел существует). В каждой точке интервала

an 1

R;a R

ряд сходится абсолютно.

Доказательство. Рассмотрим ряд, составленный из абсолютных ве-

личин членов данного ряда:

2 ...

n ...

(3)

Применим к ряду (3) признак Даламбера.

lim

un 1

lim

an 1

x a

n 1

x a

lim

an 1

x a

Возможны три случая.

1.Если	x	a	1	или	x a	R , или x a R; a R , то ряд (3)

		R

сходится. Но тогда по достаточному признаку сходимости знакопеременного ряда сходится и ряд (2), причем абсолютно.

2.Если	x a	1 , то ряд (3) расходится.
	R

В этом случае

lim

, то есть при достаточно больших n

un 1

, значит

lim

0 и

lim un 0 , следовательно, ряд (2) рас-

ходится по следствию из необходимого признака сходимости. Теорема доказана.

Определение. Интервал a R;a R называется интервалом сходимости степенного ряда, а половина его длины R называется радиу-

сом сходимости степенного ряда.
Замечание. Всякий степенной ряд (2) сходится при	x	a .	Если
других точек сходимости у ряда (2) нет, то считают, что	R	0 .	Если

степенной ряд сходится во всех точках числовой прямой, то считают, что R .

Примеры. Найти область сходимости степенного ряда.

1.xn

n 1 n

n 1

и применим к

нему

признак

Даламбера:

un 1

n 1

lim

1 или

Ряд сходится, если

(

1;1) –это и есть интервал схо-

димости. Исследуем концы этого интервала. При

x 1 получаем знако-

положительный числовой ряд

. Этот ряд расходится как обоб-

щенный гармонический ряд с

. При

получаем знакочере-

1 n

дующийся числовой ряд

. Применим к нему признак Лейбни-

n 1

ца.

> ,

n 1

2) lim

lim

0 , следовательно ряд сходится. Областью схо-

1;1 ; R

1 .

димости данного ряда является промежуток

n! x

5 .

n 1

Составим

ряд

из абсолютных

величин

членов

данного

ряда

n ,

и применим к нему признак Даламбера.

n 1

un 1

n 1 !

x a

n 1 ,

n 1 !

x a

n 1

0, x a

lim

lim n

, следователь-

, x

но, областью сходимости данного ряда

является одна

точка

a ;

0 .

3. n

Составим ряд из абсолютных величин членов данного ряда

и применим к

нему

признак

Даламбера.

1 !

lim

при всех x

, следовательно,

n 1

n 1 !

;

областью

сходимости

данного

ряда

является

промежуток

;

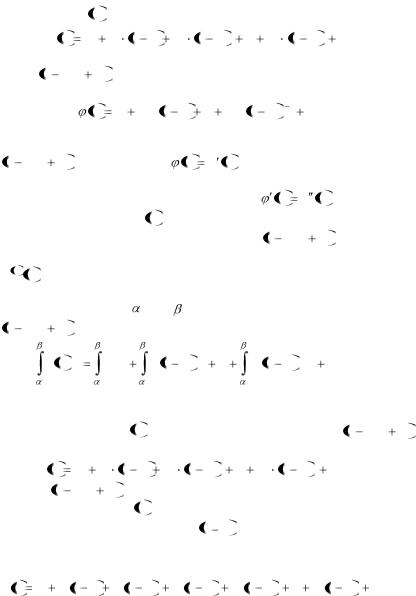
3. Свойства степенных рядов

Отметим здесь, без доказательства, три важных свойства степенных рядов.

1.Сумма S x

степенного ряда

S x

x a

a 2 ...

a n

...

(2)

является непрерывной функцией в каждой точке интервала сходи-

мости a

R;a

R .

2.Ряд

a ...

a n 1

... ,

(4)

полученный почленным дифференцированием ряда (2), является

степенным рядом с тем же,

что

и ряд (2), интервалом сходимости

R;a

R . Сумма ряда (4)

x .

Замечание. Ряд (4) также можно почленно дифференцировать и

сумма полученного после этого ряда равна

S x ,

и так далее.

Таким образом, сумма S x

ряда (2) является бесконечно дифференци-

руемой функцией в интервале сходимости

R;a

R .

Сумма ряда

полученного из

ряда

(2)

n –

кратным

дифференцированием,

равна

S n

x . Область сходимости степенного ряда при дифференцировании

не изменится.

3. Пусть

числа

принадлежат интервалу

сходимости

R;a

R ряда (2). Тогда имеет место равенство

S x dx

a dx

...

a n dx ...

(5)

4. Разложение функций в степенные ряды

Пусть функция

x бесконечно дифференцируема в

R;a

и является суммой степенного ряда:

a 2 ...

x a n ...

(1)

где

R;a

R –интервал сходимости ряда (1). В этом случае го-

ворят,

что функция

x разлагается в степенной ряд в окрестности

точки

или

по

степеням

a .

Определим

коэффициенты

a0 , a1, a2 , ..., an , ... этого ряда, для чего продифференцируем n

раз ряд

(1).

f x

x a

a 2

a 3

x a 4

... a

a n

...

(1)

a 2

3 ...

a n 1 ...

2 3a

3 4a

a 2

...

a n

2 ...

2 3a

2 3 4a x

a ...

na x

a n

3 ...

… …

… … …

… … … …

f ( n ) x

2 3 ... n

nan ...

… … … … … … … … …

Все ряды имеют интервалы сходимости

R;a

R . При x

a из

полученных тождеств

получаем:

a0 ,

f a

a1 ,

2a2 ,

2 3a

, …,

f ( n ) a

2 3 ... n

1 n

, … Отсюда находим

коэффициенты степенного ряда (1):

a ,

f a

, …, a

, … Подставляем полученные значения ко-

эффициентов в ряд (1), получаем

a 2

...

n a

a n

...

(2)

Ряд (2) называется рядом Тейлора для функции f

в точке a . В

частном случае при a

0 ряд (2) принимает вид:

f 0

...

f n 0

(3)

и называется рядом Маклорена.

Таким образом, если функция

f x

является суммой степенного

ряда, то этот ряд называется рядом Тейлора для функции

x .

Пусть теперь дана бесконечно дифференцируемая в точке a

функ-

ция

x .

Составим

для

нее

формально

ряд

Тейлора:

a ...

... .

Совпадает ли сумма полученного ряда Тейлора с функцией f x ,

для которой он составлен? Оказывается, не всегда. При каких условиях сумма ряда Тейлора совпадает с функцией, для которой он составлен?

Рассмотрим n –ю частичную сумму ряда Тейлора:

Sn x f a	f a	x a	...	f n a	x a n	(4)
	1!			n!

Многочлен (4) называется многочленом Тейлора степени n. Раз-

ность Rn x

x называется остаточным членом ряда Тейлора.

Теорема.

Для того, чтобы бесконечно дифференцируемая в точке a функция

f x

являлась суммой составленного для нее ряда Тейлора, необходимо

и достаточно, чтобы lim Rn x

0 .

Можно показать, что остаточный член можно представить в форме

Лагранжа:

x a

, где

c –некоторое

число из

интервала

1 !

a; x

. Таким образом

f x

f a

a ...

f n a

x a

f n 1 c

n 1

(5)

1 !

Формула (5) называется формулой Тейлора, а ее частный случай

при a

0 называется формулой Маклорена:

f 0

x ...

f n 0

f n

1 c

xn 1 , где

0; x .

1 !

5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена

1.Разложение функции

в ряд Маклорена.

x ...

...

ex .

0 ...

...

e0 1 .

Составим для функции

формально ряд Маклорена:

x 2

...

x n

... .

Найдем

область

сходимости

этого

ряда

lim

1 n!

lim

0 при любых x,

( n 1)!

следовательно,

областью сходимости ряда является промежуток

;

. Заметим, что так как ряд сходится абсолютно, то lim

при любых x и тем более

lim

0 при любых x.

n 1

ex ,

n 1

eс ,

тогда

lim R

lim

xn 1

0. Таким образом, имеет место раз-

1 !

ложение при x

;

...

(1)

2. Разложение функции

sin x

в ряд Маклорена.

Вычислим производные данной функции.

cos x

sin x

( x)

Sinx

Sin ( x

)

( x)

Cosx

Sin ( x

)

f (4) ( x)

Sinx

Sin ( x

)

… … … …

f (n) ( x)

Sin ( x

)

… … … …

Значение

f (x)

производных

точке

f 0

0 , f 0 1,

f 0

0 ,

1, f (4) (0)

0 , …,

f (2n 1) (0)

(

1)n 1 ,

f (2n) (0) 0 .

Исследуем

остаточный

член

ряда.

1 (c)

x n 1

Rn ( x)

(n 1)!

Sin(c

)

1 .

lim

n 1

1 !

lim Rn

0 .

Sin c	n 1				x	n	1
		2	x n 1					, так как
		2


n	1 !			(n			1)!

0 ,	следовательно,	lim	Rn x	0 и
		n

Рекомендуем показать самостоятельно, что областью сходимости ряда является помежуток ( ; ) . Таким образом имеет место разло-

жение при x ( ; ) :

100

x 3

( 1)n 1

x 2n 1

Sinx

...

(2n

1)!

3. Разложение функции

f (x)

Cosx ряд Маклорена.

Дифференцируя ряд (2) получаем разложение при x (

;

) :

x 2

x 4

( 1)n 1

x 2n 2

Cosx

...

(2n

2)!

4. Биномиальный ряд.

Разложим в ряд Маклорена функцию f

x (1 x)m ,

где

любое действительное число. Для этого вычислим производные.

(2)

(3)

0 –

f ( x)

m (1 x)m 1 ,

f ( x) m (m 1) (1 x)m 2 ,

f ( x) m (m 1) (m 2) (1 x)m 3 ,

… … … … …

f (n) ( x)

m (m 1) (m 2)

... (m

x)m

n ,

… … … … … … .

При

получаем:

f 0

m ,

m (m

1) ,

m (m

2) ,…, f (n)

m (m

...

n 1

,….

Можно показать, что областью сходимости ряда является промежу-

ток

1;1 (на концах интервала ряд сходится или расходится в зависи-

мости от конкретного значения m ) и что

lim Rn

0 . Таким образом,

при x

1;1

имеет место разложение

x m

x 2

m 2

x3 ...

(4)

m 1

2 ....

x n ...

Ряд (4) называется биномиальным рядом.

5. Разложение функции

f (x)

lnx

в ряд Тейлора.

При

функция

f (x)

lnx не определена,

поэтому ее нельзя

разложить в ряд Маклорена. Разложим ее в ряд Тейлора, например, по степеням (x 1) . Для этого вычислим приводные.

f x	1		x	1 ,	f x	1 x 2	1! x 2 ,	f ( x) 1 2 x 3 2! x 3 ,

		x

f (4) ( x)	1 2 3			x 4	3! x	4 , …, f n	x (	1)n 1 (n 1)! x n , ….

101

При

x 1

получаем:

f (1)

0 ,

f (1) 1 , f

(1)

1! , f (1)

2! ,

f (4) (1)

3! , …, f n

1 (

1)n 1

1)! , ….

Можно показать, что областью сходимости ряда является промежу-

ток 0;2

и что

lim Rn

0 . Таким образом, при x

0;2 имеет место

разложение:

x 1 x 1 2

x 1 3

1 n 1

x 1 n

ln(x)

...

... .

(5)

Замечание. Разложение функций в ряды Тейлора или Маклорена непосредственно часто связано с громоздкими вычислениями при нахождении производных и исследовании остаточного члена. На примерах покажем некоторые приемы, позволяющие избежать этих трудностей.

Пример 1. Разложить в степенной ряд функцию e x2 .

формуле

(1)

сделаем замену

переменной:

t 2 ,

получим

e t

(

...

... при t

;

Переобозначим t

на x , получим нужное разложение:

(

...

Пример 2. Разложить в степенной ряд функцию

f ( x)

x 2

Очевидно, f ( x)

x 2 ) 1 .

Обозначим

x 2

и воспользуемся

биномиальным рядом при m

1 .

1 2

...

(

1)n

1 2 ... n

...

t) 1

t 2

t 3

...

(

1)n t n

... ,

1;1 .

(6)

Возвращаясь к переменной x , получаем при x

1;1 :

x 2

x 4

x 6

...

(

1)n

x 2n ...

(7)

x 2

Пример 3. Разложить в степенной ряд функцию f (x)

ln(1

x) .

Проинтегрируем обе части разложения (6) от 0 до x при x

1;1 :

x dt

1 t

t 2

t 3

...

1 n

t n

... dt

или

0 1 t

ln(1

...

( 1)n

x n

...

(8)

102

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.04.2015116.32 Кб13кречмер.docx
#
15.03.2016121.86 Кб24КСЕ Тезаурус 2009 г..doc
#
15.03.2016614.4 Кб92КСЕ. Конспект лекций.Часть_1.doc
#
15.03.2016334.85 Кб29КСЕ. Конспект лекций.Часть_2.doc
#
13.04.20153.69 Mб161Курс лекций по высшей математике. 1 часть.pdf
#
13.04.20154.24 Mб61Курс лекций по высшей математике. 2 часть.pdf
#
13.09.2019254.49 Кб12Курсач.rtf
#
17.09.20192.13 Mб18КУРСОВАЯ ВАСИЛЬЕВА.doc
#
13.04.201576.55 Кб82курсовая живопись Ямаева.docx
#
13.04.201538.08 Кб74Курсовая Чекова фирменный стиль.docx
#
18.08.201968.1 Кб21Лабораторная работа 7.doc