§2 Теорема Чебышева
п
.1.Теорема
Чебышева
Е
сли
-
попарно независимые случайные величины,
дисперсии которых ограничены числом
с,
то как бы мало ни было положительное
число
,
выполняется неравенство
В
условиях теоремы
Теорема
утверждает, что при рассмотрении большого
числа независимых случайных величин,
имеющих ограниченные дисперсии, почти
достоверно, что отклонение среднего
арифметического случайных величин от
среднего арифметического их математических
ожиданий будет по абсолютной величине
сколь угодно малым.
Обозначим
.
Найдем математическое ожидание
(Свойства: м.о. суммы равно сумме м.о.
слагаемых, постоянный множитель можно
выносить за знак м.о.) :
=
=
.
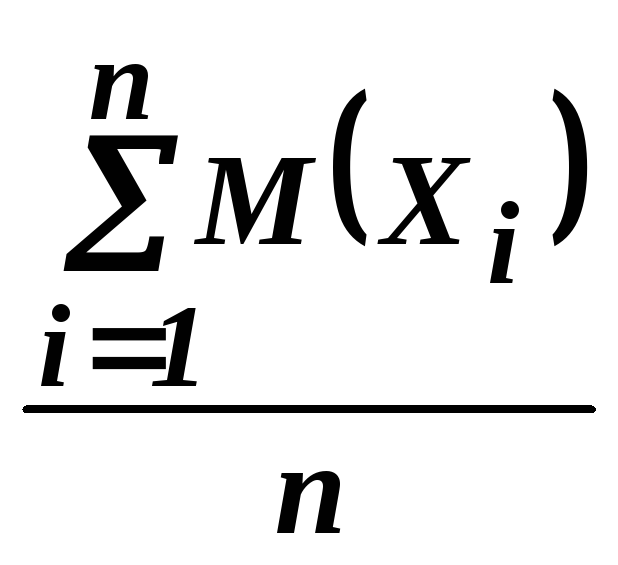Применим к
неравенство
Чебышева:
(1).
Найдем
дисперсию
,
применив свойства: дисперсия суммы
равна сумме дисперсий слагаемых,
постоянный множитель можно выносить
за знак дисперсии, возведя его в квадрат)
:
=
=
.
По условию дисперсии всех случайных
величин ограничены константой с,
поэтому
=
.
Итак,
.
Подставим в (1):
.
Перейдем
к пределу при
и получим искомое равенство.
|
№ |
Условие |
D(X) (c) |
|
n |
|
|
1 |
Дисперсия каждой из 1000 независимых случайных величин равна 4. Определить вероятность того, что отклонение средней арифметической этих величин от средней арифметической их математических ожиданий по модулю не превзойдет 0,1. |
|
0,1 |
|
Р
>
|
|
2
|
Для определения средней урожайности поля площадью 1800га взяли выборку по 1кв.м. с каждого гектара. Известно, что по каждому гектару поля дисперсия не превышает 6. Оценить вероятность того, что отклонение средней выборочной урожайности отличается от средней урожайности по всему полю не более чем на 0,25ц. |
|
|
|
|
Если
все случайные величины имеют одно и то
же математическое ожидание а,
то имеет место неравенство:
|
|
Условие |
D(X) (c) |
|
n |
|
|
1 |
Сколько должно быть проведено независимых измерений некоторой величины, чтобы с вероятностью, не меньшей чем 0,98, можно было утверждать, что среднее арифметическое результатов измерений отличается от истинного значения по модулю меньше чем на 0,01, если дисперсия отдельного результата измерения не превосходит 1?
|
|
|
|
|
|
2 |
Определить, сколько надо произвести замеров поперечного сечения деревьев на большом участке, чтобы средний диаметр деревьев отличался от истинного значения а не более чем на 2 см с вероятностью не меньшей 0,95. Среднее квадратическое отклонение поперечного сечения деревьев не превышает 10 см и измерения проводятся без погрешности. |
|
|
|
|
|
3 |
Сколько должно быть проведено измерений, чтобы с вероятностью, не меньшей чем 0,9973, можно было утверждать, что среднее арифметическое результатов измерений отличается от истинного значения по модулю меньше чем на 0,01, если среднее квадратическое отклонение отдельного результата измерения не превосходит 0,03?
|
|
|
|
|
