4.9 Методы анализа нелинейных цепей

Анализ нелинейных электрических цепей осуществляется также как и линейных цепей на основе уравнений Кирхгофа. Но, так как нагрузки зависят от электрических параметров, в нелинейных цепях постоянного тока составляемые алгебраические уравнения содержат изменяющиеся коэффициенты. Решение таких уравнений связано с определенными трудностями. В нелинейных электрических цепях переменного тока решаемые нелинейные дифференциальные уравнения также содержат переменные коэффициенты, что тоже затрудняет их решение. Поэтому методы решения задачи анализа в нелинейных цепях разделяют на две части: приближенные (предварительные) и точные (окончательные).

К приближенным методам относятся, например, методы, основанные на линеаризации, т. е. на замене нелинейных характеристик линейными (метод кусочно-линейной аппроксимации, метод аналитической апроксимации).

К точным относятся методы, в которых нелинейные характеристики описываются точно, например, с помощью аналитических выражений (формул). Наибольшее распространение получили: аналоговые методы математического моделирования и цифровые методы (методы Эйлера и Рунге-Кутта).

На простых примерах рассмотрим эти методы.

Метод кусочно-линейной аппроксимации

Пусть дана цепь (рис. 4.28), содержащая нелинейную индуктивность и линейное сопротивление. Цепь питается переменным напряжениемu(t)=U_msint. Вебер амперная характеристика(ВбАХ) задана графиком (рис.4.29). Аппроксимируем характеристику тремя отрезками (1-2), (2-3) и (4-1). Цепь стала кусочно линейной. Если поток не превышает m, то в цепи не возникает ток. Появление в цепи тока приводит к постоянству магнитного потока. Расчет начнем с момента времениt=0. Пусть в этот момент рабочая точка характеристики находилась на отрезке (1-2) и потокосцепление равно:. По второму закону Кирхгофа составим уравнение процесса:u = ir +. Учтем, что пока поток не достиг максимального значения, в цепи нет тока:u = .Найдем магнитный поток: .

Это решение справедливо пока m. Найдем постоянную интегрирования (с) в момент времениt=0:(0)= -_m=. Отсюда:c= .

Определим момент времени t1 когда=+m. Для этого подставим в формулу потока этот момент времени:_m= -, откуда:

cos t1=или . Приt>t1 рабочая точка перешла на участок (2-3) (рис.4.29). Потокосцепление равно:= +mи поэтому его производная равна нулю: . Тогда основное уравнение примет вид: . Ток равен: .

Э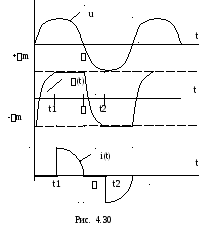то решение будет справедливо до тех пор, пока ток не станет равным нулю. Этот момент времени равен (t=). Ток на участке 2-1 равен нулюi=0. Потокосцепление можно определить аналогично: . Постоянную интегрирования с1 найдем при (t=): . Отсюда:c1=_m-. Найдем момент времениt2, когда потокосцепление равно: , отсюда: .

При t>t2 уравнение для тока такое же как при t>t1: . Результаты расчетов проиллюстрируем временными графиками (рис.4.30)

Рассмотрим другой пример. Пусть аппроксимация имеет вид (рис.4.31). Порядок расчета оставим без изменений. Расчет начнем с момента времени t=0. Рабочая точка находится на участке 1-2 (точка 1), которая характеризуется двумя параметрами:Процессы в заданной электрической схеме описываются уравнением:u=ir+. Учитывая, что на участке 1-2 индуктивность линейна, уравнение примет вид: , где . Это уравнение линейно и его решение имеет вид:i(t)=Ae^pt+i_n=. Постоянную интегрирования А найдем приt=0: -i1=. Тогда: . Полученное решение будет справедливо до тех пор, пока ток . Найдем момент времени, когда ток : . Полученное уравнение является трансцендентным, поэтому поискt1 осуществляют графически.

Приt>t1 рабочая точка переходит на участок (2-3), на котором ток равен:

. Когда этот ток вновь станет равным i1, рабочая точка перейдет на участок (2-1). Найдем этот момент времениt2: . Отсюда: . Дальнейшие расчеты повторяются. Результаты расчетов представлены на (рис.4.32).

Сравнивая результаты расчетов, убеждаемся в их различии.

Метод математической аппроксимации

Для нелинейной характеристики (рис.4.33) подберем аналитическое выражение. Пусть это будет гиперболическая функция (гиперболический синус): . Найдемиметодом выбранных точек. На характеристике выберем две точки и их координаты подставим в исходную формулу: Поделим первое выражение на второе:. Изменяя коэффициент, строим функциюна графике (рис.4.34). Точка пересечения этого графика с линиейkдает величину. Коэффициентнайдем по формуле: 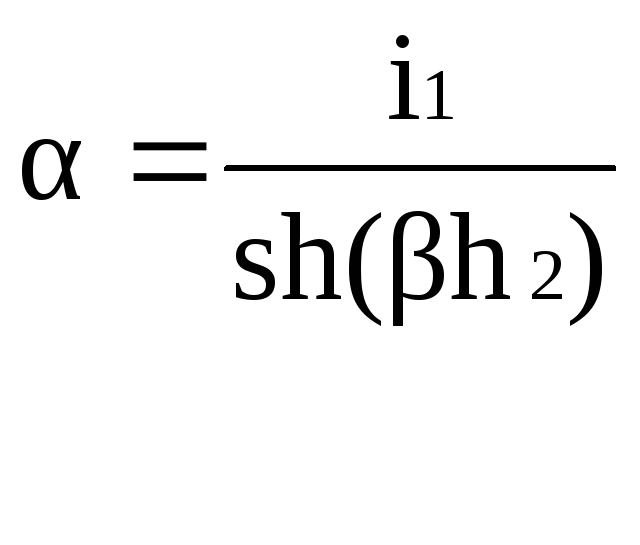. Таким образом, получили нелинейную зависимость в виде формулы:.

Рассмотрим другой вариант подбора аналитического выражения, например, в виде степенного ряда: . Коэффициентыaиbтакже найдем методом выбранных точек. Получим следующую систему уравнений:_.Решим эту систему относительно коэффициентов: 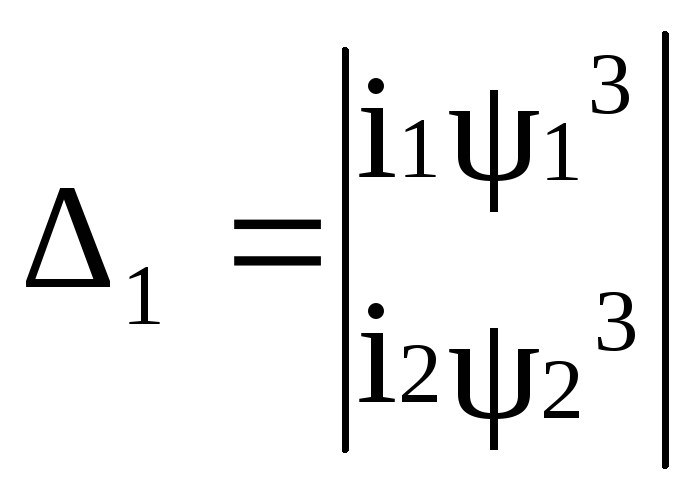_;;. Тогда коэффициенты равны: ; .

Метод Эйлера

Решим задачу (рис.4.28) на основе математической аппроксимации. Основное уравнение процессов: примет вид: . Последнее уравнение является нелинейным дифференциальным уравнением первого порядка. Решим его, например, методом Эйлера. Рассмотрим алгоритм решения методом Эйлера:

. Приведем это уравнение к конечным разностям:

. Тогда решение для (k+1) шага будет иметь вид:

Из нелинейной функции найдем потокосцепление: илии подставим его в дифференциальное уравнение или . Приведем это уравнение к форме Коши . Тогда решение будет иметь вид: .

Более точное решение можно получить методом Рунга-Кутта. Здесь этот метод рассматривать не будем.