ВОПРОСЫ ГОСУДАРСТВЕННОГО ЭКЗАМЕНА

91

К оглавлению ↑

степеней могут выражаться один через др. (рассмотрим , тогда, т.к. x4+4=(x2-2x+2)*(x2+2x+2),

то получаем ); 2.- вложенные радикалы (н-р, , ). Две проблемы

однозначности и соотношение между радикалами (н-р, 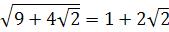); 3.- общие алгебраич. выраж-я (н-р, алгебраич. число γ, определенное ур-ем γ5+γ+1=0). Требуется, чтобы полиномы, определяющие алгебраич. числа и ф-ции, были неприводимыми (неразложимыми).

Представление трансцендентных ф-ций.

Трансценд. ф-ции группируются в неск-ко классов ф-ций, каждый из кот. имеет свои правила преобраз-я и упрощения. Классы: 1.- кл. тригонометрич. ф-ций; 2.- кл. экспоненц. ф-ций; 3.- кл. логарифм. ф-ций; 4.- кл. обратных тригонометрич. ф-ций. Трансцед. ф-ции могут явл-ся аргументами и коэфф-ми рацион. ф-ций, а также входить в алгебраич. ф-ции.

Представление матриц.

Матрица имеет вид , где aij-некот. аналитич. выраж-я, i=1,…, n; j=1,…,m. Или A=(aij)n,m. Если n и m – заданные явно натур. числа, то и запись матрицы м.б. конкретной. Если в записи матрицы присутствует только правая часть, то такое представление наз-ся явным. Если запись матриц осуществлена в односимвольном виде, т.е. левой частью (А), то такое представление наз-ся неявным. Плотные матрицы. Это матрицы с большим кол-вом ненулевых элтов. Представляются в виде прямоугольной табл. или массива. Алгоритм Барейса. Барейс предложил семейство методов исключения без использования дробей, т.е. таких, где все необходимые деления выполняются точно. Разреженные матрицы. Методы запоминания разреженных матриц с символьными эл-тами аналогичны методам запоминания различных полиномов; можно использовать списки вида {(aij,i,j)}, где aij-знач-е эл-та (аналит. выраж-е), i,j-номер строки и столбца, указывающие положение этого эл-та в матрице.

Представление рядов.

Ряды Тейлора. Необходимо предусмотреть алгоритмы «отбрасывания высших степеней». Для операций +,-,*,/ (C=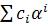; B=; A=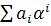): C=A+B, ; C=A-B, ;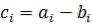

C=A*B, 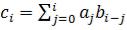; , . Ряды Фурье. Имеют вид

.

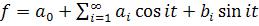Эффективность алгоритмов.

Литература: [1], [2].

2. Алгоритм Евклида

Вычисление НОД.

Число а называется общим делителем чисел b1, b2,…, bn, если оно является делителем каждого из чисел b1, b2,…, bn.

92

К оглавлению ↑

Наибольшим общим делителем целых чисел a1,…,an , называется такой их общий делитель, который делится на любой общий делитель этих чисел: обозначается НОД (a1,…,an).

и b, то d=НОД(a,b), где d=

Простой способ a= 24 b=6 24-6=18 18-6=12 12-6=6 < НОД

6-6=0

Теорема Евклида.

Теорема Евклида

Пусть a и b – два целых числа, b ≠ 0 и a = bq + r (0 ≤ r < |b|). Тогда НОД (a,b) = НОД (b,r).

Алгоритм Евклида, сравнение алгоритмов.

Для нахождения НОД двух целых чисел применяется способ «последовательного деления», называемый алгоритмом Евклида.

Сущность алгоритма Евклида состоит в том, что в силу теоремы Евклида задача нахождения НОД (a,b) сводится к более простой задаче нахождения НОД (b,r), 0 ≤ r < |b|. Если r = 0, то НОД (a,b) = b. Если же r ≠ 0, то получаем цепочку неравенств

a= bq0 + r1, 0 ≤ r < |b|,

b= r1q1 + r2, 0 ≤ r2 < r1,

……………………

rn-2 – rn-1qn-1 + rn, 0≤ rn < rn-1, rn-1 = rnqn + rn+1.

Приходим к выводу: если к целым числам a,b, где b ≠ 0, применить алгоритм Евклида, то последний ненулевой остаток в этом алгоритме и есть НОД (a,b).

Пример: a=86, b=32

a = b*q + p1 86 = 32*2 + 22

32 = 22*1 + 10

22 = 10*2 +2

10 = 2*5 + 0

Ответ: НОД (86, 32) = 2

Сравнение алгоритмов

Сравним «простой» алгоритм и алгоритм Евклида. Для малых чисел ни один из них не дает преимущества в вычислениях, но для больших параметров эффективней применять алгоритм Евклида.

Соотношение Безу.

(Целые числа называют взаимно простыми, если любой их общий делитель равен +1 или -1.) Теорема. Если целые числа a и b взаимно простые, то существуют целые числа u и v такие, что

au+bv=1.

93

К оглавлению ↑

Доказательство. Рассмотрим множество I = {ax + by | x,y ϵ Z}. a ϵ I, так как a = a*1 + b*0, и b ϵ I, так как b = a*0 + b*1. Обозначим через d наименьшее положительное натуральное число, принадлежащее множеству I. Так как d ϵ I, то, согласно определению множества I, существуют целые числа u и v такие, что au+bv=d; a, b ϵ I, значит, d – общий делитель чисел a, b. Но a, b – взаимно простые, d > 0, значит, d = 1 и au+bv = 1.

Пример. Пусть a = 5 и b = 7, тогда u = -4 и v = 3, т.е. 5*(-4) + 7*3 = 1.

Расширенный алгоритм Евклида.

Алгоритм, примененный к паре чисел a,b порождает последовательность такую, что

ri-1=riqi+ri+1 для 1≤i≤n, где r0=a, r1=b, rn+1=0.

Из этих формул легко получается рекуррентная последовательность:

из которой теперь следует классический результат rn=НОД(a,b)=una+vnb.

Литература: [1], [3], [5].

3. Модулярная арифметика

Модулярное исчисление состоит в осуществлении нескольких малых вычислений по модулям простых чисел и получении необходимого результата с помощью теоремы об остатках.

Китайская теореме об остатках.

Пусть n1 ,n2, …, nr - попарно взаимно простые числа. Пусть а1 ,а2, …, аr произвольно целые числа. Тогда система

имеет по крайней мере одно решение. Кроме того, если х' – другое решение этой системы, то

х х'(mod n1·n2· …·nr ).

Смешанная система счисления.

Идея, принадлежавшая Л.Гарнеру и представленная у Д.Кнута, состоит в том, чтобы связать с модулярным представлением еще одно представление, называемое смешанной системой счисления.

Основанием смешанной системы счисления называется множество из r 2 целых чисел n1,n2,…,nr, не обязательно взаимно простых. Если положим и n=n1·n2·…·nr, то имеется биекция (взаимно однозначное соответствие):

Обратное отображение определяется при помощи евклидовых делений: x=q1n1+z1, q1= q2n2+z2, … , qr-1= qrnr+zr.

94

К оглавлению ↑

В случае, когда все числа ni равны, получаем обычную позиционную систему счисления (смешанная система счисления, следовательно, это система, в которой основания варьируется).

Формулы определения цифр.

модулю ni.

Рассмотрим целое число x, модулярные компоненты которого x1,x2,…,xr тогда цифры x в системе со смешанным основанием ni обозначим через zi ; они находятся по формулам:

z1= x1mod n1,

z2= C2(x2-z1) mod n2,

z3= C3(x3-(N2z2+z2)) mod n3,

……………

zr= Cr(xr-(Nr-1zr-1+…+ N2z2+z1)) mod nr.

Чтобы осуществить обратный переход от системы со смешанным основанием к модулярному представлению, достаточно провести следующие вычисления:

x1=z1, x2=(z1+z2n1)mod n2,

x3=(z1+z2n1+z3n1n2)mod n3,

…

xr=(z1+z2n1+…+zrn1n2…nr-1)mod nr.

Сравнение чисел, определение цифр в позиционной системе счисления.

Пусть имеются два целых числа x и x', заданные своими модулярными компонентами, и мы хотели узнать, которое из этих чисел (можем считать, что они оба лежат в [0,m)) больше, по возможности не вычисляя явный вид этих чисел. Вычислим сначала цифры zi и zi', соответствующие x и x' в смешанной системе счисления, определяемой модулями. В этом случае x<x' тогда и только тогда, когда наибольший вес i, на котором различаются эти числа, таков, что

zi<zi'.

Определение цифр в позиционной системе счисления

Пусть целое х задано модулярными компонентами. Мы хотим вычислить его цифры в системе

соснованием b. По схеме Горнера

xmod b(…((zr mod)·nr-1+ zn-1 mod b)…)·n1+z1 mod b (x-(x mod b))/b

Так мы получили первую цифру x в системе счисления с основанием b.

Алгоритм умножения двух чисел?

Литература: [1], [4], [5].

4. Вычисление полиномов

Полином – многочлен.

Общая запись: y = anxn + an-1xn-1+…+a1x + a0

Вычисление х в степени n (бинарный метод, метод множителей, степенное дерево, аддитивная сложность).

Бинарный метод

Запишем n в двоичной системе счисления и заменим в этой записи каждую цифру “1” парой букв SX, а каждую цифру “0” – буквой S, после чего вычеркнем крайнюю левую пару букв SX. Результат, читаемый слева на право, превращается в правило вычисления хn, если букву “S” интерпретировать как операцию возведения в квадрат (S – square – квадрат), а букву “X ” – как операцию умножения на х.

95

К оглавлению ↑

Пример: n = 46, переводим в двоичную n = 1011102, заменяем SxSSxSxSxS, записываем правило: x2x4x5x10x11x22x23x46 итого 8 умножений

Метод множителей

Если n=p·q, где р – наименьший простой множитель числа n и q >1, то для вычисления хn мы можем сначала вычислить хр, а затем возвести это число в степень q. В случае, когда n простое, мы можем вычислить сначала число хn-1, а затем умножить его на х.

Если n=1, число хn имеется без всяких вычислений. Многократное применение этих правил дает нам процедуру вычисления хn для любого данного n.

Пример: n = pq ; p=7, q=13, n=91 y = x7 = ((x2)x)2x

y13 = (((y2)y)2)2y

итого 9 умножений

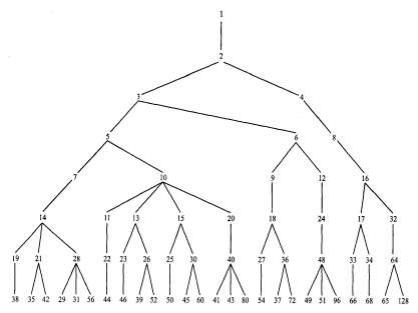
Степенное дерево

Допустим нужно вычислить xn. Находим на дереве число n, и тогда путь от корня дерева к узлу n определяет последовательность эффективного вычисления xn .

Аддитивная сложность

Аддитивной цепочкой для n называется всякая последовательность целых чисел 1=a0,…,ar=n, обладающих тем свойством, что ai=aj+ak при некоторых k ≤ j < i для всех i=1,2,…,r.

Заметим, что а1 всегда равно 2, а2 равно 2, 3 или 4.

Наименьшее значение r длины аддитивных цепочек для n обозначается через l(n) и называется

аддитивной сложностью или высотой числа n.

Схема Горнера.

f(x)=anxn+an-1xn-1+…+a1x+a0, an≠0 f(x)=(…(anx+an-1)x+…)x+a0

Весь процесс требует n умножений и n сложений.

Обобщенная схема Горнера.

Используется когда необходимо вычислить сразу как полином, так и его производную.

F’(x)=nanxn-1+(n -1)an-1xn-2+…+a1

Это удобно сделать, положив c0=an, b0=0

96

К оглавлению ↑

cj=cj-1x+an-j, bj=bj-1x+cj-1, 1≤j≤n.

Здесь cn=f(x) и bn=f’(x), вычисление требует (2n -1) умножений и (2n -1) сложений, причем нет

необходимости хранить в памяти новые коэффициенты j·aj.

Пример: f’(x)=2x7+0x6-3x5-4x4-x3-8

C0=a5=2

……

C5=C4*x+a0 = (((2x2-3)*x-4)*x-1)*x-8= f(x) b0=0

b1=b0*x+C0=2

……. b5=b4x+C4=2x4+3x2-4x-4

Литература: [1], [5].

5. Нахождение НОД полиномов от одной переменной

Наивный метод.

Пусть f и g полиномы и мы хотим вычислить их НОД. "наивный" метод (основан на алгоритме Евклида). Такие действия над полиномами с рациональными коэффициентами требуют неоднократного вычисления НОД целых чисел и что целые числа, фигурирующие в этих вычислениях, не всегда являются маленькими.

Модулярные методы.

Вычисления НОДа наивным методом наводят на мысль о модулярных методах, в которых нет возможности разбухания промежуточных выражений, поскольку целые числа по модулю 5 ограничены (четырьмя).

Вопросы: 1.- как вычислять нетривиальный НОД? 2.- что делать, если модулярный НОД не является модулярным образом НОД?м 3.- какова стоимость этого метода? Граница для коэффициентов НОД двух полиномов.

Неравенство Ландау-Миньотта, следствия.

98

К оглавлению ↑

ТЕОРИЯ ИНФОРМАЦИИ

1. Понятие информации формы её представления

Различные определения информации.

•Информация – это содержание сигналов, поступающих в кибернетическую систему из окружающей среды, которое может быть (раньше или позже) использовано системой для целей управления.

•Информация – не материя, а свойство организованной материи (нет такого свойства как масса, она не подчиняется законам сохранения массы и энергии). Сама информация не является материальной категорией.

Формы представления.

•Информация о каких-либо событиях и состоянии материальных объектов и, соответственно, сигналы, в которых содержится эта информация, могут быть представлены в непрерывной (аналоговой) и дискретной форме.

Канал связи.

Канал связи (channel, data line) — система технических средств и среда распространения сигналов для передачи сообщений (не только данных) от источника к получателю (и наоборот). Канал связи, понимаемый в узком смысле (тракт связи), представляет только физическую среду распространения сигналов, например, физическую линию связи.

Используют следующие характеристики канала

Эффективно передаваемая полоса частот ;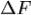

Динамический диапазон ;

Волновое сопротивление;

Пропускная способность;

Помехозащищённость ;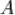

Объём .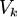

Помехозащищённость

Помехозащищённость . Где — минимальное отношение сигнал/шум;

Объём канала

Объём канала определяется по формул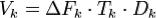е: , где — время, в течение которого канал занят передаваемым сигналом;

99

К оглавлению ↑

Для передачи сигнала по каналу без искажений объём канала должен быть больше либо равен объёму сигнала , т.е. 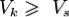. Простейший случай вписывания объёма сигнала в объём канала - это достижение выполнения неравенств , > и . Тем не менее, 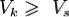может выполняться и в других случаях, что даёт возможность добиться требуемых характеристик канала изменением других параметров. Например, с уменьшением диапазона частот можно увеличить полосу пропускания.

Теорема Котельникова.

Теорема о выборках утверждает, что для точной дискретизации ее частота должна быть не менее чем в два разы выше наибольшей частоты гармоники, входящей в дискретизируемую величину [17]. Примером использования этой теоремы являются лазерные ком- пакт-диски, звуковая информация на которых хранится в цифровой форме.

Информация — нематериальная сущность, при помощи которой с любой точностью можно описывать реальные (материальные), виртуальные (возможные) и понятийные сущности. Информация — противоположность неопределенности. Канал связи — это среда передачи информации, которая характеризуется в первую очередь максимально возможной для нее скоростью передачи данных (емкостью канала связи).

Информация может быть двух видов: дискретная (цифровая) и непрерывная (аналоговая). Дискретная информация характеризуется последовательными точными значениями некоторой величины, а непрерывная — непрерывным процессом изменения некоторой величины. Непрерывную информацию может, например, выдавать датчик атмосферного давления или датчик скорости автомашины. Дискретную информацию можно получить от любого цифрового индикатора: электронных часов, счетчика магнитофона и т.п.

Литература: [1].

2. Энтропия

Основные подходы к измерению количества информации.

Понятие количества информации естественно возникает, например, в следующих типовых случаях:

1.Равенство вещественных переменных a = b, заключает в себе информацию о том, что a равно b. Про равенство a2 = b2 можно сказать, что оно несет меньшую информацию, чем первое, т.к. из первого следует второе, но не наоборот. Равенство a3 = b3 несет в себе информацию по объему такую же, как и первое;

2.Пусть происходят некоторые измерения с некоторой погрешностью. Тогда чем больше будет проведено измерений, тем больше информации об измеряемой сущности будет получено;

3.М.о. некоторой сл.в. содержит в себе информацию о самой сл.в. Для сл.в., распределенной по нормальному закону, с известной дисперсией знание м.о. дает полную информацию о сл.в.;

4.Рассмотрим схему передачи информации. Пусть передатчик описывается сл.в. X, тогда изза помех в канале связи на приемник будет приходить сл.в. Y = X +Z, где Z — это сл.в., описывающая помехи. В этой схеме можно говорить о количестве информации, содержащейся в сл.в. Y , относительно X. Чем ниже уровень помех (дисперсия Z мала), тем больше информации можно получить из Y . При отсутствии помех Y содержит в себе всю информацию об X.

В 1865 г. немецкий физик Рудольф Клаузиус ввел в статистическую физику понятие энтропии или меры уравновешенности системы. В 1921 г. основатель большей части математической

100

К оглавлению ↑

статистики, англичанин Роналд Фишер впервые ввел термин “информация” в математику, но полученные им формулы носят очень специальный характер.

В 1948 г. Клод Шеннон в своих работах по теории связи выписывает формулы для вычисления количества информация и энтропии. Термин энтропия используется Шенноном по совету патриарха компьютерной эры фон Неймана, отметившего, что полученные Шенноном для теории связи формулы для ее расчета совпали с соответствующими формулами статистической физики, а также то, что “точно никто не знает” что же такое энтропия.

Энтропия как мера степени неопределенности.

Энтропия - это мера степени неопределенности состоянии системы X (случайной величины) с конечным или счетным числом исходов.

Любое сообщение, с которым мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Например, на вход системы управления средствами противовоздушной обороны может быть передано сообщение о том, что в воздухе находятся две цели, летящие на определенной высоте, с определенной скоростью. Любое из этих сообщений описывает состояние какой-то физической системы.

Очевидно, если бы состояние физической системы было известно заранее, не было бы смысла передавать сообщение. Сообщение приобретает смысл только тогда, когда состояние системы заранее неизвестно, случайно.

Поэтому в качестве объекта, о котором передается информация, мы будем рассматривать некоторую физическую систему , которая случайным образом может оказаться в том или ином состоянии, т. е. систему, которой заведомо присуща какая-то степень неопределенности. Очевидно, сведения, полученные о системе, будут, вообще говоря, тем ценнее и содержательнее, чем больше была неопределенность системы до получения этих сведений («априори»). Возникает естественный вопрос: что значит «большая» или «меньшая» степень неопределенности и чем можно ее измерить?

Чтобы ответить на этот вопрос, сравним между собой две системы, каждой из которых присуща некоторая неопределенность.

В качестве первой системы возьмем монету, которая в результате бросания может оказаться в одном из двух состояний: 1) выпал герб и 2) выпала цифра. В качестве второй - игральную кость, у которой шесть возможных состояний: 1, 2, 3, 4, 5 и 6. Спрашивается, неопределенность какой системы больше? Очевидно, второй, так как у нее больше возможных состояний, в каждом из которых она может оказаться с одинаковой вероятностью.

Может показаться, что степень неопределенности определяется числом возможных состояний системы. Однако в общем случае это не так. Рассмотрим, например, техническое устройство, которое может быть в двух состояниях: 1) исправно и 2) отказало. Предположим, что до получения сведений (априори) вероятность исправной работы устройства 0,99, а вероятность отказа 0,01. Такая система обладает только очень малой степенью неопределенности: почти наверное можно предугадать, что устройство будет работать исправно. При бросании монеты тоже имеется два возможных состояния, но степень неопределенности гораздо больше. Мы видим, что степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностями состояний.

Перейдем к общему случаю. Рассмотрим некоторую систему 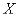, которая может принимать конечное множество состояний: 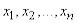с вероятностями 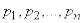, где

(18.2.1)

- вероятность того, что система 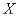примет состояние 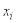(символом обозначается

событие: система находится в состоянии 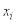). Очевидно, .

Запишем эти данные в виде таблицы, где в верхней строке перечислены возможные состояния системы, а в нижней - соответствующие вероятности: