
- •Часть 2. Случайные величины
- •§ 1. Понятие случайной величины
- •§ 2. Дискретная случайная величина
- •§ 3. Числовые характеристики дискретной случайной величины
- •1. Математическое ожидание
- •2. Дисперсия
- •3. Среднее квадратическое отклонение
- •4. Другие числовые характеристики
- •§ 4. Биномиальное распределение. Распределение Пуассона
- •§ 5. Одинаково распределенные независимые случайные величины
- •§ 6. Функция распределения
- •§ 7. Непрерывная случайная величина. Плотность ее распределения.
- •§ 8. Числовые характеристики непрерывной случайной величины
- •§ 9. Равномерное распределение
- •§ 10. Нормальное распределение
- •§ 11. Показательное (экпоненциальное) распределение
- •§ 12. Закон больших чисел
- •§ 13. Двумерные случайные величины
§ 5. Одинаково распределенные независимые случайные величины
Зададимся вопросом: почему для улучшения точности измерения некоторой величины делается несколько замеров и берется среднее арифметическое результатов?
Пусть
 − независимые одинаково распределенные
случайные величины. Тогда
− независимые одинаково распределенные
случайные величины. Тогда
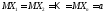 ;
;
 ;
;
 .
.
Рассмотрим
новую СВ
 .
Используя свойства математического
ожидания, дисперсии и среднего
квадратического отклонения, получим:
.
Используя свойства математического
ожидания, дисперсии и среднего
квадратического отклонения, получим:
 ;
;
 ;
;
 .
.
Следовательно,
при увеличении п
среднее значение (математическое
ожидание) СВ
 сохраняется, а рассеяние уменьшается,
т.е. улучшается точность измерения.
сохраняется, а рассеяние уменьшается,
т.е. улучшается точность измерения.
§ 6. Функция распределения
Определение. Функцией распределения случайной величины Х называется функция
 .
.
Т.е. функция распределения определяется вероятностью того, что СВ примет значение, меньшее аргумента этой функции.
Пусть
 и
и Рассмотрим события
Рассмотрим события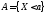 ,
, ,
,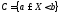 .
Очевидно, что
.
Очевидно, что и
и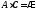 .
Следовательно,
.
Следовательно, .
Тогда
.
Тогда
 .
.
Таким
образом, функцией распределения
 СВХ
определяется
полностью.
СВХ
определяется
полностью.
Свойства функции распределения:
1)
 ;
;
2)
если
 ,
то
,
то ,
т.е. это неубывающая функция;
,
т.е. это неубывающая функция;
3)
 ;
;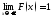 ;
;
4)
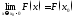 ,
т.е. функция непрерывна слева во всех
точках
,
т.е. функция непрерывна слева во всех
точках ;
;
5)
 .
.
Пример. 1) Составим функцию распределения для СВ Х, равной числу выпадений герба при двух бросаниях монеты.
 +
График.
+
График.
2)
Точка брошена на отрезок
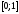 .
Случайная величинаХ
– ее абсцисса. Составим функцию
распределения этой СВ.
.
Случайная величинаХ
– ее абсцисса. Составим функцию
распределения этой СВ.
 +
График.
+
График.
§ 7. Непрерывная случайная величина. Плотность ее распределения.
Определение.
Случайная
величина Х
называется непрерывной,
если ее функция распределения непрерывна
всюду на R
и
дифференцируема во всех точках
 ,
за исключением, быть может, конечного
или счетного числа точек.
,
за исключением, быть может, конечного
или счетного числа точек.
Определение.
Функция
 называетсяплотностью
распределения
непрерывной случайной величины.
называетсяплотностью
распределения
непрерывной случайной величины.
Замечание.
Пусть
Х
– непрерывная СВ (НСВ). Найдем
 .
.
 ;
;
 ,
,
так
как функция
 непрерывна. Таким образом, для НСВ
непрерывна. Таким образом, для НСВ .
.
Следствие. Для непрерывной случайной величины
 .
.
Теорема 2. (О вероятности попадания значений НСВ в интервал)
Для
непрерывной случайной величины
 ,
где
,
где − плотность ее распределения.
− плотность ее распределения.
Доказательство.
 .
Ч.т.д.
.
Ч.т.д.
Следствие.
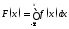 .
.
Свойства
плотности распределения
 :
:
1)
т.к. функция распределения
 является неубывающей, то ее производная
является неубывающей, то ее производная для всех
для всех ;
;
2)
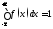 .
.
Вероятностный
смысл
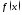 :
:
 .
.
Пример. 1) Найти плотность распределения СВ Х, заданной своей функцией распределения:

Решение.
 +
Графики.
+
Графики.
2)
Определить, при каком значении параметра
а
функция
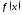 является плотностью распределения НСВ.
Найти
является плотностью распределения НСВ.
Найти .
.

Решение.
а)
Чтобы найти значение параметра а,
воспользуемся свойством плотности
распределения
 .
Получим:
.
Получим:
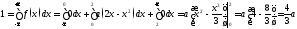 ;
;
 ;
;
 .
.
б)
 .
.
При

 .
.
При
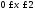
 .
.
При

 .
.
Следовательно,

в)
 .
.
§ 8. Числовые характеристики непрерывной случайной величины
Определение.
Математическим
ожиданием НСВ Х называется
число
 ,
где
,
где − плотность распределения СВХ.
(Предполагается, что этот интеграл
абсолютно сходится.)
− плотность распределения СВХ.
(Предполагается, что этот интеграл
абсолютно сходится.)
Если
 − функция НСВХ,
то
− функция НСВХ,
то
 .
.
Остальные характеристики НСВ вводятся аналогично характеристикам ДСВ.
Определение.
Дисперсией
НСВ Х называется
 .
.
Определение.
Средним квадратическим отклонением
НСВ Х называется
 .
.
Формула
для вычисления:
 .
.
Пример. НСВ Х задана своей плотностью распределения:
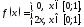
Найти

Решение.
1)

2)
 .
.
3)
 ;
;
 .
.
4)
 .
.
