5. Электроемкость. Конденсаторы.

ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА,

ЗАРЯЖЕННОГО КОНДЕНСАТОРА

Понятие электроемкости основано на существовании прямо пропорциональной зависимости между зарядом проводника q и его потенциалом  :

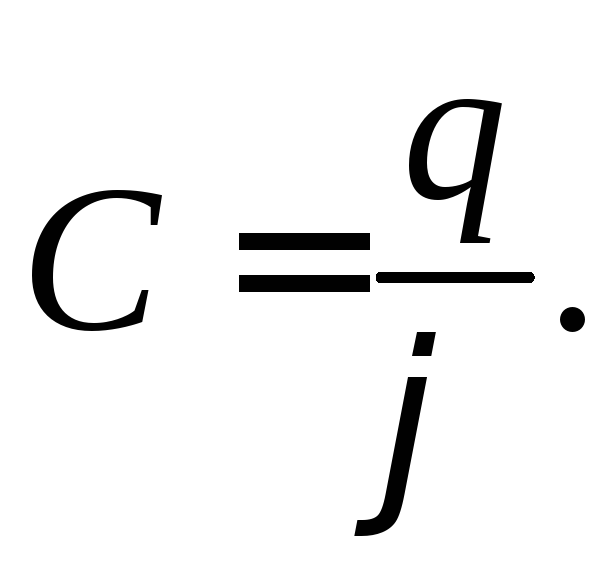(80)

Электроемкость проводника численно равна заряду, изменяющему его потенциал на единицу, она зависит от геометрических характеристик проводника: размеров, формы и диэлектрических свойств среды. Для шара электроемкость определяется через его радиус R и диэлектрическую проницаемость окружающей среды  :

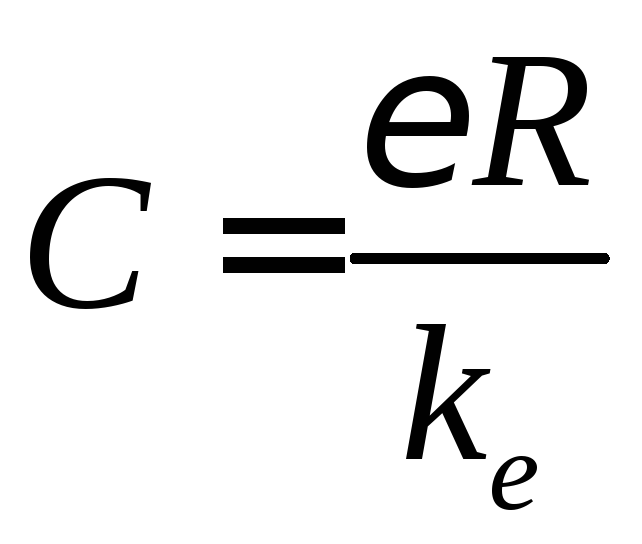. (81)

окружающие тела также влияют на электроемкость. Существуют устройства, например конденсаторы, электроемкость которых слабо зависит от окружающих тел. Электроемкость плоского конденсатора определяется площадью пластин S, расстоянием d между ними и диэлектрическими свойствами среды между пластинами:

(82)

При решении задач, в которых требуется найти заряд, потенциал и емкость заряженных проводников до и после их соединения, необходимо иметь в виду следующее:

1) при соединении проводников, имеющих разные потенциалы, заряды перераспределяются до тех пор, пока потенциалы проводников не станут одинаковыми, после этого вся поверхность проводников становится эквипотенциальной; соединение проводников тонкой проволокой предполагает, что зарядами, оставшимися на ней, можно пренебречь;

2) предполагается, что система проводников слабо взаимодействует с окружающими телами; суммарный заряд до и после соединения остается постоянным.

При решении задач, в которых рассматриваются конденсаторы, необходимо обратить внимание на следующее:

1) заряд на плоском конденсаторе, отключенном от источника питания, остается постоянным при изменении расстояния между пластинами или электрических свойств среды, заполняющей пространство между пластинами;

2) если конденсатор не отключается от источника, то при всех изменениях, указанных выше, конденсатор не является изолированной системой и заряд на нем меняется, но разность потенциалов между пластинами остается постоянной.

При решении задач, в которых определяется энергия плоского конденсатора, отключенного от источника, необходимо иметь в виду, что при изменении емкости заряженного конденсатора электрические силы совершают работу, равную убыли энергии конденсатора, в том случае, когда заряд на пластинах конденсатора не меняется. Если конденсатор не отключается от источника энергии, то работа совершается за счет убыли его потенциальной энергии.

В задачах, где требуется найти работу разряда при соединении двух заряженных проводников, следует использовать закон сохранения энергии. Работа разряда будет равна разности значений энергии проводников до и после соединения.

5.1. Примеры решения задач

Задача 11. Заряженный шар радиусом 3 см в вакууме приводится в соприкосновение с другим шаром радиусом 4 см, заряженным до потенциала 3000 В. После того как шары разъединили, энергия первого шара оказалась равной 2 мДж. Найти энергию шаров до соприкосновения, работу разряда, заряды первого шара до соприкосновения и второго шара после соприкосновения (рис. 11).

Дано: 2 = 3000 В Rl = 3 см = 0,03 м R2 = 4 см = 0,04 м = 2 мДж = 0,002 Дж  = 1

Найти: Wl, W2, A, q1, q'2.

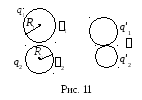
Решение. До соприкосновения оба шара были заряжены, причем

q₂ = ₂С₂; (83)

С₁ = ; (84)

С₂ = . (85)

При соприкосновении шаров заряды станут переходить с шара, имеющего больший потенциал, на шар, имеющий меньший потенциал, до тех пор, пока потенциалы шаров не станут одинаковми:

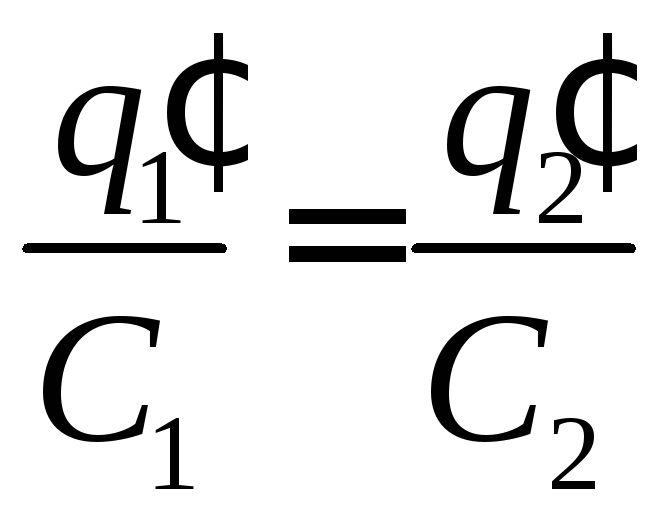= ; (86)

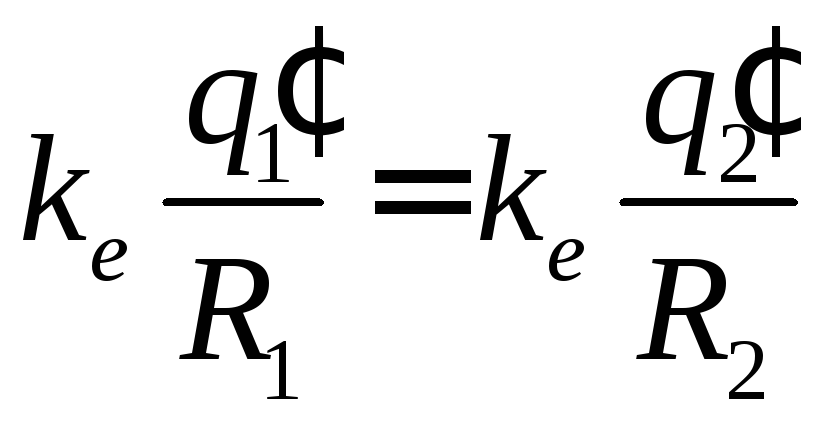; (87)

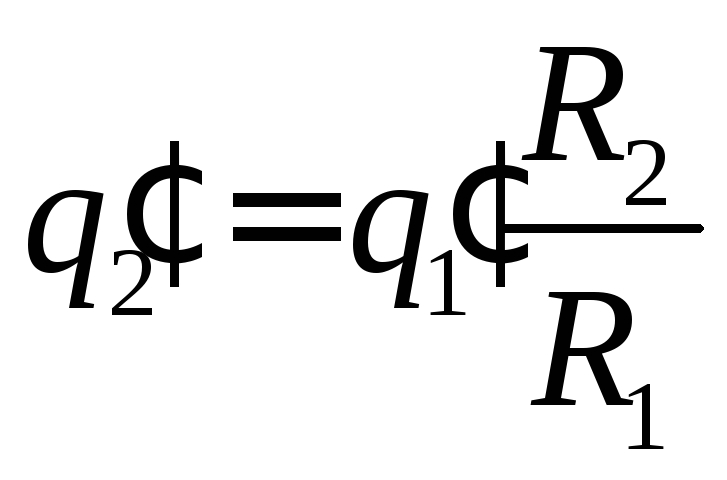. (88)

Заряд первого шара после соединения шаров определим из уравнения энергии:

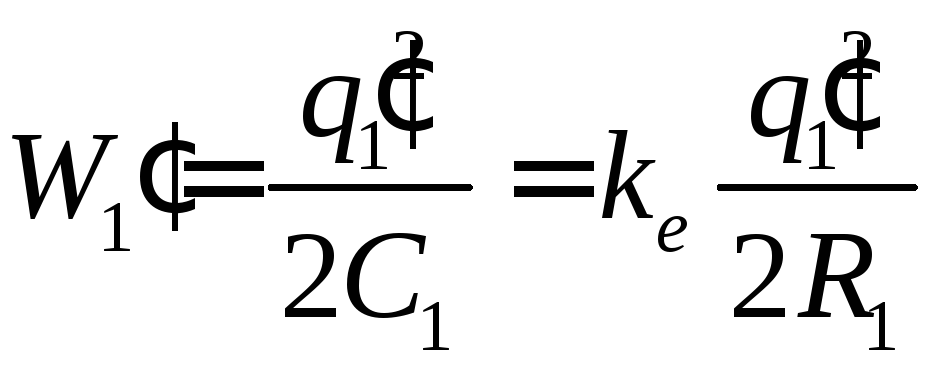; (89)

. (90)

Величину заряда первого шара до соприкосновения можно найти из закона сохранения заряда:

q₁ + q₂ = q'₁ + q'₂; (91)

q₁ = q'₁ + q'₂  q₂ = q'₁ +  = q'₁ =

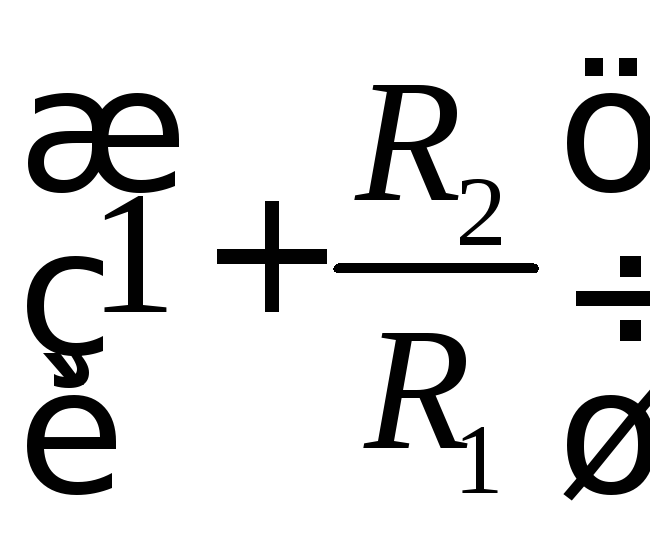
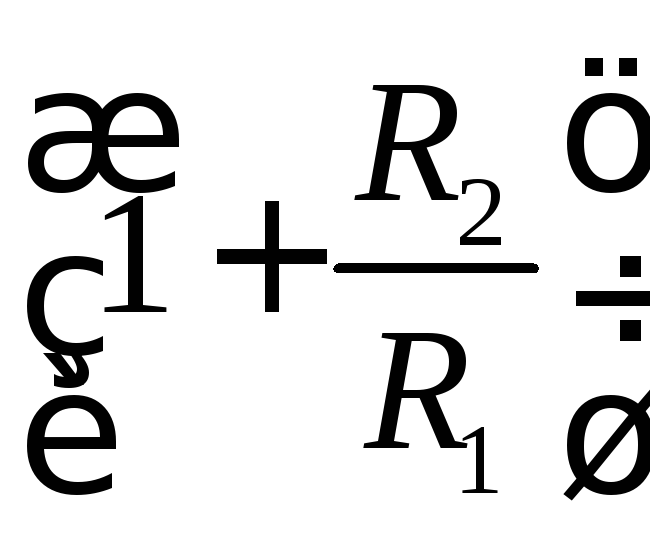
 . (92)

Вычислим величину q₁, подставив данные задачи:

q₁ = 1,3610^7 Кл.

Далее вычислим энергию первого и второго шара до разряда, а также заряд второго шара после соприкосновения:

W₁ = ; W₁ = 9,810^3 Дж;

W₂ = ; W₂ = 2,010^5 Дж;

q'₂ 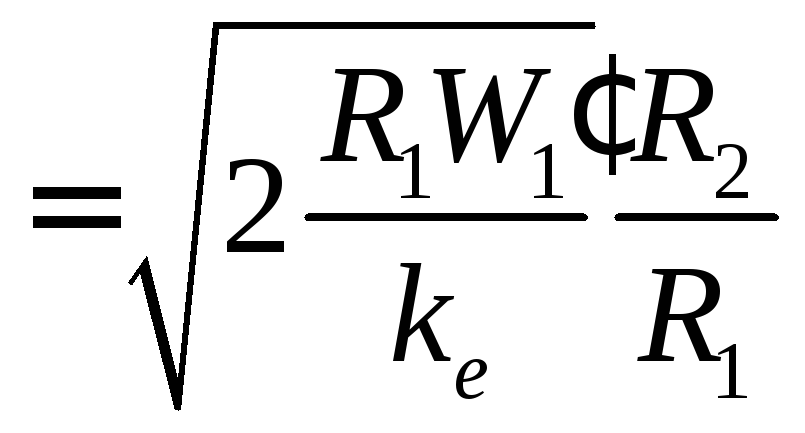;q'₂ = 1,5410^7 Кл.

Работу разряда найдем как разность энергий двух шаров до и после их соединения:

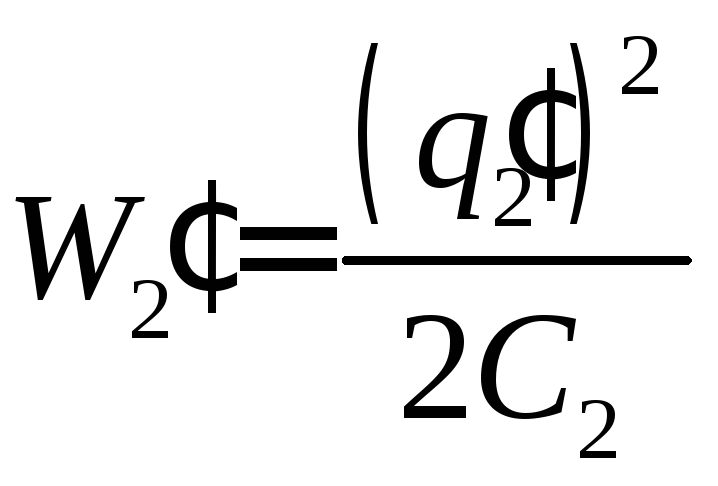; = 2,710^3 Дж;

А = (W₁ + W₂)  ( + ); А = 5,1210^3 Дж.

Ответ:W₁ = 9,810^3 Дж; W₂ = 2,010^5 Дж; А = 5,1210^3 Дж;q₁ = 1,3610^7 Кл;q'₂ = 1,5410^7 Кл.

Задача 12. Плоский воздушный конденсатор с площадью пластин 8 дм² и расстоянием между ними 2 мм соединили с источником напряжения, и на обкладках конденсатора появился заряд 5 нКл. На сколько изменится энергия конденсатора, если в него ввести диэлектрик с диэлектрической проницаемостью, равной четырем: 1) не отключая конденсатор от источника напряжения; 2) отключив предварительно конденсатор от источника напряжения.

Дано: S = 8 дм2 = 8102 м2 d = 2 мм = 2103 м q = 5 нКл = 5109 Кл 1 = 1 2 = 4

Найти: W1, W2.

Решение. 1) Если конденсатор соединен с источником напряжения, то при введении в него диэлектрика разность потенциалов между пластинами не изменяется, т. е.  = const, а меняется электроемкость конденсатора: C₁ = ; C₂ = .

Энергию конденсатора до и после введения диэлектрика в этом случае удобнее выражать через разность потенциалов:

W₁ = 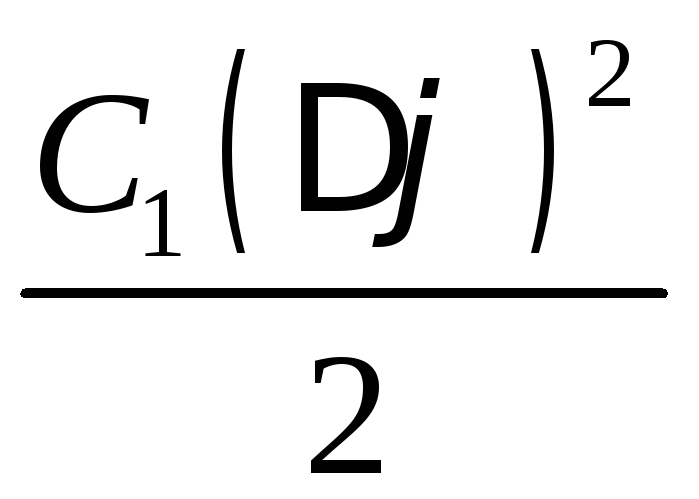; (93)

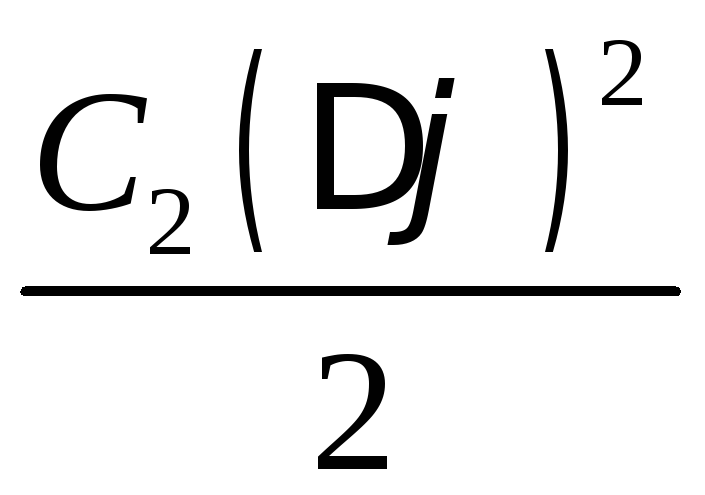W₂ = . (94)

Так как C₂ > С₁, то W₂ > W₁ – энергия конденсатора увеличивается, тогда

W₁ = W₂ – W₁ = 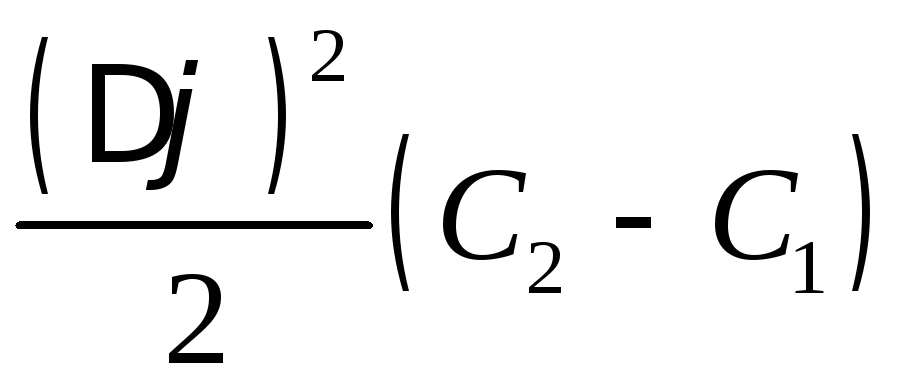. (95)

Разность потенциалов между пластинами конденсатора можно найти через его заряд q и емкость С₁:

 = q/C₁; (96)

W₁ = 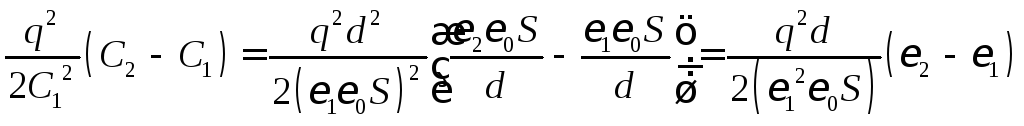. (97)

Подставив данные задачи, получим: W₁ = 10^5 Дж.

2) При отключении конденсатора от источника напряжения сообщенный ему заряд не меняется: q = const. Энергию конденсатора удобнее выражать через заряд:

W₁ = ; (98)

W₂ = . (99)

Если C₂ > С₁, то W₂ < W₁ – энергия конденсатора уменьшается, тогда

W₂ = 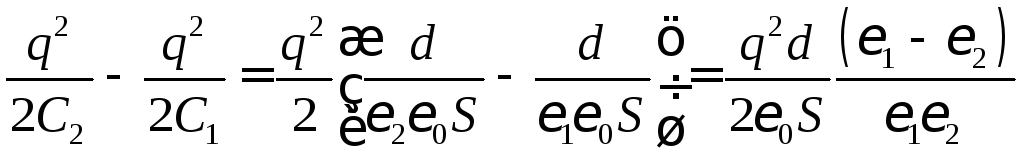. (100)

Подставляя численные значения, получим: W₂ = 2,510^6 Дж.

Ответ:W₁ = 10^5 Дж;W₂ = 2,510^6 Дж.