
- •Введение
- •1. Частота и период свободных незатухающих колебаний
- •1.1. Основные формулы и обозначения
- •1.2. Примеры решения задач
- •2. Свободные незатухающие механические колебания
- •2.1. Основные формулы и обозначения
- •2.2. Примеры решения задач
- •3. Свободные незатухающие колебания в идеальном колебательном контуре
- •3.1. Основные формулы и обозначения
- •3.2. Примеры решения задач
- •4. Сложение гармонических колебаний
- •4.1. Основные формулы и обозначения
- •4.2. Примеры решения задач
- •5. Свободные затухающие механические колебания
- •5.1. Основные формулы и обозначения
- •5.2. Примеры решения задач
- •6. Свободные затухающие колебания в реальном колебательном контуре
- •6.1. Основные формулы и обозначения
- •6.2. Примеры решения задач
- •7. Вынужденные механические колебания1
- •7.1. Основные формулы и обозначения
- •7.2. Примеры решения задач
- •8. Вынужденные колебания в колебательном контуре. Резонанс. Импеданс1
- •8.1. Основные формулы и обозначения
- •8.2. Примеры решения задач
- •9. Плоские монохроматические
- •9.1. Основные формулы и обозначения
- •9.2. Примеры решения задач
- •Библиографический список
- •644046, Г. Омск, пр. Маркса, 35
8.2. Примеры решения задач
З а д а ч а 18. К
источнику переменного напряжения,
меняющегося по закону
![]() где
где![]() В,
В,![]() с-1,
последовательно подключены конденсатор
емкостью 120 мкФ, катушка индуктивностью
0,34 мГн и резистор сопротивлением 180 Ом
(см. рис. 10). Найти законы изменения заряда
и силы тока в цепи.
с-1,
последовательно подключены конденсатор
емкостью 120 мкФ, катушка индуктивностью
0,34 мГн и резистор сопротивлением 180 Ом
(см. рис. 10). Найти законы изменения заряда
и силы тока в цепи.
|
Дано:
Найти:
|
Решение. Законы установившихся вынужденных колебаний заряда и силы тока в цепи имеют вид:
Амплитуда колебаний силы тока
|
где
![]() – модуль импеданса.
– модуль импеданса.
Разность фаз
![]() колебаний заряда и вынуждающей
электродвижущей силы вычисляется по
формуле:
колебаний заряда и вынуждающей
электродвижущей силы вычисляется по
формуле:
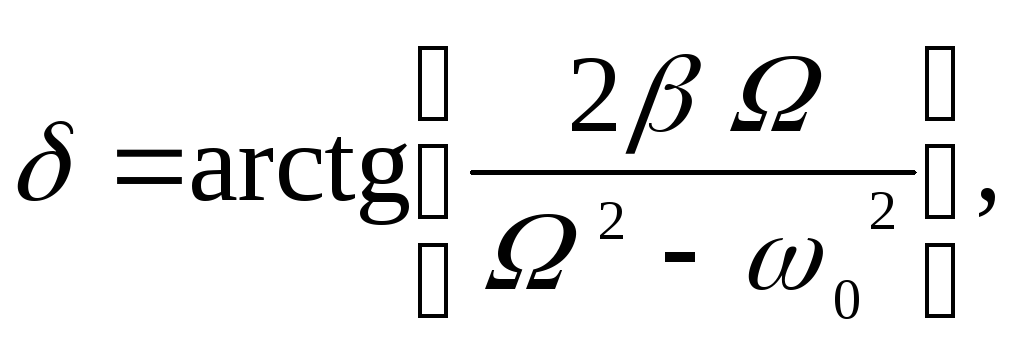
![]() (138)
(138)
где
![]() – (139)
– (139)
собственная частота колебаний в контуре;
![]() – (140)
– (140)
коэффициент затухания.
Комбинируя выражения (137) – (140), получим:
 (141)
(141)
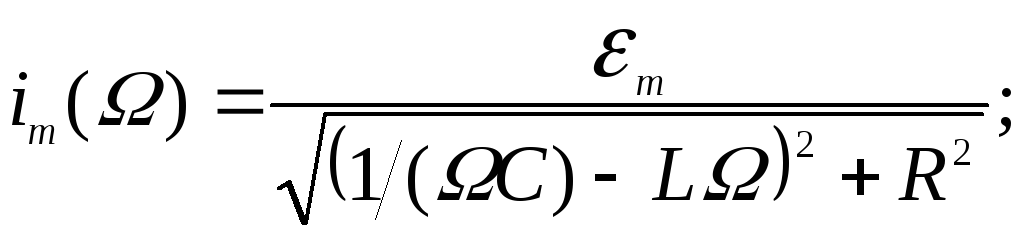 (142)
(142)
![]()
![]() (143)
(143)
Подставляем в
выражения (141) – (143) численные данные:
![]() мКл;
мКл;
![]() А;
А;
![]() °.
°.
Ответ:
![]() где
где![]() мКл,
мКл,![]() °;
°;
![]() где
где
![]() А,
А,![]() °.
°.
З а д а ч а 19. Найти добротность колебательного контура, если резонанс напряжения на обкладках конденсатора, входящего в контур, наблюдается при частоте, в 1,0008 раза меньшей частоты затухающих колебаний в этом контуре.
|
Дано:
Найти:
|
Решение. Напряжение
на обкладках конденсатора
|
Резонансная частота вынужденных колебаний определяется по формуле (121):
![]() (144)
(144)
где
![]() – собственная частота колебаний в
контуре;
– собственная частота колебаний в
контуре;
![]() –коэффициент
затухания.
–коэффициент
затухания.
Соотношение для частоты затухающих колебаний имеет вид:
![]() (145)
(145)
Выражения (144) и
(145) позволяют найти отношение
![]() .
Если
.
Если![]() ,
то затухание можно считать малым. Тогда
для определения добротности можно
применить формулу:
,
то затухание можно считать малым. Тогда
для определения добротности можно
применить формулу:
![]() (146)
(146)
Возведем соотношения
(144) и (145) в квадрат:
![]() ;
;![]() .
Отсюда
.
Отсюда
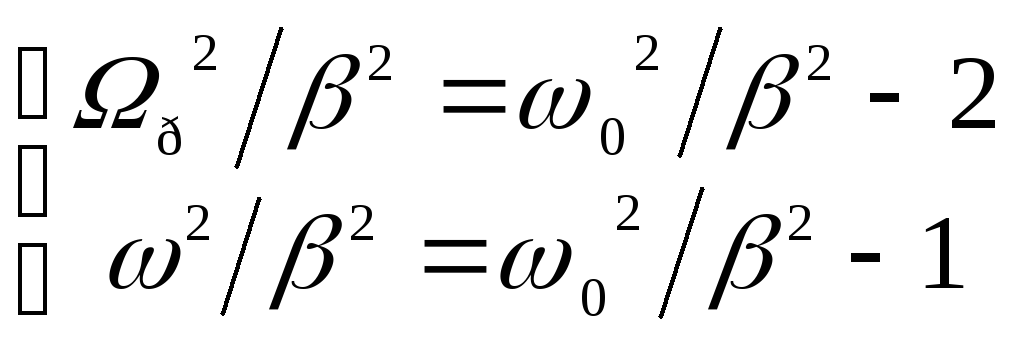 .
(147)
.
(147)
С учетом отношения левых частей равенств (147)
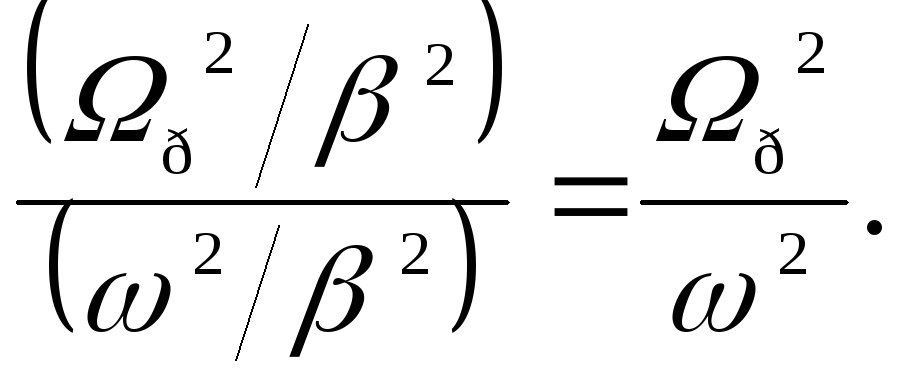 (148)
(148)
отношение правых
частей равенств (147) принимает вид:
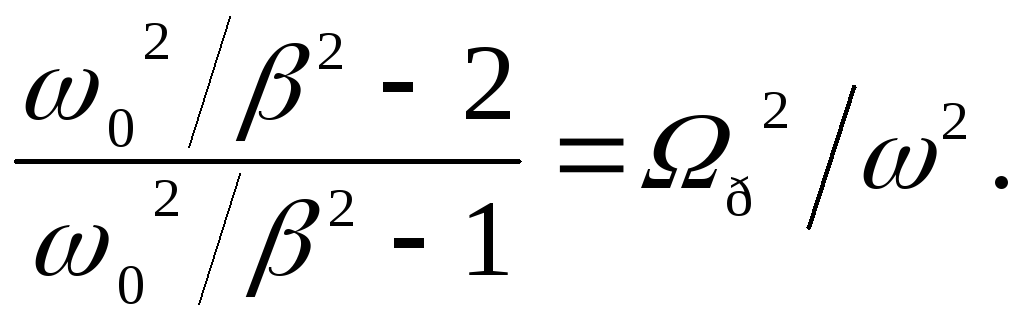 Отсюда
Отсюда
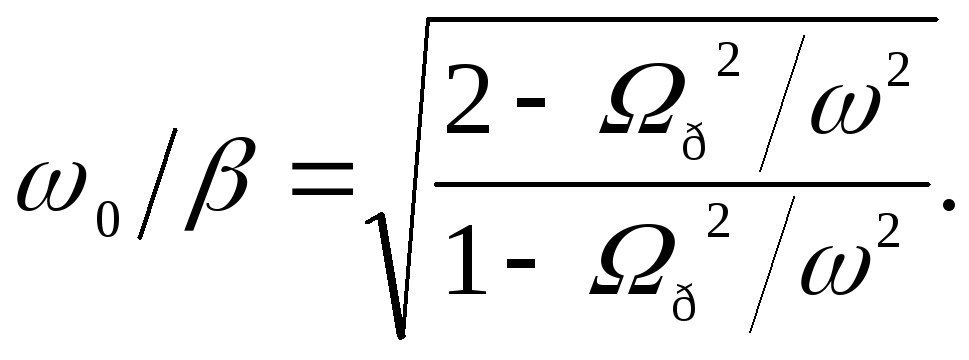 (149)
(149)
Подставляя в выражение (149) численные данные, получим:
![]()
Следовательно,
![]() ,
поэтому формула (146) применима. Подставляя
в формулу (146) соотношение (149), получим:
,
поэтому формула (146) применима. Подставляя
в формулу (146) соотношение (149), получим:
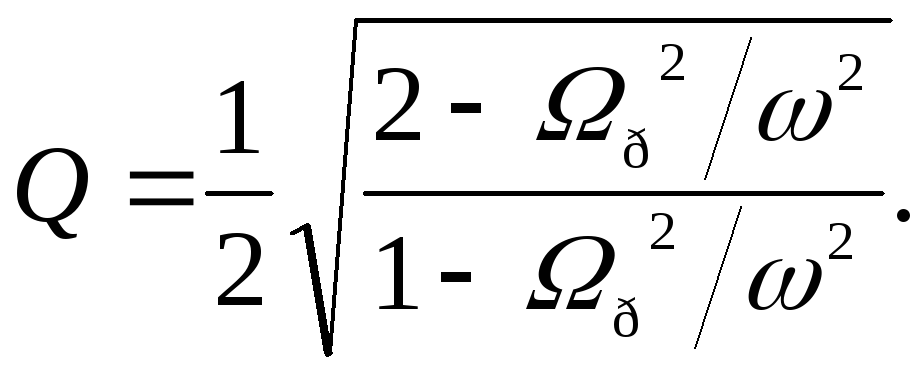 (150)
(150)
Используем численные данные:
![]()
Ответ:
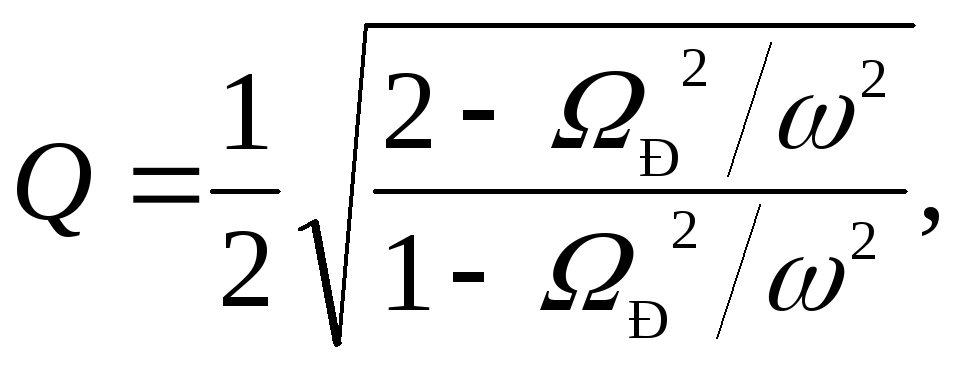
![]()
9. Плоские монохроматические
УПРУГИЕ И ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
9.1. Основные формулы и обозначения
Пусть плоская
монохроматическая (гармоническая) волна
с длиной
![]() и периодом
и периодом
![]() распространяется
в направлении оси
распространяется
в направлении оси
![]() с (фазовой) скоростью
с (фазовой) скоростью
![]() Тогда уравнение, описывающее колебания
точек такой волны (уравнение бегущей
волны), имеет вид:
Тогда уравнение, описывающее колебания
точек такой волны (уравнение бегущей
волны), имеет вид:
![]() (151)
(151)
где
![]() – смещение колеблющейся точки волны
от положения равновесия;
– смещение колеблющейся точки волны
от положения равновесия;
![]() –координата
колеблющейся точки;
–координата
колеблющейся точки;
![]() –амплитуда;
–амплитуда;
![]() –фаза волны;
–фаза волны;
![]() –круговая частота;
–круговая частота;
![]() –волновое число
(модуль волнового вектора
–волновое число
(модуль волнового вектора
![]() ,
,![]() ).
).
Разность фаз
гармонической волны в двух точках с
координатами
![]() и
и![]()
![]() . (152)
. (152)
Пусть плоская
монохроматическая электромагнитная
волна, распространяется в направлении
оси
![]() в однородной изотропной среде вдали
от зарядов и токов, создающих
электромагнитное поле. Тогда
направления колебаний напряженностей
электрического
в однородной изотропной среде вдали
от зарядов и токов, создающих
электромагнитное поле. Тогда
направления колебаний напряженностей
электрического![]() и магнитного
и магнитного![]() полей в любой момент времени
перпендикулярны направлению
распространения волны:
полей в любой момент времени
перпендикулярны направлению
распространения волны:![]() и
и![]() и, кроме того, взаимно перпендикулярны:
и, кроме того, взаимно перпендикулярны:![]() (рис. 11). Законы колебаний ненулевых
проекций векторов
(рис. 11). Законы колебаний ненулевых
проекций векторов![]() и
и![]() во всех точках с координатой
во всех точках с координатой![]() имеют вид:
имеют вид:![]() ;
;![]() и с
и с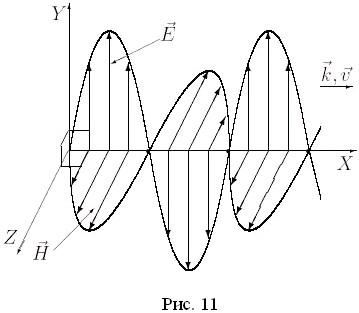 вязаны
между собой соотношением:
вязаны
между собой соотношением:![]() ,
где
,
где![]() и
и![]() – соответственно магнитная и электрическая
проницаемость среды;
– соответственно магнитная и электрическая
проницаемость среды;![]() и
и![]() – магнитная и электрическая постоянные.
Аналогичное соотношение справедливо
и для амплитуд
– магнитная и электрическая постоянные.
Аналогичное соотношение справедливо
и для амплитуд![]() ,
,![]() колебаний напряженностей:
колебаний напряженностей:![]() .
Частоты и фазы колебаний напряженности
Рис. 11
.
Частоты и фазы колебаний напряженности
Рис. 11
электрического и
магнитного полей плоской монохроматической
электромагнитной волны одинаковы в
любой момент времени. Максимальная
скорость распространения электромагнитных
волн – их скорость в вакууме, равная
скорости света в вакууме:
![]() м/с. Скорость их распространения в
однородной изотропной среде
м/с. Скорость их распространения в
однородной изотропной среде![]() .
.

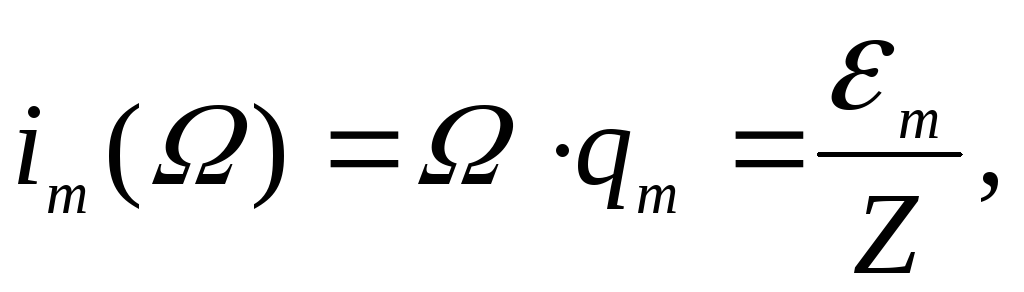 (137)
(137)